
Previous in Relation and Functions Next in Relation and Functions
Question Number 90969 by abdomathmax last updated on 27/Apr/20
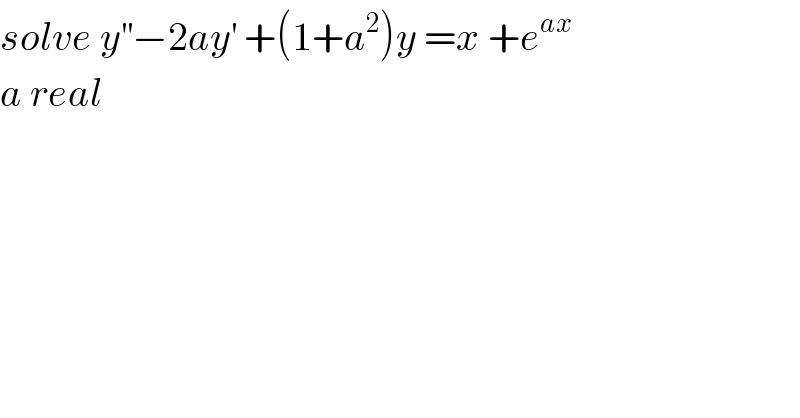
$${solve}\:{y}^{''} −\mathrm{2}{ay}^{'} \:+\left(\mathrm{1}+{a}^{\mathrm{2}} \right){y}\:={x}\:+{e}^{{ax}} \\ $$$${a}\:{real} \\ $$
Commented by niroj last updated on 27/Apr/20
![y^(′′) −2ay^′ +(1+a^2 )y=x +e^(ax) (D^2 −2aD+1+a^2 )y= x+e^(ax) A.E., m^2 −2am+(1+a^2 )=0 m= ((2a+^− (√(4a^2 −4(1+a^2 ))))/2) = ((2a+^− (√(4a^2 −4−4a^2 )))/2)= ((2a+^− (√(−4)))/2) m= a+^− i CF= e^(ax) (C_1 cos x+C_2 sinx) PI= ((x+e^(ax) )/(D^2 −2aD+(1+a^2 ))) = (1/(1+a^2 ))[ (1/(1+((D^2 −2aD)/(1+a^2 ))))]x+ (e^(ax) /(a^2 −2a^2 +1+a^2 )) = (1/(1+a^2 ))(1+((D^2 −2aD)/(1+a^2 )))^(−1) x+ (e^(ax) /1) = (1/(1+a^2 ))[ 1−(((D^2 −2aD)/(1+a^2 )))+(((D^2 −2aD)/(1+a^2 )))^2 −...]x + e^(ax) = (1/(1+a^2 ))[ 1+((2aD)/(1+a^2 ))]x+e^(ax) = (1/(1+a^2 ))[ x +((2a)/(1+a^2 ))Dx]+e^(ax) = (1/(1+a^2 ))[x+((2a)/(1+a^2 ))]+e^(ax) y=CF+PI y= e^(ax) (C_1 cosx+C_2 sinx)+ (x/(1+a^2 ))+((2a)/((1+a^2 )^2 ))+e^(ax) //.](Q91072.png)
$$\:\mathrm{y}^{''} −\mathrm{2ay}^{'} +\left(\mathrm{1}+\mathrm{a}^{\mathrm{2}} \right)\mathrm{y}=\mathrm{x}\:+\mathrm{e}^{\mathrm{ax}} \\ $$$$\:\:\:\left(\mathrm{D}^{\mathrm{2}} −\mathrm{2aD}+\mathrm{1}+\mathrm{a}^{\mathrm{2}} \right)\mathrm{y}=\:\mathrm{x}+\mathrm{e}^{\mathrm{ax}} \\ $$$$\:\:\mathrm{A}.\mathrm{E}., \\ $$$$\:\mathrm{m}^{\mathrm{2}} −\mathrm{2am}+\left(\mathrm{1}+\mathrm{a}^{\mathrm{2}} \right)=\mathrm{0} \\ $$$$\:\:\mathrm{m}=\:\frac{\mathrm{2a}\overset{−} {+}\sqrt{\mathrm{4a}^{\mathrm{2}} −\mathrm{4}\left(\mathrm{1}+\mathrm{a}^{\mathrm{2}} \right)}}{\mathrm{2}} \\ $$$$\:\:\:\:=\:\frac{\mathrm{2a}\overset{−} {+}\sqrt{\mathrm{4a}^{\mathrm{2}} −\mathrm{4}−\mathrm{4a}^{\mathrm{2}} }}{\mathrm{2}}=\:\frac{\mathrm{2a}\overset{−} {+}\sqrt{−\mathrm{4}}}{\mathrm{2}} \\ $$$$\:\mathrm{m}=\:\mathrm{a}\overset{−} {+}\mathrm{i} \\ $$$$\:\mathrm{CF}=\:\mathrm{e}^{\mathrm{ax}} \left(\mathrm{C}_{\mathrm{1}} \mathrm{cos}\:\mathrm{x}+\mathrm{C}_{\mathrm{2}} \mathrm{sinx}\right) \\ $$$$\:\mathrm{PI}=\:\frac{\mathrm{x}+\mathrm{e}^{\mathrm{ax}} }{\mathrm{D}^{\mathrm{2}} −\mathrm{2}{a}\mathrm{D}+\left(\mathrm{1}+\mathrm{a}^{\mathrm{2}} \right)} \\ $$$$\:=\:\frac{\mathrm{1}}{\mathrm{1}+\mathrm{a}^{\mathrm{2}} }\left[\:\frac{\mathrm{1}}{\mathrm{1}+\frac{\mathrm{D}^{\mathrm{2}} −\mathrm{2aD}}{\mathrm{1}+\mathrm{a}^{\mathrm{2}} }}\right]\mathrm{x}+\:\frac{\mathrm{e}^{\mathrm{ax}} }{\mathrm{a}^{\mathrm{2}} −\mathrm{2a}^{\mathrm{2}} +\mathrm{1}+\mathrm{a}^{\mathrm{2}} } \\ $$$$=\:\frac{\mathrm{1}}{\mathrm{1}+\mathrm{a}^{\mathrm{2}} }\left(\mathrm{1}+\frac{\mathrm{D}^{\mathrm{2}} −\mathrm{2aD}}{\mathrm{1}+\mathrm{a}^{\mathrm{2}} }\right)^{−\mathrm{1}} \mathrm{x}+\:\frac{\mathrm{e}^{\mathrm{ax}} }{\mathrm{1}} \\ $$$$=\:\frac{\mathrm{1}}{\mathrm{1}+\mathrm{a}^{\mathrm{2}} }\left[\:\mathrm{1}−\left(\frac{\mathrm{D}^{\mathrm{2}} −\mathrm{2aD}}{\mathrm{1}+\mathrm{a}^{\mathrm{2}} }\right)+\left(\frac{\mathrm{D}^{\mathrm{2}} −\mathrm{2aD}}{\mathrm{1}+\mathrm{a}^{\mathrm{2}} }\right)^{\mathrm{2}} −...\right]\mathrm{x}\:+\:\mathrm{e}^{\mathrm{ax}} \\ $$$$\:=\:\frac{\mathrm{1}}{\mathrm{1}+\mathrm{a}^{\mathrm{2}} }\left[\:\mathrm{1}+\frac{\mathrm{2aD}}{\mathrm{1}+\mathrm{a}^{\mathrm{2}} }\right]\mathrm{x}+\mathrm{e}^{\mathrm{ax}} \\ $$$$=\:\frac{\mathrm{1}}{\mathrm{1}+\mathrm{a}^{\mathrm{2}} }\left[\:\mathrm{x}\:+\frac{\mathrm{2a}}{\mathrm{1}+\mathrm{a}^{\mathrm{2}} }\mathrm{Dx}\right]+\mathrm{e}^{\mathrm{ax}} \\ $$$$=\:\frac{\mathrm{1}}{\mathrm{1}+\mathrm{a}^{\mathrm{2}} }\left[\mathrm{x}+\frac{\mathrm{2a}}{\mathrm{1}+\mathrm{a}^{\mathrm{2}} }\right]+\mathrm{e}^{\mathrm{ax}} \\ $$$$\:\mathrm{y}=\mathrm{CF}+\mathrm{PI} \\ $$$$\:\mathrm{y}=\:\mathrm{e}^{\mathrm{ax}} \left(\mathrm{C}_{\mathrm{1}} \mathrm{cosx}+\mathrm{C}_{\mathrm{2}} \mathrm{sinx}\right)+\:\frac{\mathrm{x}}{\mathrm{1}+\mathrm{a}^{\mathrm{2}} }+\frac{\mathrm{2a}}{\left(\mathrm{1}+\mathrm{a}^{\mathrm{2}} \right)^{\mathrm{2}} }+\mathrm{e}^{\mathrm{ax}} \://. \\ $$
Commented by mathmax by abdo last updated on 28/Apr/20

$${thank}\:{you}\:{sir}. \\ $$
Commented by niroj last updated on 03/May/20
��
