Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 166378 by MathsFan last updated on 19/Feb/22

8x^3 −6x+1=0 solve for x

$$\:\mathrm{8}{x}^{\mathrm{3}} −\mathrm{6}{x}+\mathrm{1}=\mathrm{0} \\ $$$$\:{solve}\:{for}\:{x} \\ $$

Answered by mr W last updated on 19/Feb/22

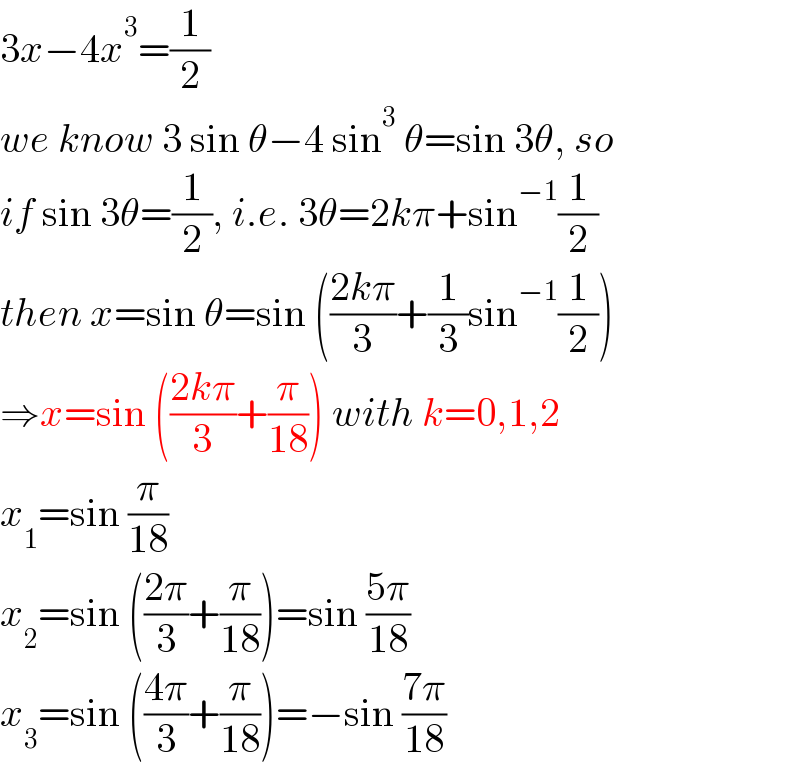
3x−4x^3 =(1/2) we know 3 sin θ−4 sin^3 θ=sin 3θ, so if sin 3θ=(1/2), i.e. 3θ=2kπ+sin^(−1) (1/2) then x=sin θ=sin (((2kπ)/3)+(1/3)sin^(−1) (1/2)) ⇒x=sin (((2kπ)/3)+(π/(18))) with k=0,1,2 x_1 =sin (π/(18)) x_2 =sin (((2π)/3)+(π/(18)))=sin ((5π)/(18)) x_3 =sin (((4π)/3)+(π/(18)))=−sin ((7π)/(18))

$$\mathrm{3}{x}−\mathrm{4}{x}^{\mathrm{3}} =\frac{\mathrm{1}}{\mathrm{2}} \\ $$$${we}\:{know}\:\mathrm{3}\:\mathrm{sin}\:\theta−\mathrm{4}\:\mathrm{sin}^{\mathrm{3}} \:\theta=\mathrm{sin}\:\mathrm{3}\theta,\:{so} \\ $$$${if}\:\mathrm{sin}\:\mathrm{3}\theta=\frac{\mathrm{1}}{\mathrm{2}},\:{i}.{e}.\:\mathrm{3}\theta=\mathrm{2}{k}\pi+\mathrm{sin}^{−\mathrm{1}} \frac{\mathrm{1}}{\mathrm{2}} \\ $$$${then}\:{x}=\mathrm{sin}\:\theta=\mathrm{sin}\:\left(\frac{\mathrm{2}{k}\pi}{\mathrm{3}}+\frac{\mathrm{1}}{\mathrm{3}}\mathrm{sin}^{−\mathrm{1}} \frac{\mathrm{1}}{\mathrm{2}}\right) \\ $$$$\Rightarrow{x}=\mathrm{sin}\:\left(\frac{\mathrm{2}{k}\pi}{\mathrm{3}}+\frac{\pi}{\mathrm{18}}\right)\:{with}\:{k}=\mathrm{0},\mathrm{1},\mathrm{2} \\ $$$${x}_{\mathrm{1}} =\mathrm{sin}\:\frac{\pi}{\mathrm{18}} \\ $$$${x}_{\mathrm{2}} =\mathrm{sin}\:\left(\frac{\mathrm{2}\pi}{\mathrm{3}}+\frac{\pi}{\mathrm{18}}\right)=\mathrm{sin}\:\frac{\mathrm{5}\pi}{\mathrm{18}} \\ $$$${x}_{\mathrm{3}} =\mathrm{sin}\:\left(\frac{\mathrm{4}\pi}{\mathrm{3}}+\frac{\pi}{\mathrm{18}}\right)=−\mathrm{sin}\:\frac{\mathrm{7}\pi}{\mathrm{18}} \\ $$

Commented by MathsFan last updated on 19/Feb/22

thank you sir but can canado′s formula be applied to this question?

$${thank}\:{you}\:{sir} \\ $$$${but}\:{can}\:{canado}'{s}\:{formula}\:{be}\:{applied} \\ $$$${to}\:{this}\:{question}? \\ $$

Commented by mr W last updated on 19/Feb/22

no.

$${no}. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com