
Question Number 88569 by M±th+et£s last updated on 11/Apr/20
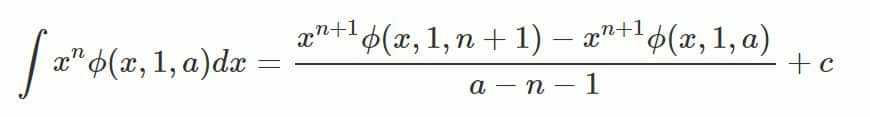
Commented by M±th+et£s last updated on 11/Apr/20

$${prove}\:{that} \\ $$$$ \\ $$$$\because\emptyset\:{lerch}\:{transcendent} \\ $$
Answered by mind is power last updated on 12/Apr/20
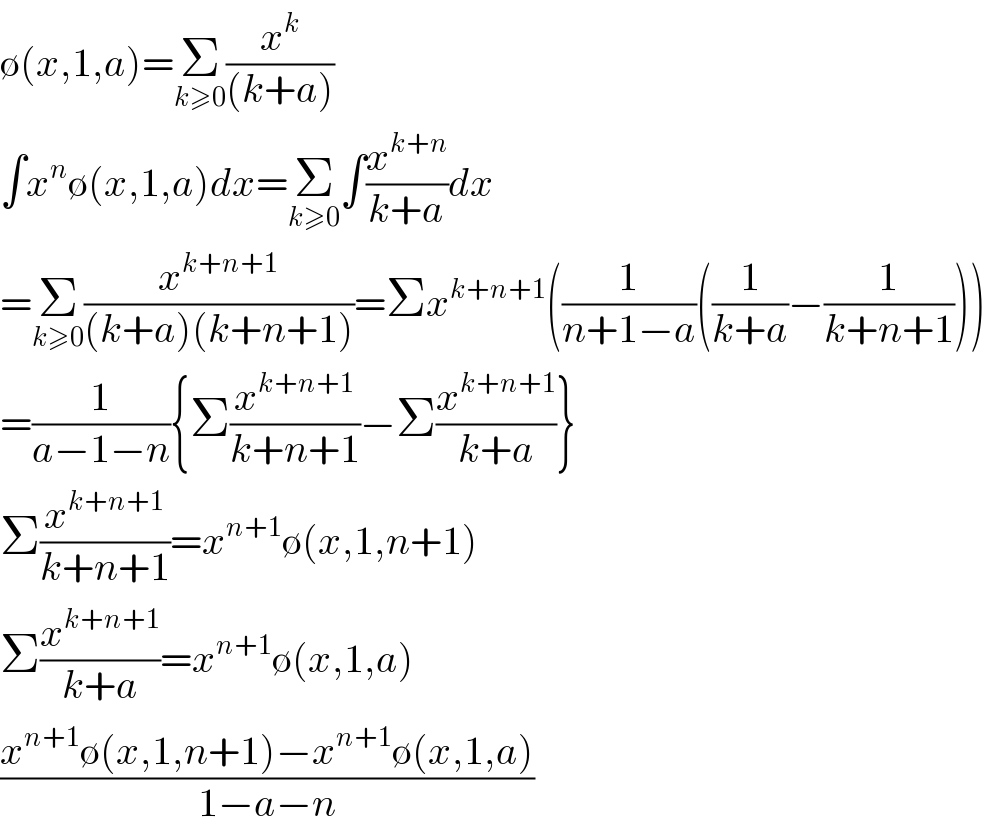
$$\emptyset\left({x},\mathrm{1},{a}\right)=\underset{{k}\geqslant\mathrm{0}} {\sum}\frac{{x}^{{k}} }{\left({k}+{a}\right)} \\ $$$$\int{x}^{{n}} \emptyset\left({x},\mathrm{1},{a}\right){dx}=\underset{{k}\geqslant\mathrm{0}} {\sum}\int\frac{{x}^{{k}+{n}} }{{k}+{a}}{dx} \\ $$$$=\underset{{k}\geqslant\mathrm{0}} {\sum}\frac{{x}^{{k}+{n}+\mathrm{1}} }{\left({k}+{a}\right)\left({k}+{n}+\mathrm{1}\right)}=\Sigma{x}^{{k}+{n}+\mathrm{1}} \left(\frac{\mathrm{1}}{{n}+\mathrm{1}−{a}}\left(\frac{\mathrm{1}}{{k}+{a}}−\frac{\mathrm{1}}{{k}+{n}+\mathrm{1}}\right)\right) \\ $$$$=\frac{\mathrm{1}}{{a}−\mathrm{1}−{n}}\left\{\Sigma\frac{{x}^{{k}+{n}+\mathrm{1}} }{{k}+{n}+\mathrm{1}}−\Sigma\frac{{x}^{{k}+{n}+\mathrm{1}} }{{k}+{a}}\right\} \\ $$$$\Sigma\frac{{x}^{{k}+{n}+\mathrm{1}} }{{k}+{n}+\mathrm{1}}={x}^{{n}+\mathrm{1}} \emptyset\left({x},\mathrm{1},{n}+\mathrm{1}\right) \\ $$$$\Sigma\frac{{x}^{{k}+{n}+\mathrm{1}} }{{k}+{a}}={x}^{{n}+\mathrm{1}} \emptyset\left({x},\mathrm{1},{a}\right) \\ $$$$\frac{{x}^{{n}+\mathrm{1}} \emptyset\left({x},\mathrm{1},{n}+\mathrm{1}\right)−{x}^{{n}+\mathrm{1}} \emptyset\left({x},\mathrm{1},{a}\right)}{\mathrm{1}−{a}−{n}} \\ $$
Commented by M±th+et£s last updated on 12/Apr/20

$${great}\:{solution}\: \\ $$
