
Question Number 87755 by john santu last updated on 06/Apr/20
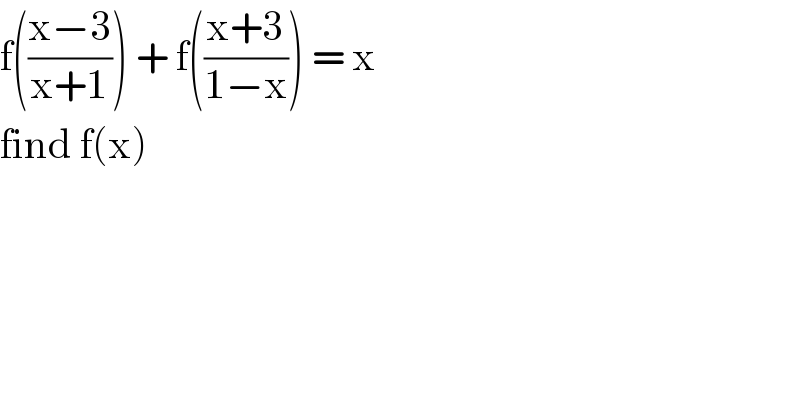
$$\mathrm{f}\left(\frac{\mathrm{x}−\mathrm{3}}{\mathrm{x}+\mathrm{1}}\right)\:+\:\mathrm{f}\left(\frac{\mathrm{x}+\mathrm{3}}{\mathrm{1}−\mathrm{x}}\right)\:=\:\mathrm{x} \\ $$$$\mathrm{find}\:\mathrm{f}\left(\mathrm{x}\right) \\ $$
Commented by john santu last updated on 06/Apr/20
![(i) let ((x−3)/(x+1)) = x′ ⇒f(x′) + f(((x′−3)/(x′+1))) = ((x′+3)/(1−x)) (ii) let ((x+3)/(1−x)) = x′⇒ f(((x′+3)/(1−x′))) +f(x′) = ((x′−3)/(x′+1)) eq +(i)+(ii) 2 [ f(((x−3)/(x+1)))+f(((x+3)/(1−x)))+f(x) ] = x+((x+3)/(1−x))+((x−3)/(x+1)) 2 [ x +f(x) ] = ((x(1−x^2 )+x^2 +4x+3−x^2 +4x−3)/(1−x^2 )) 2 [ x+f(x) ] = ((−x^3 +9x)/(1−x^2 )) f(x) = ((9x−x^3 )/(2−2x^2 )) − ((x(2−2x^2 ))/(2−2x^2 )) f(x) = ((x^3 +7x)/(2−2x^2 )) .](Q87756.png)
$$\left(\mathrm{i}\right)\:\mathrm{let}\:\frac{\mathrm{x}−\mathrm{3}}{\mathrm{x}+\mathrm{1}}\:=\:\mathrm{x}'\:\Rightarrow\mathrm{f}\left(\mathrm{x}'\right)\:+\:\mathrm{f}\left(\frac{\mathrm{x}'−\mathrm{3}}{\mathrm{x}'+\mathrm{1}}\right)\:=\:\frac{\mathrm{x}'+\mathrm{3}}{\mathrm{1}−\mathrm{x}} \\ $$$$\left(\mathrm{ii}\right)\:\mathrm{let}\:\frac{\mathrm{x}+\mathrm{3}}{\mathrm{1}−\mathrm{x}}\:=\:\mathrm{x}'\Rightarrow\:\mathrm{f}\left(\frac{\mathrm{x}'+\mathrm{3}}{\mathrm{1}−\mathrm{x}'}\right)\:+\mathrm{f}\left(\mathrm{x}'\right)\:=\:\frac{\mathrm{x}'−\mathrm{3}}{\mathrm{x}'+\mathrm{1}} \\ $$$$\mathrm{eq}\:+\left(\mathrm{i}\right)+\left(\mathrm{ii}\right) \\ $$$$\mathrm{2}\:\left[\:\mathrm{f}\left(\frac{\mathrm{x}−\mathrm{3}}{\mathrm{x}+\mathrm{1}}\right)+\mathrm{f}\left(\frac{\mathrm{x}+\mathrm{3}}{\mathrm{1}−\mathrm{x}}\right)+\mathrm{f}\left(\mathrm{x}\right)\:\right]\:=\:\mathrm{x}+\frac{\mathrm{x}+\mathrm{3}}{\mathrm{1}−\mathrm{x}}+\frac{\mathrm{x}−\mathrm{3}}{\mathrm{x}+\mathrm{1}} \\ $$$$\mathrm{2}\:\left[\:\mathrm{x}\:+\mathrm{f}\left(\mathrm{x}\right)\:\right]\:=\:\frac{\mathrm{x}\left(\mathrm{1}−\mathrm{x}^{\mathrm{2}} \right)+\mathrm{x}^{\mathrm{2}} +\mathrm{4x}+\mathrm{3}−\mathrm{x}^{\mathrm{2}} +\mathrm{4x}−\mathrm{3}}{\mathrm{1}−\mathrm{x}^{\mathrm{2}} } \\ $$$$\mathrm{2}\:\left[\:\mathrm{x}+\mathrm{f}\left(\mathrm{x}\right)\:\right]\:=\:\frac{−\mathrm{x}^{\mathrm{3}} +\mathrm{9x}}{\mathrm{1}−\mathrm{x}^{\mathrm{2}} } \\ $$$$\mathrm{f}\left(\mathrm{x}\right)\:=\:\frac{\mathrm{9x}−\mathrm{x}^{\mathrm{3}} }{\mathrm{2}−\mathrm{2x}^{\mathrm{2}} }\:−\:\frac{\mathrm{x}\left(\mathrm{2}−\mathrm{2x}^{\mathrm{2}} \right)}{\mathrm{2}−\mathrm{2x}^{\mathrm{2}} } \\ $$$$\mathrm{f}\left(\mathrm{x}\right)\:=\:\frac{\mathrm{x}^{\mathrm{3}} +\mathrm{7x}}{\mathrm{2}−\mathrm{2x}^{\mathrm{2}} }\:.\: \\ $$
Commented by jagoll last updated on 06/Apr/20
$$\mathrm{thank}\:\mathrm{you}\:\mathrm{mister}.\:\mathrm{ilike} \\ $$$$\mathrm{this}\:\mathrm{question} \\ $$
