
Question Number 87751 by Rio Michael last updated on 06/Apr/20
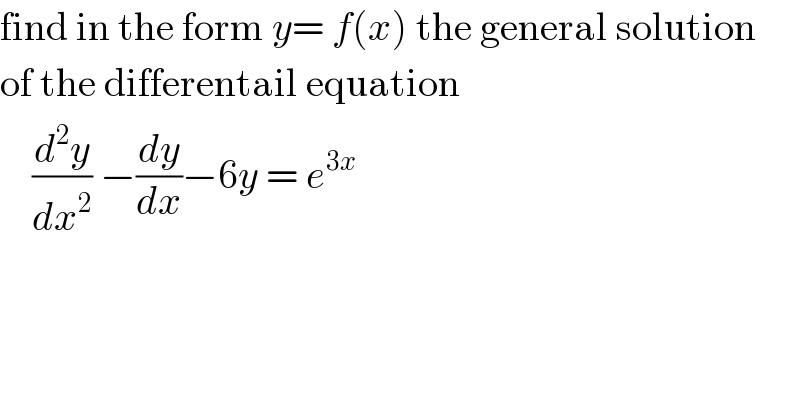
$$\mathrm{find}\:\mathrm{in}\:\mathrm{the}\:\mathrm{form}\:{y}=\:{f}\left({x}\right)\:\mathrm{the}\:\mathrm{general}\:\mathrm{solution}\: \\ $$$$\mathrm{of}\:\mathrm{the}\:\mathrm{differentail}\:\mathrm{equation} \\ $$$$\:\:\:\:\frac{{d}^{\mathrm{2}} {y}}{{dx}^{\mathrm{2}} }\:−\frac{{dy}}{{dx}}−\mathrm{6}{y}\:=\:{e}^{\mathrm{3}{x}} \\ $$$$ \\ $$
Commented by niroj last updated on 06/Apr/20

$$\:\:\frac{\mathrm{d}^{\mathrm{2}} \mathrm{y}}{\mathrm{dx}^{\mathrm{2}} }−\frac{\mathrm{dy}}{\mathrm{dx}}−\mathrm{6y}=\mathrm{e}^{\mathrm{3x}} \\ $$$$\:\:\mathrm{let},\:\frac{\mathrm{d}^{\mathrm{2}} \mathrm{y}}{\mathrm{dx}^{\mathrm{2}} }=\mathrm{D}^{\mathrm{2}} \mathrm{y}\:\mathrm{and}\:\frac{\mathrm{dy}}{\mathrm{dx}}=\mathrm{Dy} \\ $$$$\:\:\:\left(\mathrm{D}^{\mathrm{2}} −\mathrm{D}−\mathrm{6}\right)\mathrm{y}=\mathrm{e}^{\mathrm{3x}} \\ $$$$\:\:\mathrm{Auxilairy}\:\mathrm{Equation}, \\ $$$$\:\:\:\:\:\mathrm{m}^{\mathrm{2}} −\mathrm{m}−\mathrm{6}=\mathrm{0} \\ $$$$\:\:\:\:\:\mathrm{m}^{\mathrm{2}} −\mathrm{3m}+\mathrm{2m}−\mathrm{6}=\mathrm{0} \\ $$$$\:\:\:\mathrm{m}\left(\mathrm{m}−\mathrm{3}\right)+\mathrm{2}\left(\mathrm{m}−\mathrm{3}\right)=\mathrm{0} \\ $$$$\:\:\:\:\:\:\:\:\:\left(\mathrm{m}−\mathrm{3}\right)\left(\mathrm{m}+\mathrm{2}\right)=\mathrm{0} \\ $$$$\:\:\:\:\:\mathrm{m}=\:\mathrm{3},−\mathrm{2} \\ $$$$\:\:\mathrm{Complementary}\:\mathrm{Fuction}\:=\:\mathrm{C}_{\mathrm{1}} \mathrm{e}^{\mathrm{3x}} +\mathrm{C}_{\mathrm{2}} \mathrm{e}^{−\mathrm{2x}} \\ $$$$\:\:\mathrm{Particular}\:\mathrm{Integral}=\:\frac{\mathrm{e}^{\mathrm{3x}} }{\mathrm{D}^{\mathrm{2}} −\mathrm{D}−\mathrm{6}} \\ $$$$\:\:\:\:\:\:=\:\frac{\mathrm{x}.\mathrm{e}^{\mathrm{3x}} }{\mathrm{2D}−\mathrm{1}}=\:\frac{\mathrm{xe}^{\mathrm{3x}} }{\mathrm{6}−\mathrm{1}}=\:\frac{\mathrm{xe}^{\mathrm{3x}} }{\mathrm{5}} \\ $$$$\:\:\:\:\mathrm{y}=\:\mathrm{f}\left(\mathrm{x}\right)=\mathrm{CF}+\mathrm{PI} \\ $$$$\:\:\:\:\mathrm{y}=\:\mathrm{C}_{\mathrm{1}} \mathrm{e}^{\mathrm{3x}} +\mathrm{C}_{\mathrm{2}} \mathrm{e}^{−\mathrm{2x}} +\:\frac{\mathrm{xe}^{\mathrm{3x}} }{\mathrm{5}}//. \\ $$
Commented by Rio Michael last updated on 06/Apr/20

$$\mathrm{thanks}\:\mathrm{sir} \\ $$
