
Question Number 87733 by TawaTawa1 last updated on 05/Apr/20

Commented by mahdi last updated on 05/Apr/20
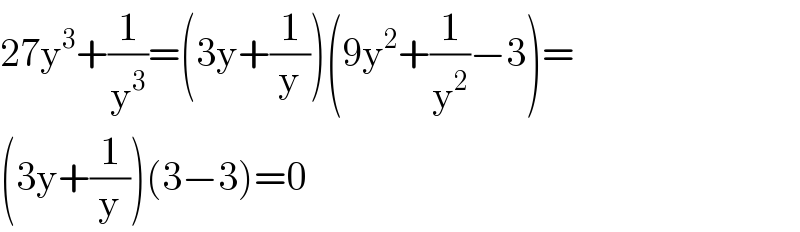
$$\mathrm{27y}^{\mathrm{3}} +\frac{\mathrm{1}}{\mathrm{y}^{\mathrm{3}} }=\left(\mathrm{3y}+\frac{\mathrm{1}}{\mathrm{y}}\right)\left(\mathrm{9y}^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{y}^{\mathrm{2}} }−\mathrm{3}\right)= \\ $$$$\left(\mathrm{3y}+\frac{\mathrm{1}}{\mathrm{y}}\right)\left(\mathrm{3}−\mathrm{3}\right)=\mathrm{0} \\ $$
Commented by TawaTawa1 last updated on 05/Apr/20
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$
Answered by mind is power last updated on 05/Apr/20
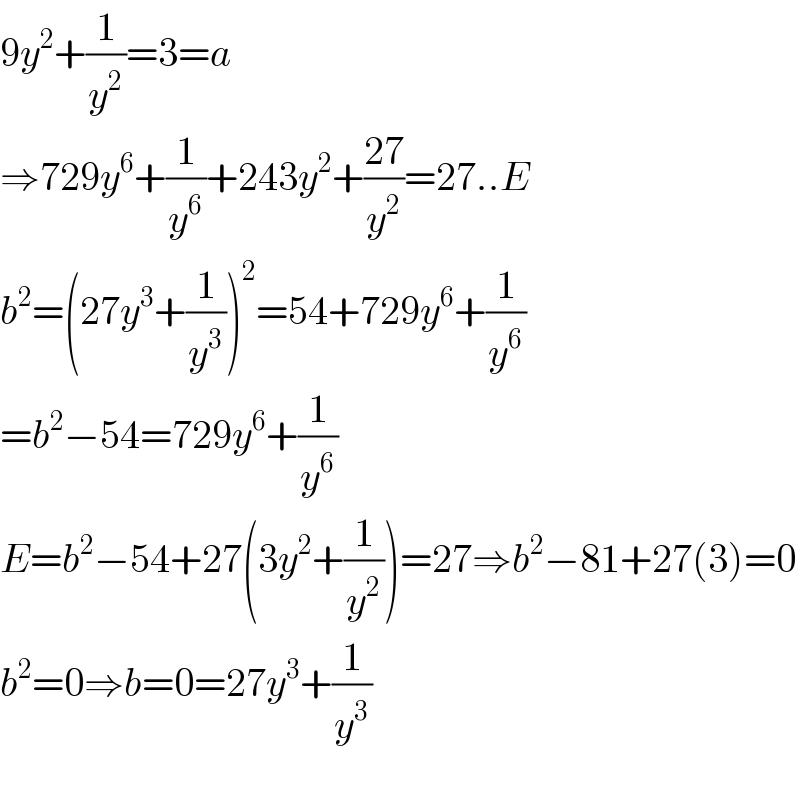
$$\mathrm{9}{y}^{\mathrm{2}} +\frac{\mathrm{1}}{{y}^{\mathrm{2}} }=\mathrm{3}={a} \\ $$$$\Rightarrow\mathrm{729}{y}^{\mathrm{6}} +\frac{\mathrm{1}}{{y}^{\mathrm{6}} }+\mathrm{243}{y}^{\mathrm{2}} +\frac{\mathrm{27}}{{y}^{\mathrm{2}} }=\mathrm{27}..{E} \\ $$$${b}^{\mathrm{2}} =\left(\mathrm{27}{y}^{\mathrm{3}} +\frac{\mathrm{1}}{{y}^{\mathrm{3}} }\right)^{\mathrm{2}} =\mathrm{54}+\mathrm{729}{y}^{\mathrm{6}} +\frac{\mathrm{1}}{{y}^{\mathrm{6}} } \\ $$$$={b}^{\mathrm{2}} −\mathrm{54}=\mathrm{729}{y}^{\mathrm{6}} +\frac{\mathrm{1}}{{y}^{\mathrm{6}} } \\ $$$${E}={b}^{\mathrm{2}} −\mathrm{54}+\mathrm{27}\left(\mathrm{3}{y}^{\mathrm{2}} +\frac{\mathrm{1}}{{y}^{\mathrm{2}} }\right)=\mathrm{27}\Rightarrow{b}^{\mathrm{2}} −\mathrm{81}+\mathrm{27}\left(\mathrm{3}\right)=\mathrm{0} \\ $$$${b}^{\mathrm{2}} =\mathrm{0}\Rightarrow{b}=\mathrm{0}=\mathrm{27}{y}^{\mathrm{3}} +\frac{\mathrm{1}}{{y}^{\mathrm{3}} } \\ $$$$ \\ $$
Commented by TawaTawa1 last updated on 05/Apr/20
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$
Commented by mind is power last updated on 05/Apr/20

$${you}\:{too}\:{miss} \\ $$
