
Question Number 867 by sagarwal last updated on 03/Apr/15
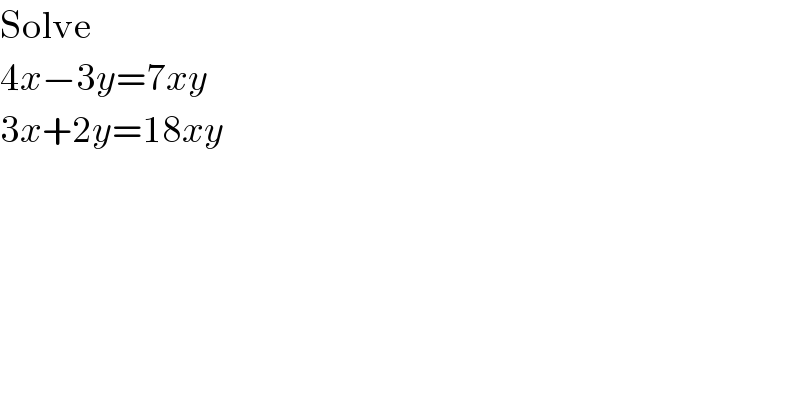
$$\mathrm{Solve} \\ $$$$\mathrm{4}{x}−\mathrm{3}{y}=\mathrm{7}{xy} \\ $$$$\mathrm{3}{x}+\mathrm{2}{y}=\mathrm{18}{xy} \\ $$
Commented by 123456 last updated on 03/Apr/15
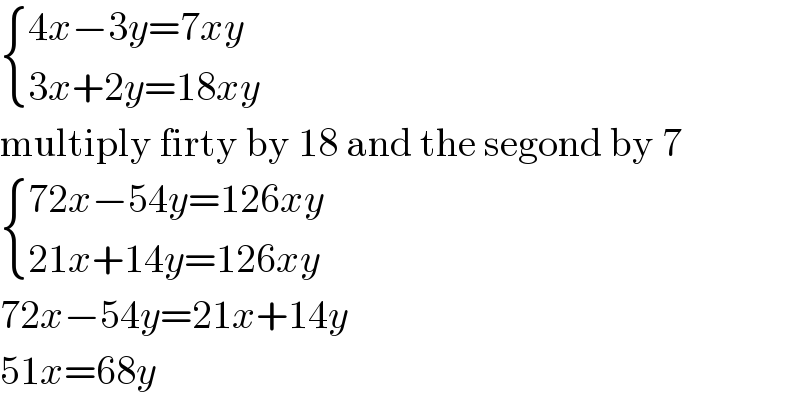
$$\begin{cases}{\mathrm{4}{x}−\mathrm{3}{y}=\mathrm{7}{xy}}\\{\mathrm{3}{x}+\mathrm{2}{y}=\mathrm{18}{xy}}\end{cases} \\ $$$$\mathrm{multiply}\:\mathrm{firty}\:\mathrm{by}\:\mathrm{18}\:\mathrm{and}\:\mathrm{the}\:\mathrm{segond}\:\mathrm{by}\:\mathrm{7} \\ $$$$\begin{cases}{\mathrm{72}{x}−\mathrm{54}{y}=\mathrm{126}{xy}}\\{\mathrm{21}{x}+\mathrm{14}{y}=\mathrm{126}{xy}}\end{cases} \\ $$$$\mathrm{72}{x}−\mathrm{54}{y}=\mathrm{21}{x}+\mathrm{14}{y} \\ $$$$\mathrm{51}{x}=\mathrm{68}{y} \\ $$
Answered by 123456 last updated on 03/Apr/15
![by coments y=((3x)/4) substituting in first equation 4x−((9x)/4)=((21x^2 )/4) 21x^2 =7x 21x^2 −7x=0 7x(3x−1)=0 x=0∨x=(1/3) [(x),(y) ]= [(0),(0) ]∨ [(x),(y) ]= [((1/3)),((1/4)) ]](Q869.png)
$$\mathrm{by}\:\mathrm{coments} \\ $$$${y}=\frac{\mathrm{3}{x}}{\mathrm{4}} \\ $$$$\mathrm{substituting}\:\mathrm{in}\:\mathrm{first}\:\mathrm{equation} \\ $$$$\mathrm{4}{x}−\frac{\mathrm{9}{x}}{\mathrm{4}}=\frac{\mathrm{21}{x}^{\mathrm{2}} }{\mathrm{4}} \\ $$$$\mathrm{21}{x}^{\mathrm{2}} =\mathrm{7}{x} \\ $$$$\mathrm{21}{x}^{\mathrm{2}} −\mathrm{7}{x}=\mathrm{0} \\ $$$$\mathrm{7}{x}\left(\mathrm{3}{x}−\mathrm{1}\right)=\mathrm{0} \\ $$$${x}=\mathrm{0}\vee{x}=\frac{\mathrm{1}}{\mathrm{3}} \\ $$$$\begin{bmatrix}{{x}}\\{{y}}\end{bmatrix}=\begin{bmatrix}{\mathrm{0}}\\{\mathrm{0}}\end{bmatrix}\vee\begin{bmatrix}{{x}}\\{{y}}\end{bmatrix}=\begin{bmatrix}{\frac{\mathrm{1}}{\mathrm{3}}}\\{\frac{\mathrm{1}}{\mathrm{4}}}\end{bmatrix} \\ $$
