Question and Answers Forum

All Questions      Topic List

Differential Equation Questions

Previous in All Question      Next in All Question      

Previous in Differential Equation      Next in Differential Equation      

Question Number 86142 by jagoll last updated on 27/Mar/20

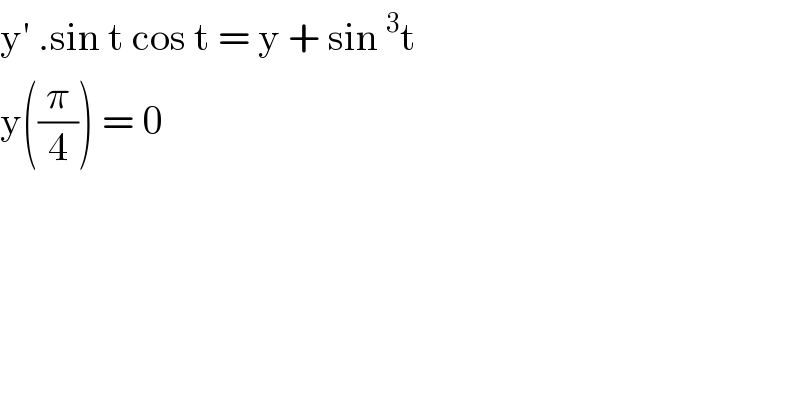
y′ .sin t cos t = y + sin^3 t y((π/4)) = 0

$$\mathrm{y}'\:.\mathrm{sin}\:\mathrm{t}\:\mathrm{cos}\:\mathrm{t}\:=\:\mathrm{y}\:+\:\mathrm{sin}\:^{\mathrm{3}} \mathrm{t}\: \\ $$$$\mathrm{y}\left(\frac{\pi}{\mathrm{4}}\right)\:=\:\mathrm{0}\: \\ $$

Answered by Kunal12588 last updated on 27/Mar/20

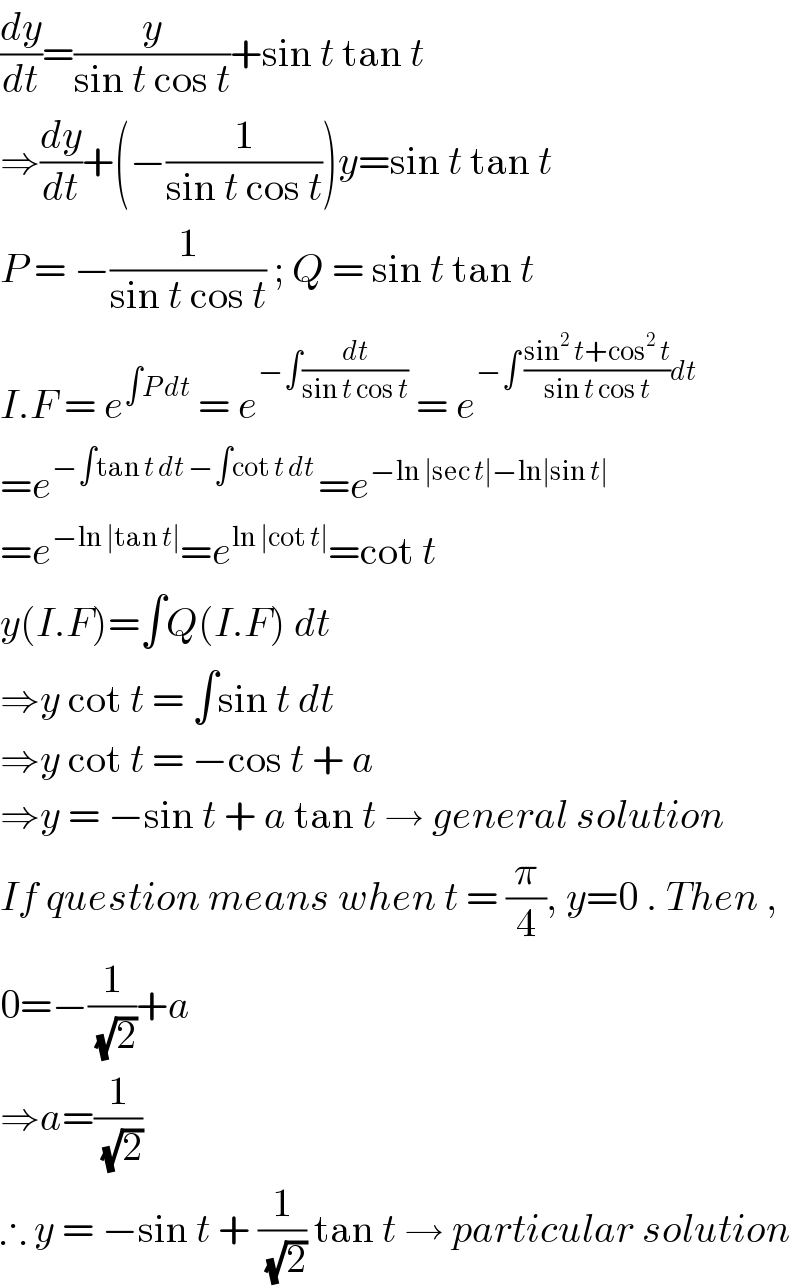
(dy/dt)=(y/(sin t cos t))+sin t tan t ⇒(dy/dt)+(−(1/(sin t cos t)))y=sin t tan t P = −(1/(sin t cos t)) ; Q = sin t tan t I.F = e^(∫P dt) = e^(−∫(dt/(sin t cos t))) = e^(−∫ ((sin^2 t+cos^2 t)/(sin t cos t))dt) =e^(−∫tan t dt −∫cot t dt ) =e^(−ln ∣sec t∣−ln∣sin t∣ ) =e^(−ln ∣tan t∣) =e^(ln ∣cot t∣) =cot t y(I.F)=∫Q(I.F) dt ⇒y cot t = ∫sin t dt ⇒y cot t = −cos t + a ⇒y = −sin t + a tan t → general solution If question means when t = (π/4), y=0 . Then , 0=−(1/(√2))+a ⇒a=(1/(√2)) ∴ y = −sin t + (1/(√2)) tan t → particular solution

$$\frac{{dy}}{{dt}}=\frac{{y}}{\mathrm{sin}\:{t}\:\mathrm{cos}\:{t}}+\mathrm{sin}\:{t}\:\mathrm{tan}\:{t} \\ $$$$\Rightarrow\frac{{dy}}{{dt}}+\left(−\frac{\mathrm{1}}{\mathrm{sin}\:{t}\:\mathrm{cos}\:{t}}\right){y}=\mathrm{sin}\:{t}\:\mathrm{tan}\:{t} \\ $$$${P}\:=\:−\frac{\mathrm{1}}{\mathrm{sin}\:{t}\:\mathrm{cos}\:{t}}\:;\:{Q}\:=\:\mathrm{sin}\:{t}\:\mathrm{tan}\:{t} \\ $$$${I}.{F}\:=\:{e}^{\int{P}\:{dt}} \:=\:{e}^{−\int\frac{{dt}}{\mathrm{sin}\:{t}\:\mathrm{cos}\:{t}}} \:=\:{e}^{−\int\:\frac{\mathrm{sin}^{\mathrm{2}} \:{t}+\mathrm{cos}^{\mathrm{2}} \:{t}}{\mathrm{sin}\:{t}\:\mathrm{cos}\:{t}}{dt}} \\ $$$$={e}^{−\int\mathrm{tan}\:{t}\:{dt}\:−\int\mathrm{cot}\:{t}\:{dt}\:} ={e}^{−\mathrm{ln}\:\mid\mathrm{sec}\:{t}\mid−\mathrm{ln}\mid\mathrm{sin}\:{t}\mid\:} \\ $$$$={e}^{−\mathrm{ln}\:\mid\mathrm{tan}\:{t}\mid} ={e}^{\mathrm{ln}\:\mid\mathrm{cot}\:{t}\mid} =\mathrm{cot}\:{t} \\ $$$${y}\left({I}.{F}\right)=\int{Q}\left({I}.{F}\right)\:{dt} \\ $$$$\Rightarrow{y}\:\mathrm{cot}\:{t}\:=\:\int\mathrm{sin}\:{t}\:{dt} \\ $$$$\Rightarrow{y}\:\mathrm{cot}\:{t}\:=\:−\mathrm{cos}\:{t}\:+\:{a} \\ $$$$\Rightarrow{y}\:=\:−\mathrm{sin}\:{t}\:+\:{a}\:\mathrm{tan}\:{t}\:\rightarrow\:{general}\:{solution} \\ $$$${If}\:{question}\:{means}\:{when}\:{t}\:=\:\frac{\pi}{\mathrm{4}},\:{y}=\mathrm{0}\:.\:{Then}\:, \\ $$$$\mathrm{0}=−\frac{\mathrm{1}}{\sqrt{\mathrm{2}}}+{a} \\ $$$$\Rightarrow{a}=\frac{\mathrm{1}}{\sqrt{\mathrm{2}}} \\ $$$$\therefore\:{y}\:=\:−\mathrm{sin}\:{t}\:+\:\frac{\mathrm{1}}{\sqrt{\mathrm{2}}}\:\mathrm{tan}\:{t}\:\rightarrow\:{particular}\:{solution} \\ $$

Commented by jagoll last updated on 27/Mar/20

thank you sir

$$\mathrm{thank}\:\mathrm{you}\:\mathrm{sir} \\ $$

Answered by TANMAY PANACEA. last updated on 27/Mar/20

(dy/dt)+((−y)/(sintcost))=((sin^2 t)/(cost)) e^(∫(dt/(−sintcost))) e^(∫−2cosec2t dt) ∫cosec2t=((lntant)/2) e^(∫−2cosec2t ) dt=e^(−2×((lntant)/2)) =(1/(tant))=cott cott×(dy/dt)+((−y×cott)/(sint×cost))=((sin^2 t)/(cost))×cott cott×(dy/dt)+y×(−cosec^2 t)=sint (d/dt)(y.cott)=sint ycott=−cost+c 0×1=−(1/(√2))+c ycott=−cost+(1/(√2))

$$\frac{{dy}}{{dt}}+\frac{−{y}}{{sintcost}}=\frac{{sin}^{\mathrm{2}} {t}}{{cost}} \\ $$$${e}^{\int\frac{{dt}}{−{sintcost}}} \\ $$$${e}^{\int−\mathrm{2}{cosec}\mathrm{2}{t}\:{dt}} \\ $$$$\int{cosec}\mathrm{2}{t}=\frac{{lntant}}{\mathrm{2}} \\ $$$${e}^{\int−\mathrm{2}{cosec}\mathrm{2}{t}\:} {dt}={e}^{−\mathrm{2}×\frac{{lntant}}{\mathrm{2}}} =\frac{\mathrm{1}}{{tant}}={cott} \\ $$$${cott}×\frac{{dy}}{{dt}}+\frac{−{y}×{cott}}{{sint}×{cost}}=\frac{{sin}^{\mathrm{2}} {t}}{{cost}}×{cott} \\ $$$${cott}×\frac{{dy}}{{dt}}+{y}×\left(−{cosec}^{\mathrm{2}} {t}\right)={sint} \\ $$$$\frac{{d}}{{dt}}\left({y}.{cott}\right)={sint} \\ $$$${ycott}=−{cost}+{c} \\ $$$$\mathrm{0}×\mathrm{1}=−\frac{\mathrm{1}}{\sqrt{\mathrm{2}}}+{c} \\ $$$${ycott}=−{cost}+\frac{\mathrm{1}}{\sqrt{\mathrm{2}}} \\ $$

Commented by jagoll last updated on 27/Mar/20

what is cott sir?

$$\mathrm{what}\:\mathrm{is}\:\mathrm{cott}\:\mathrm{sir}? \\ $$

Commented by TANMAY PANACEA. last updated on 27/Mar/20

cotθ → cot(t)

$${cot}\theta\:\rightarrow\:\:\:{cot}\left({t}\right) \\ $$

Commented by jagoll last updated on 27/Mar/20

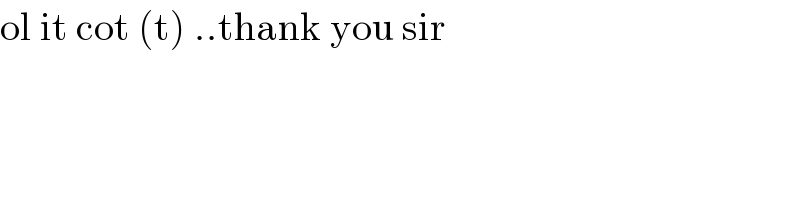
ol it cot (t) ..thank you sir

$$\mathrm{ol}\:\mathrm{it}\:\mathrm{cot}\:\left(\mathrm{t}\right)\:..\mathrm{thank}\:\mathrm{you}\:\mathrm{sir} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com