
Previous in Differential Equation Next in Differential Equation
Question Number 86120 by jagoll last updated on 27/Mar/20
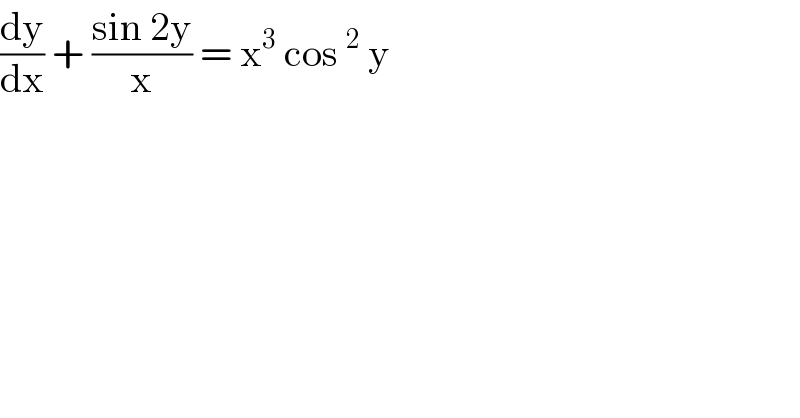
$$\frac{\mathrm{dy}}{\mathrm{dx}}\:+\:\frac{\mathrm{sin}\:\mathrm{2y}}{\mathrm{x}}\:=\:\mathrm{x}^{\mathrm{3}} \:\mathrm{cos}\:^{\mathrm{2}} \:\mathrm{y} \\ $$
Commented by Prithwish Sen 1 last updated on 27/Mar/20
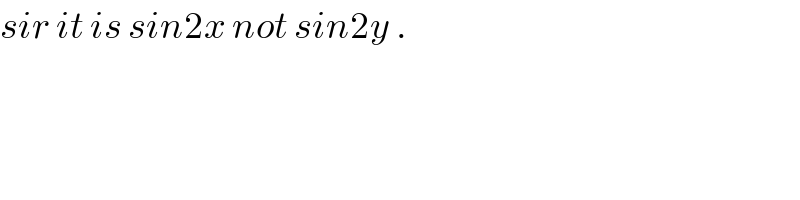
$${sir}\:{it}\:{is}\:{sin}\mathrm{2}{x}\:{not}\:{sin}\mathrm{2}{y}\:. \\ $$
Commented by jagoll last updated on 27/Mar/20

$$\mathrm{o}\:\mathrm{sorry}\:.\:\mathrm{i}'\mathrm{m}\:\mathrm{wrong}\:\mathrm{write}\:\mathrm{the}\: \\ $$$$\mathrm{equation}.\:\mathrm{i}\:\mathrm{will}\:\mathrm{correct} \\ $$
Commented by jagoll last updated on 27/Mar/20
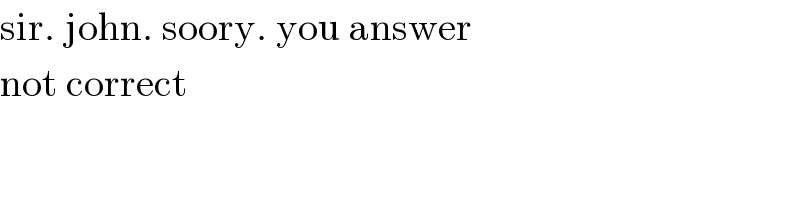
$$\mathrm{sir}.\:\mathrm{john}.\:\mathrm{soory}.\:\mathrm{you}\:\mathrm{answer}\: \\ $$$$\mathrm{not}\:\mathrm{correct} \\ $$
Commented by john santu last updated on 27/Mar/20

$${ok} \\ $$
Commented by niroj last updated on 27/Mar/20
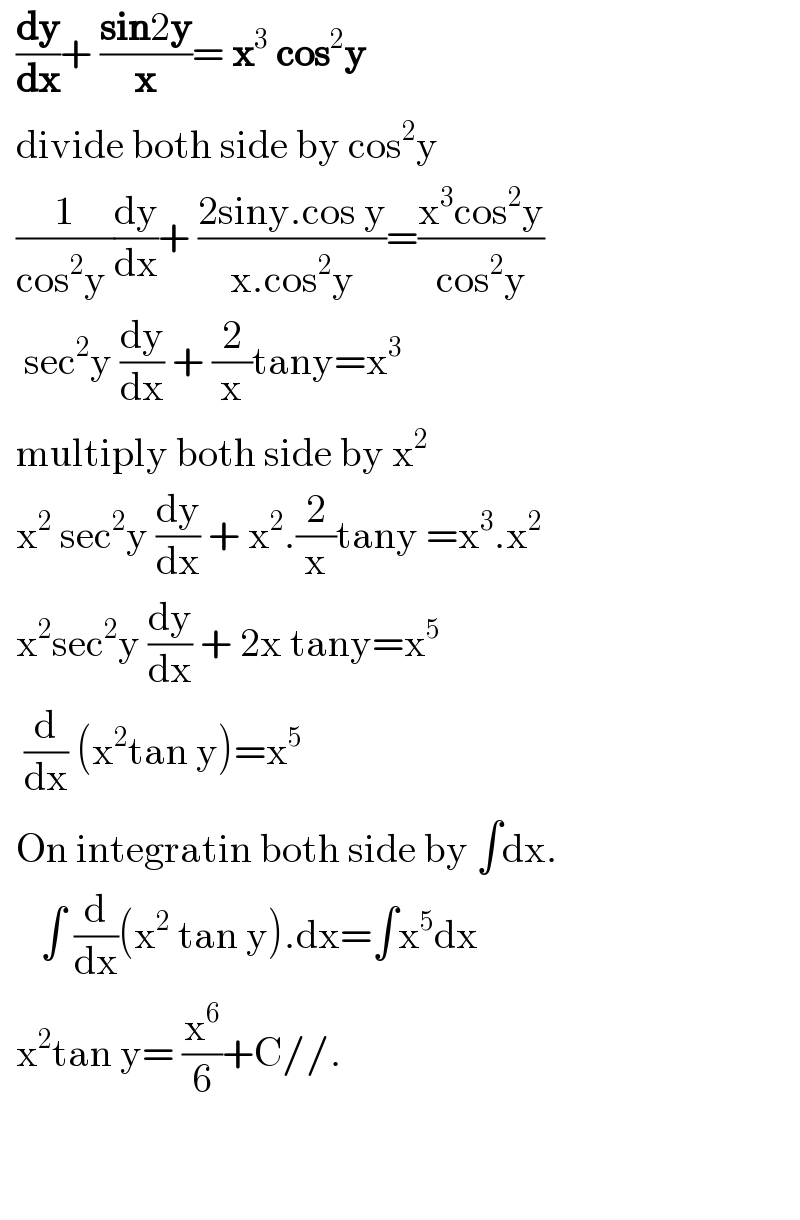
$$\:\:\frac{\boldsymbol{\mathrm{dy}}}{\boldsymbol{\mathrm{dx}}}+\:\frac{\boldsymbol{\mathrm{sin}}\mathrm{2}\boldsymbol{\mathrm{y}}}{\boldsymbol{\mathrm{x}}}=\:\boldsymbol{\mathrm{x}}^{\mathrm{3}} \:\boldsymbol{\mathrm{cos}}^{\mathrm{2}} \boldsymbol{\mathrm{y}} \\ $$$$\:\:\mathrm{divide}\:\mathrm{both}\:\mathrm{side}\:\mathrm{by}\:\mathrm{cos}^{\mathrm{2}} \mathrm{y}\:\:\: \\ $$$$\:\:\frac{\mathrm{1}}{\mathrm{cos}^{\mathrm{2}} \mathrm{y}\:}\frac{\mathrm{dy}}{\mathrm{dx}}+\:\frac{\mathrm{2siny}.\mathrm{cos}\:\mathrm{y}}{\mathrm{x}.\mathrm{cos}^{\mathrm{2}} \mathrm{y}}=\frac{\mathrm{x}^{\mathrm{3}} \mathrm{cos}^{\mathrm{2}} \mathrm{y}}{\mathrm{cos}^{\mathrm{2}} \mathrm{y}} \\ $$$$\:\:\:\mathrm{sec}^{\mathrm{2}} \mathrm{y}\:\frac{\mathrm{dy}}{\mathrm{dx}}\:+\:\frac{\mathrm{2}}{\mathrm{x}}\mathrm{tany}=\mathrm{x}^{\mathrm{3}} \\ $$$$\:\:\mathrm{multiply}\:\mathrm{both}\:\mathrm{side}\:\mathrm{by}\:\mathrm{x}^{\mathrm{2}} \\ $$$$\:\:\mathrm{x}^{\mathrm{2}} \:\mathrm{sec}^{\mathrm{2}} \mathrm{y}\:\frac{\mathrm{dy}}{\mathrm{dx}}\:+\:\mathrm{x}^{\mathrm{2}} .\frac{\mathrm{2}}{\mathrm{x}}\mathrm{tany}\:=\mathrm{x}^{\mathrm{3}} .\mathrm{x}^{\mathrm{2}} \\ $$$$\:\:\mathrm{x}^{\mathrm{2}} \mathrm{sec}^{\mathrm{2}} \mathrm{y}\:\frac{\mathrm{dy}}{\mathrm{dx}}\:+\:\mathrm{2x}\:\mathrm{tany}=\mathrm{x}^{\mathrm{5}} \\ $$$$\:\:\:\frac{\mathrm{d}}{\mathrm{dx}}\:\left(\mathrm{x}^{\mathrm{2}} \mathrm{tan}\:\mathrm{y}\right)=\mathrm{x}^{\mathrm{5}} \\ $$$$\:\:\mathrm{On}\:\mathrm{integratin}\:\mathrm{both}\:\mathrm{side}\:\mathrm{by}\:\int\mathrm{dx}. \\ $$$$\:\:\:\:\:\int\:\frac{\mathrm{d}}{\mathrm{dx}}\left(\mathrm{x}^{\mathrm{2}} \:\mathrm{tan}\:\mathrm{y}\right).\mathrm{dx}=\int\mathrm{x}^{\mathrm{5}} \mathrm{dx} \\ $$$$\:\:\mathrm{x}^{\mathrm{2}} \mathrm{tan}\:\mathrm{y}=\:\frac{\mathrm{x}^{\mathrm{6}} }{\mathrm{6}}+\mathrm{C}//. \\ $$$$\:\: \\ $$$$\:\: \\ $$
Answered by mind is power last updated on 27/Mar/20
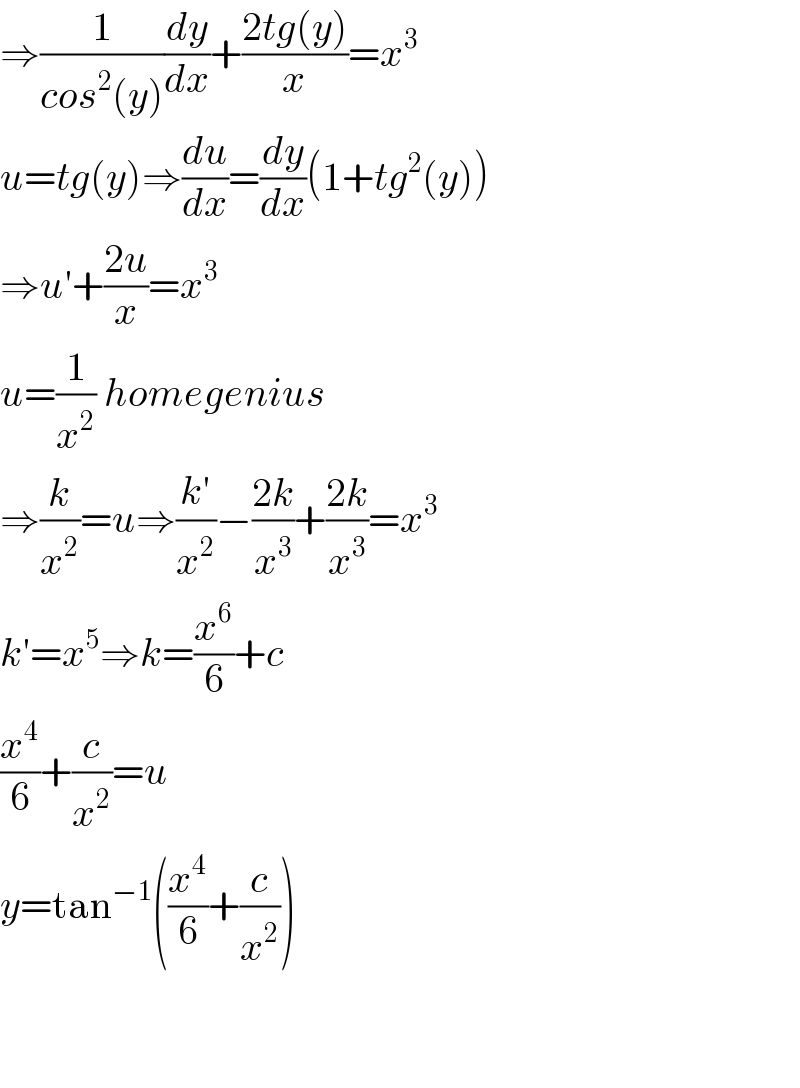
$$\Rightarrow\frac{\mathrm{1}}{{cos}^{\mathrm{2}} \left({y}\right)}\frac{{dy}}{{dx}}+\frac{\mathrm{2}{tg}\left({y}\right)}{{x}}={x}^{\mathrm{3}} \\ $$$${u}={tg}\left({y}\right)\Rightarrow\frac{{du}}{{dx}}=\frac{{dy}}{{dx}}\left(\mathrm{1}+{tg}^{\mathrm{2}} \left({y}\right)\right) \\ $$$$\Rightarrow{u}'+\frac{\mathrm{2}{u}}{{x}}={x}^{\mathrm{3}} \\ $$$${u}=\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\:{homegenius} \\ $$$$\Rightarrow\frac{{k}}{{x}^{\mathrm{2}} }={u}\Rightarrow\frac{{k}'}{{x}^{\mathrm{2}} }−\frac{\mathrm{2}{k}}{{x}^{\mathrm{3}} }+\frac{\mathrm{2}{k}}{{x}^{\mathrm{3}} }={x}^{\mathrm{3}} \\ $$$${k}'={x}^{\mathrm{5}} \Rightarrow{k}=\frac{{x}^{\mathrm{6}} }{\mathrm{6}}+{c} \\ $$$$\frac{{x}^{\mathrm{4}} }{\mathrm{6}}+\frac{{c}}{{x}^{\mathrm{2}} }={u} \\ $$$${y}=\mathrm{tan}^{−\mathrm{1}} \left(\frac{{x}^{\mathrm{4}} }{\mathrm{6}}+\frac{{c}}{{x}^{\mathrm{2}} }\right) \\ $$$$ \\ $$$$ \\ $$
