Question and Answers Forum

All Questions      Topic List

Mensuration Questions

Previous in All Question      Next in All Question      

Previous in Mensuration      Next in Mensuration      

Question Number 86113 by Tony Lin last updated on 27/Mar/20

(1)Determine the following if it is convergent or divergent Σ_(n=1) ^∞ ((sin(n))/n) (2)Σ_(n=1) ^∞ ((sin(n^p ))/n^p ), pεR,find the range of p when it is convergent

$$\left(\mathrm{1}\right){Determine}\:{the}\:{following} \\ $$$${if}\:{it}\:{is}\:{convergent}\:{or}\:{divergent} \\ $$$$\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{{sin}\left({n}\right)}{{n}} \\ $$$$\left(\mathrm{2}\right)\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{{sin}\left({n}^{{p}} \right)}{{n}^{{p}} },\:{p}\epsilon\mathbb{R},{find}\:{the}\:{range}\: \\ $$$${of}\:{p}\:{when}\:{it}\:{is}\:{convergent} \\ $$

Commented by Serlea last updated on 27/Mar/20

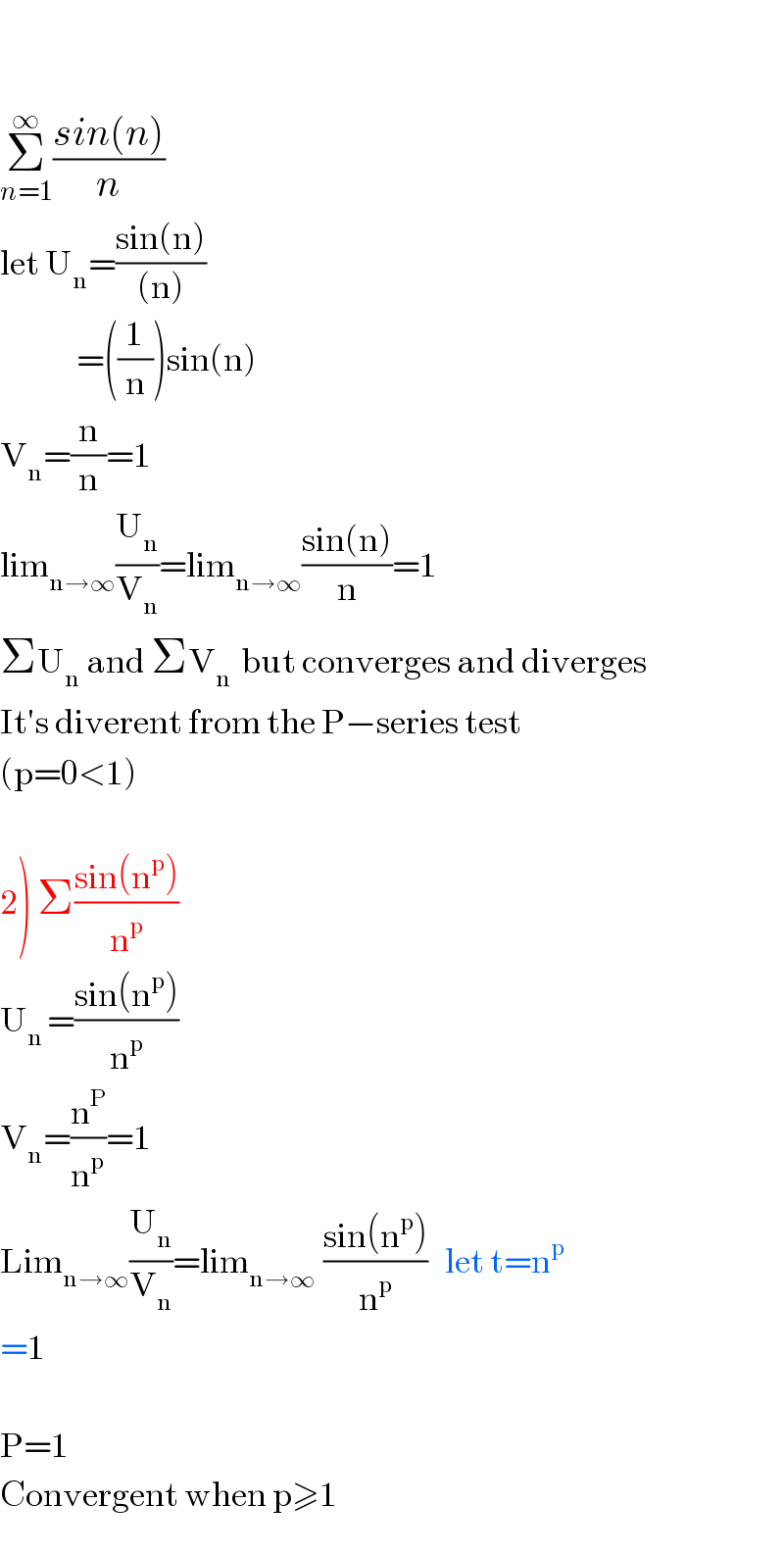
Σ_(n=1) ^∞ ((sin(n))/n) let U_n =((sin(n))/((n))) =((1/n))sin(n) V_n =(n/n)=1 lim_(n→∞) (U_n /V_n )=lim_(n→∞) ((sin(n))/n)=1 ΣU_n and ΣV_(n ) but converges and diverges It′s diverent from the P−series test (p=0<1) 2) Σ((sin(n^p ))/n^p ) U_(n ) =((sin(n^p ))/n^p ) V_n =(n^P /n^p )=1 Lim_(n→∞) (U_n /V_n )=lim_(n→∞ ) ((sin(n^p ))/n^p ) let t=n^p =1 P=1 Convergent when p≥1

$$ \\ $$$$ \\ $$$$\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{{sin}\left({n}\right)}{{n}} \\ $$$$\mathrm{let}\:\mathrm{U}_{\mathrm{n}} =\frac{\mathrm{sin}\left(\mathrm{n}\right)}{\left(\mathrm{n}\right)} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:=\left(\frac{\mathrm{1}}{\mathrm{n}}\right)\mathrm{sin}\left(\mathrm{n}\right) \\ $$$$\mathrm{V}_{\mathrm{n}} =\frac{\mathrm{n}}{\mathrm{n}}=\mathrm{1} \\ $$$$\mathrm{lim}_{\mathrm{n}\rightarrow\infty} \frac{\mathrm{U}_{\mathrm{n}} }{\mathrm{V}_{\mathrm{n}} }=\mathrm{lim}_{\mathrm{n}\rightarrow\infty} \frac{\mathrm{sin}\left(\mathrm{n}\right)}{\mathrm{n}}=\mathrm{1} \\ $$$$\Sigma\mathrm{U}_{\mathrm{n}} \:\mathrm{and}\:\Sigma\mathrm{V}_{\mathrm{n}\:} \:\mathrm{but}\:\mathrm{converges}\:\mathrm{and}\:\mathrm{diverges} \\ $$$$\mathrm{It}'\mathrm{s}\:\mathrm{diverent}\:\mathrm{from}\:\mathrm{the}\:\mathrm{P}−\mathrm{series}\:\mathrm{test} \\ $$$$\left(\mathrm{p}=\mathrm{0}<\mathrm{1}\right) \\ $$$$ \\ $$$$\left.\mathrm{2}\right)\:\Sigma\frac{\mathrm{sin}\left(\mathrm{n}^{\mathrm{p}} \right)}{\mathrm{n}^{\mathrm{p}} } \\ $$$$\mathrm{U}_{\mathrm{n}\:} =\frac{\mathrm{sin}\left(\mathrm{n}^{\mathrm{p}} \right)}{\mathrm{n}^{\mathrm{p}} } \\ $$$$\mathrm{V}_{\mathrm{n}} =\frac{\mathrm{n}^{\mathrm{P}} }{\mathrm{n}^{\mathrm{p}} }=\mathrm{1} \\ $$$$\mathrm{Lim}_{\mathrm{n}\rightarrow\infty} \frac{\mathrm{U}_{\mathrm{n}} }{\mathrm{V}_{\mathrm{n}} }=\mathrm{lim}_{\mathrm{n}\rightarrow\infty\:\:} \frac{\mathrm{sin}\left(\mathrm{n}^{\mathrm{p}} \right)}{\mathrm{n}^{\mathrm{p}} }\:\:\:\mathrm{let}\:\mathrm{t}=\mathrm{n}^{\mathrm{p}} \\ $$$$=\mathrm{1} \\ $$$$ \\ $$$$\mathrm{P}=\mathrm{1} \\ $$$$\mathrm{Convergent}\:\mathrm{when}\:\mathrm{p}\geqslant\mathrm{1} \\ $$

Commented by mathmax by abdo last updated on 27/Mar/20

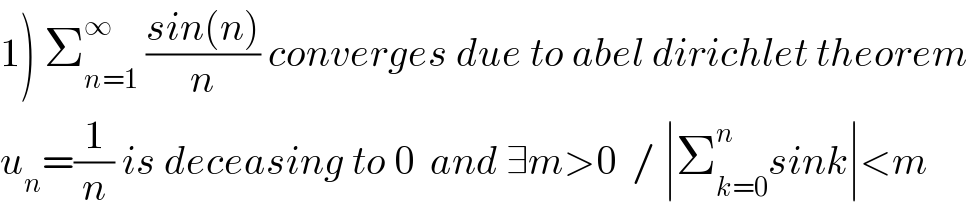
1) Σ_(n=1) ^∞ ((sin(n))/n) converges due to abel dirichlet theorem u_n =(1/n) is deceasing to 0 and ∃m>0 / ∣Σ_(k=0) ^(n ) sink∣<m

$$\left.\mathrm{1}\right)\:\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{{sin}\left({n}\right)}{{n}}\:{converges}\:{due}\:{to}\:{abel}\:{dirichlet}\:{theorem} \\ $$$${u}_{{n}} =\frac{\mathrm{1}}{{n}}\:{is}\:{deceasing}\:{to}\:\mathrm{0}\:\:{and}\:\exists{m}>\mathrm{0}\:\:/\:\mid\sum_{{k}=\mathrm{0}} ^{{n}\:} {sink}\mid<{m} \\ $$

Commented by mathmax by abdo last updated on 27/Mar/20

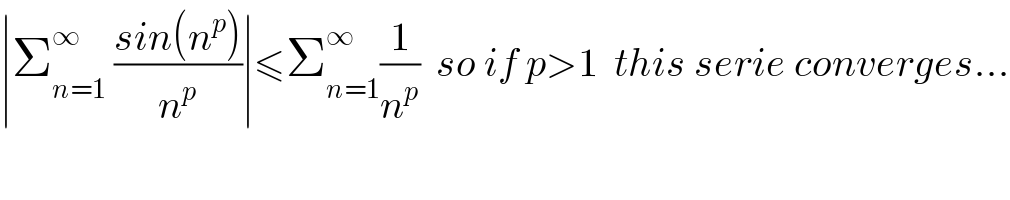
∣Σ_(n=1) ^∞ ((sin(n^p ))/n^p )∣≤Σ_(n=1) ^∞ (1/n^p ) so if p>1 this serie converges...

$$\mid\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{{sin}\left({n}^{{p}} \right)}{{n}^{{p}} }\mid\leqslant\sum_{{n}=\mathrm{1}} ^{\infty} \frac{\mathrm{1}}{{n}^{{p}} }\:\:{so}\:{if}\:{p}>\mathrm{1}\:\:{this}\:{serie}\:{converges}... \\ $$

Commented by Serlea last updated on 27/Mar/20

I think you are wrong bro

$$\mathrm{I}\:\mathrm{think}\:\mathrm{you}\:\mathrm{are}\:\mathrm{wrong}\:\mathrm{bro} \\ $$

Commented by mathmax by abdo last updated on 27/Mar/20

i am not wrong revise courses of series....

$${i}\:{am}\:{not}\:{wrong}\:\:{revise}\:{courses}\:{of}\:{series}.... \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com