
Question Number 86111 by john santu last updated on 27/Mar/20
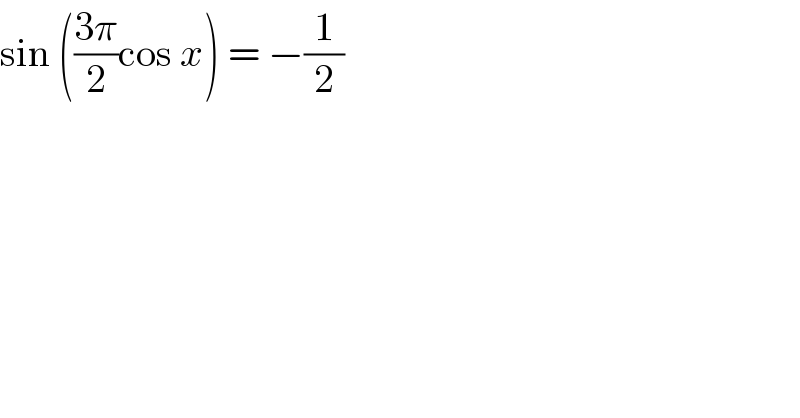
$$\mathrm{sin}\:\left(\frac{\mathrm{3}\pi}{\mathrm{2}}\mathrm{cos}\:{x}\right)\:=\:−\frac{\mathrm{1}}{\mathrm{2}} \\ $$
Commented by jagoll last updated on 27/Mar/20
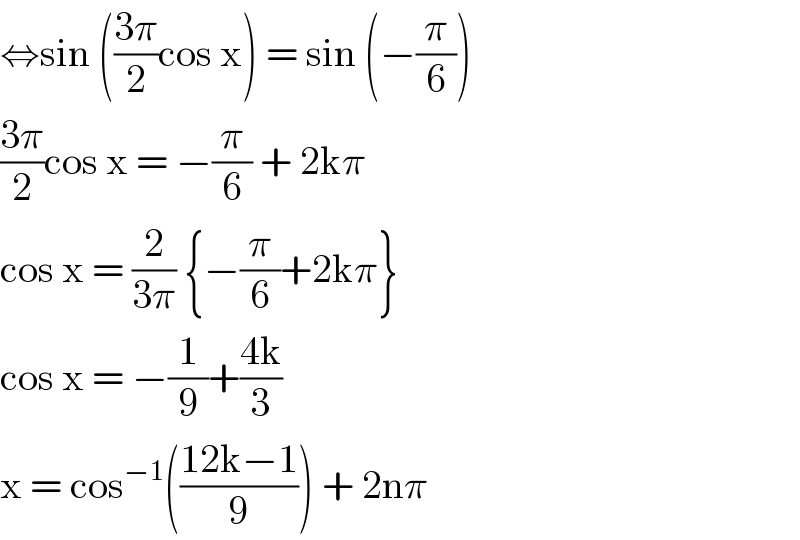
$$\Leftrightarrow\mathrm{sin}\:\left(\frac{\mathrm{3}\pi}{\mathrm{2}}\mathrm{cos}\:\mathrm{x}\right)\:=\:\mathrm{sin}\:\left(−\frac{\pi}{\mathrm{6}}\right) \\ $$$$\frac{\mathrm{3}\pi}{\mathrm{2}}\mathrm{cos}\:\mathrm{x}\:=\:−\frac{\pi}{\mathrm{6}}\:+\:\mathrm{2k}\pi \\ $$$$\mathrm{cos}\:\mathrm{x}\:=\:\frac{\mathrm{2}}{\mathrm{3}\pi}\:\left\{−\frac{\pi}{\mathrm{6}}+\mathrm{2k}\pi\right\} \\ $$$$\mathrm{cos}\:\mathrm{x}\:=\:−\frac{\mathrm{1}}{\mathrm{9}}+\frac{\mathrm{4k}}{\mathrm{3}} \\ $$$$\mathrm{x}\:=\:\mathrm{cos}^{−\mathrm{1}} \left(\frac{\mathrm{12k}−\mathrm{1}}{\mathrm{9}}\right)\:+\:\mathrm{2n}\pi \\ $$
Answered by TANMAY PANACEA. last updated on 27/Mar/20
![sin(((3π)/2)cosx)=sin(π+(π/6)) ((3π)/2)cosx=((7π)/6) cosx=(7/6)×(2/3)=(7/9)=cosα x=2nπ±α [α=cos^(−1) ((7/9))] ★ sin(((3π)/2)cosx)=−(1/2)=sin(((−π)/6)) ((3π)/2)cosx=((−π)/6) cosx=((−1)/9)=cosβ x=2nπ±β [β=cos^(−1) (((−1)/9))]](Q86115.png)
$${sin}\left(\frac{\mathrm{3}\pi}{\mathrm{2}}{cosx}\right)={sin}\left(\pi+\frac{\pi}{\mathrm{6}}\right) \\ $$$$\frac{\mathrm{3}\pi}{\mathrm{2}}{cosx}=\frac{\mathrm{7}\pi}{\mathrm{6}} \\ $$$${cosx}=\frac{\mathrm{7}}{\mathrm{6}}×\frac{\mathrm{2}}{\mathrm{3}}=\frac{\mathrm{7}}{\mathrm{9}}={cos}\alpha \\ $$$${x}=\mathrm{2}{n}\pi\pm\alpha\:\:\:\:\:\left[\alpha={cos}^{−\mathrm{1}} \left(\frac{\mathrm{7}}{\mathrm{9}}\right)\right] \\ $$$$\bigstar\:\:{sin}\left(\frac{\mathrm{3}\pi}{\mathrm{2}}{cosx}\right)=−\frac{\mathrm{1}}{\mathrm{2}}={sin}\left(\frac{−\pi}{\mathrm{6}}\right) \\ $$$$\frac{\mathrm{3}\pi}{\mathrm{2}}{cosx}=\frac{−\pi}{\mathrm{6}}\:\:\:\:\:\:\:{cosx}=\frac{−\mathrm{1}}{\mathrm{9}}={cos}\beta \\ $$$${x}=\mathrm{2}{n}\pi\pm\beta\:\:\:\left[\beta={cos}^{−\mathrm{1}} \left(\frac{−\mathrm{1}}{\mathrm{9}}\right)\right] \\ $$$$ \\ $$
Answered by mr W last updated on 27/Mar/20
![sin (((3π)/2)cos x) = −(1/2) ⇒((3π)/2)cos x = nπ−(−1)^n (π/6) ⇒cos x =(2/3)[n−(−1)^n (1/6)] ⇒−1≤(2/3)[n−(−1)^n (1/6)]≤1 ⇒n=−1, 0, 1 ⇒cos x =(2/3)[n−(−1)^n (1/6)]=−(5/9), −(1/9), (7/9) ⇒x=(2k+1)π±cos^(−1) (5/9) ⇒x=(2k+1)π±cos^(−1) (1/9) ⇒x=2kπ±cos^(−1) (7/9)](Q86133.png)
$$\mathrm{sin}\:\left(\frac{\mathrm{3}\pi}{\mathrm{2}}\mathrm{cos}\:{x}\right)\:=\:−\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\Rightarrow\frac{\mathrm{3}\pi}{\mathrm{2}}\mathrm{cos}\:{x}\:=\:{n}\pi−\left(−\mathrm{1}\right)^{{n}} \frac{\pi}{\mathrm{6}} \\ $$$$\Rightarrow\mathrm{cos}\:{x}\:=\frac{\mathrm{2}}{\mathrm{3}}\left[{n}−\left(−\mathrm{1}\right)^{{n}} \frac{\mathrm{1}}{\mathrm{6}}\right] \\ $$$$\Rightarrow−\mathrm{1}\leqslant\frac{\mathrm{2}}{\mathrm{3}}\left[{n}−\left(−\mathrm{1}\right)^{{n}} \frac{\mathrm{1}}{\mathrm{6}}\right]\leqslant\mathrm{1} \\ $$$$\Rightarrow{n}=−\mathrm{1},\:\mathrm{0},\:\mathrm{1} \\ $$$$\Rightarrow\mathrm{cos}\:{x}\:=\frac{\mathrm{2}}{\mathrm{3}}\left[{n}−\left(−\mathrm{1}\right)^{{n}} \frac{\mathrm{1}}{\mathrm{6}}\right]=−\frac{\mathrm{5}}{\mathrm{9}},\:−\frac{\mathrm{1}}{\mathrm{9}},\:\:\frac{\mathrm{7}}{\mathrm{9}} \\ $$$$\Rightarrow{x}=\left(\mathrm{2}{k}+\mathrm{1}\right)\pi\pm\mathrm{cos}^{−\mathrm{1}} \frac{\mathrm{5}}{\mathrm{9}} \\ $$$$\Rightarrow{x}=\left(\mathrm{2}{k}+\mathrm{1}\right)\pi\pm\mathrm{cos}^{−\mathrm{1}} \frac{\mathrm{1}}{\mathrm{9}} \\ $$$$\Rightarrow{x}=\mathrm{2}{k}\pi\pm\mathrm{cos}^{−\mathrm{1}} \frac{\mathrm{7}}{\mathrm{9}} \\ $$
