
Question Number 86062 by ar247 last updated on 26/Mar/20
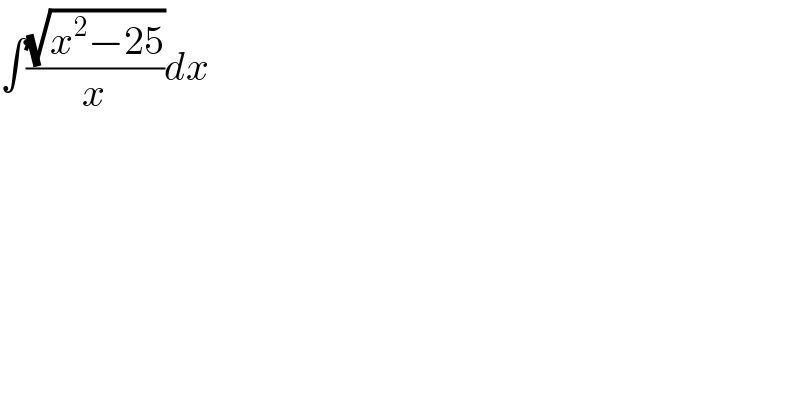
$$\int\frac{\sqrt{{x}^{\mathrm{2}} −\mathrm{25}}}{{x}}{dx} \\ $$
Commented by abdomathmax last updated on 27/Mar/20
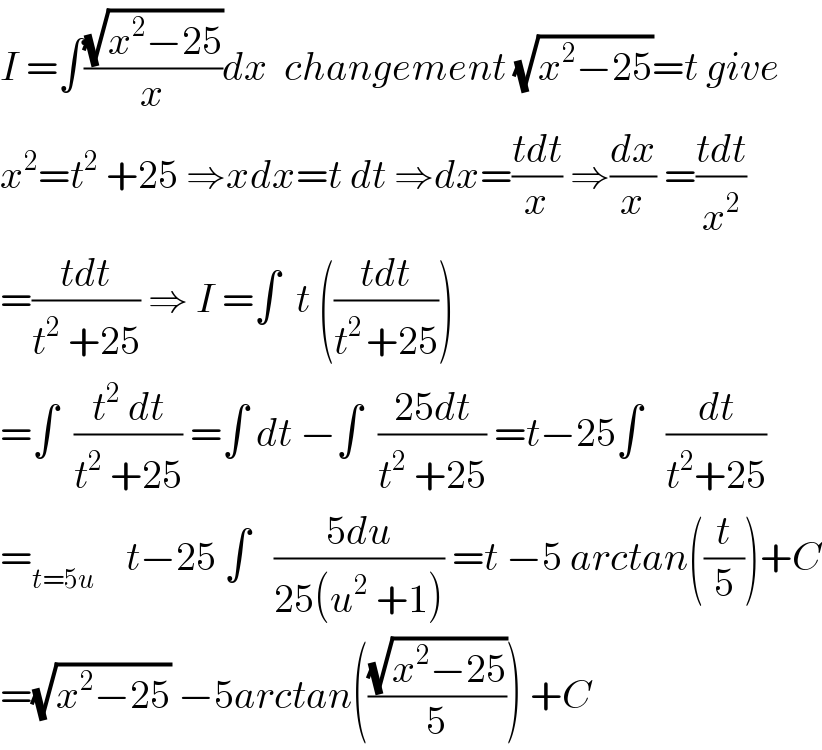
$${I}\:=\int\frac{\sqrt{{x}^{\mathrm{2}} −\mathrm{25}}}{{x}}{dx}\:\:{changement}\:\sqrt{{x}^{\mathrm{2}} −\mathrm{25}}={t}\:{give} \\ $$$${x}^{\mathrm{2}} ={t}^{\mathrm{2}} \:+\mathrm{25}\:\Rightarrow{xdx}={t}\:{dt}\:\Rightarrow{dx}=\frac{{tdt}}{{x}}\:\Rightarrow\frac{{dx}}{{x}}\:=\frac{{tdt}}{{x}^{\mathrm{2}} } \\ $$$$=\frac{{tdt}}{{t}^{\mathrm{2}} \:+\mathrm{25}}\:\Rightarrow\:{I}\:=\int\:\:{t}\:\left(\frac{{tdt}}{{t}^{\mathrm{2}\:} +\mathrm{25}}\right) \\ $$$$=\int\:\:\frac{{t}^{\mathrm{2}} \:{dt}}{{t}^{\mathrm{2}} \:+\mathrm{25}}\:=\int\:{dt}\:−\int\:\:\frac{\mathrm{25}{dt}}{{t}^{\mathrm{2}} \:+\mathrm{25}}\:={t}−\mathrm{25}\int\:\:\:\frac{{dt}}{{t}^{\mathrm{2}} +\mathrm{25}} \\ $$$$=_{{t}=\mathrm{5}{u}} \:\:\:\:{t}−\mathrm{25}\:\int\:\:\:\frac{\mathrm{5}{du}}{\mathrm{25}\left({u}^{\mathrm{2}} \:+\mathrm{1}\right)}\:={t}\:−\mathrm{5}\:{arctan}\left(\frac{{t}}{\mathrm{5}}\right)+{C} \\ $$$$=\sqrt{{x}^{\mathrm{2}} −\mathrm{25}}\:−\mathrm{5}{arctan}\left(\frac{\sqrt{{x}^{\mathrm{2}} −\mathrm{25}}}{\mathrm{5}}\right)\:+{C} \\ $$
Answered by john santu last updated on 27/Mar/20
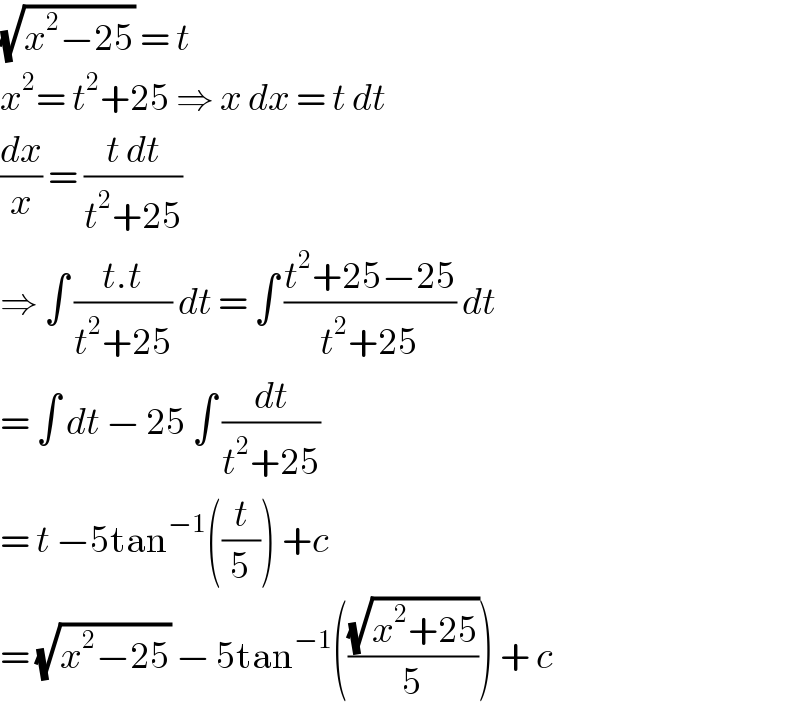
$$\sqrt{{x}^{\mathrm{2}} −\mathrm{25}}\:=\:{t} \\ $$$${x}^{\mathrm{2}} =\:{t}^{\mathrm{2}} +\mathrm{25}\:\Rightarrow\:{x}\:{dx}\:=\:{t}\:{dt} \\ $$$$\frac{{dx}}{{x}}\:=\:\frac{{t}\:{dt}}{{t}^{\mathrm{2}} +\mathrm{25}} \\ $$$$\Rightarrow\:\int\:\frac{{t}.{t}}{{t}^{\mathrm{2}} +\mathrm{25}}\:{dt}\:=\:\int\:\frac{{t}^{\mathrm{2}} +\mathrm{25}−\mathrm{25}}{{t}^{\mathrm{2}} +\mathrm{25}}\:{dt} \\ $$$$=\:\int\:{dt}\:−\:\mathrm{25}\:\int\:\frac{{dt}}{{t}^{\mathrm{2}} +\mathrm{25}} \\ $$$$=\:{t}\:−\mathrm{5tan}^{−\mathrm{1}} \left(\frac{{t}}{\mathrm{5}}\right)\:+{c} \\ $$$$=\:\sqrt{{x}^{\mathrm{2}} −\mathrm{25}}\:−\:\mathrm{5tan}^{−\mathrm{1}} \left(\frac{\sqrt{{x}^{\mathrm{2}} +\mathrm{25}}}{\mathrm{5}}\right)\:+\:{c} \\ $$
Commented by john santu last updated on 27/Mar/20

$${o}\:{yes}.\:{thank}\:{you} \\ $$$$ \\ $$
Commented by ar247 last updated on 26/Mar/20
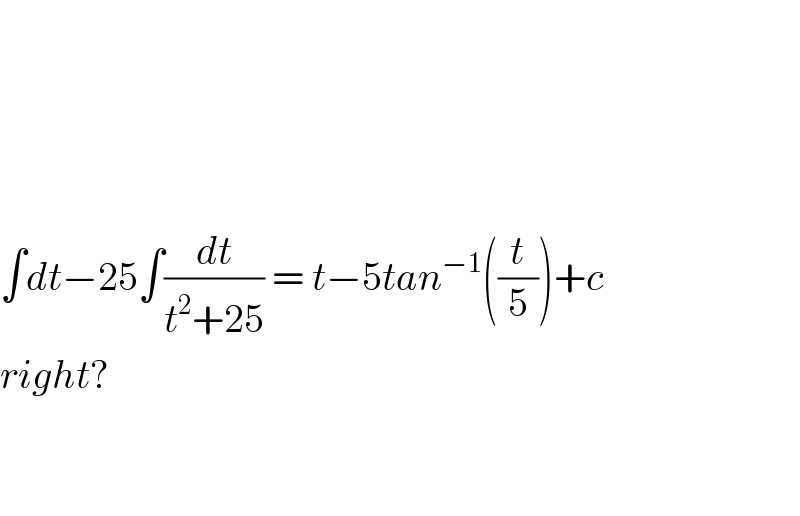
$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$\int{dt}−\mathrm{25}\int\frac{{dt}}{{t}^{\mathrm{2}} +\mathrm{25}}\:=\:{t}−\mathrm{5}{tan}^{−\mathrm{1}} \left(\frac{{t}}{\mathrm{5}}\right)+{c}\: \\ $$$${right}? \\ $$$$ \\ $$$$ \\ $$
Commented by jagoll last updated on 26/Mar/20
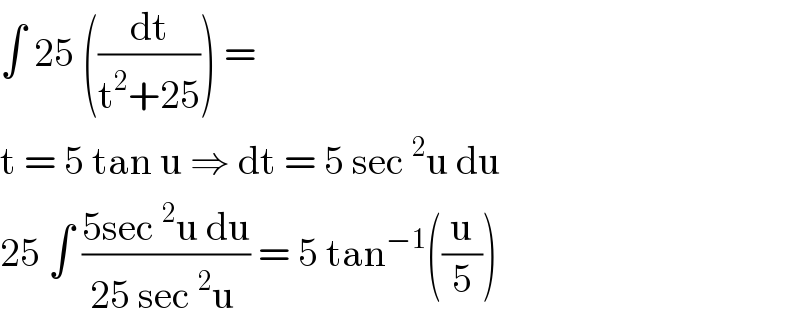
$$\int\:\mathrm{25}\:\left(\frac{\mathrm{dt}}{\mathrm{t}^{\mathrm{2}} +\mathrm{25}}\right)\:= \\ $$$$\mathrm{t}\:=\:\mathrm{5}\:\mathrm{tan}\:\mathrm{u}\:\Rightarrow\:\mathrm{dt}\:=\:\mathrm{5}\:\mathrm{sec}\:^{\mathrm{2}} \mathrm{u}\:\mathrm{du} \\ $$$$\mathrm{25}\:\int\:\frac{\mathrm{5sec}\:^{\mathrm{2}} \mathrm{u}\:\mathrm{du}}{\mathrm{25}\:\mathrm{sec}\:^{\mathrm{2}} \mathrm{u}\:}\:=\:\mathrm{5}\:\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{u}}{\mathrm{5}}\right) \\ $$
Commented by jagoll last updated on 26/Mar/20

$$\mathrm{sir}\:\mathrm{john}\:,\mathrm{typo}\:\mathrm{sir}\:\mathrm{in}\:\mathrm{line}\:\mathrm{6} \\ $$
Answered by Rio Michael last updated on 26/Mar/20
![∫((√(x^2 −25))/x) dx let x = (5/(cos θ)) ⇒ ((√(x^2 −25))/x) = sin x ∫((√(x^2 −25))/x) dx = 5∫((sin^2 θ)/(cos^2 θ)) dθ = 5∫tan^2 θ dθ = 5(tan θ − θ + k) ⇒ ∫((√(x^2 −25))/x)dx = 5 [ tan (arcos ((5/x)))−arcos((5/x)) + k]](Q86077.png)
$$\:\int\frac{\sqrt{{x}^{\mathrm{2}} −\mathrm{25}}}{{x}}\:{dx}\: \\ $$$$\mathrm{let}\:{x}\:=\:\frac{\mathrm{5}}{\mathrm{cos}\:\theta}\:\Rightarrow\:\:\frac{\sqrt{{x}^{\mathrm{2}} −\mathrm{25}}}{{x}}\:=\:\mathrm{sin}\:{x} \\ $$$$\int\frac{\sqrt{{x}^{\mathrm{2}} −\mathrm{25}}}{{x}}\:{dx}\:=\:\mathrm{5}\int\frac{\mathrm{sin}^{\mathrm{2}} \theta}{\mathrm{cos}^{\mathrm{2}} \theta}\:{d}\theta\:=\:\mathrm{5}\int\mathrm{tan}^{\mathrm{2}} \theta\:{d}\theta \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\mathrm{5}\left(\mathrm{tan}\:\theta\:−\:\theta\:+\:{k}\right)\: \\ $$$$\Rightarrow\:\int\frac{\sqrt{{x}^{\mathrm{2}} −\mathrm{25}}}{{x}}{dx}\:=\:\mathrm{5}\:\left[\:\mathrm{tan}\:\left(\mathrm{arcos}\:\left(\frac{\mathrm{5}}{{x}}\right)\right)−\mathrm{arcos}\left(\frac{\mathrm{5}}{{x}}\right)\:+\:{k}\right] \\ $$$$\: \\ $$
