Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 86034 by ar247 last updated on 26/Mar/20

∫(dx/(√(×^2 +4)))

$$\int\frac{{dx}}{\sqrt{×^{\mathrm{2}} +\mathrm{4}}} \\ $$

Answered by TANMAY PANACEA. last updated on 26/Mar/20

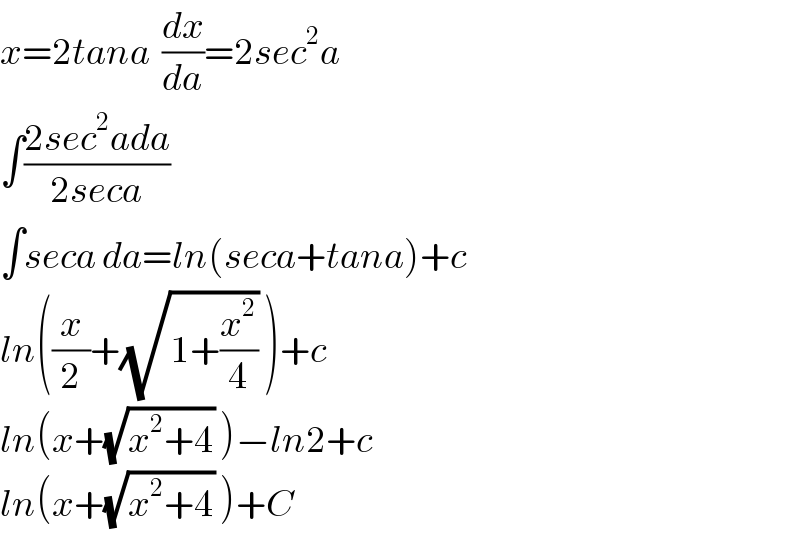
x=2tana (dx/da)=2sec^2 a ∫((2sec^2 ada)/(2seca)) ∫seca da=ln(seca+tana)+c ln((x/2)+(√(1+(x^2 /4))) )+c ln(x+(√(x^2 +4)) )−ln2+c ln(x+(√(x^2 +4)) )+C

$${x}=\mathrm{2}{tana}\:\:\frac{{dx}}{{da}}=\mathrm{2}{sec}^{\mathrm{2}} {a} \\ $$$$\int\frac{\mathrm{2}{sec}^{\mathrm{2}} {ada}}{\mathrm{2}{seca}} \\ $$$$\int{seca}\:{da}={ln}\left({seca}+{tana}\right)+{c} \\ $$$${ln}\left(\frac{{x}}{\mathrm{2}}+\sqrt{\mathrm{1}+\frac{{x}^{\mathrm{2}} }{\mathrm{4}}}\:\right)+{c} \\ $$$${ln}\left({x}+\sqrt{{x}^{\mathrm{2}} +\mathrm{4}}\:\right)−{ln}\mathrm{2}+{c} \\ $$$${ln}\left({x}+\sqrt{{x}^{\mathrm{2}} +\mathrm{4}}\:\right)+{C} \\ $$

Answered by Rio Michael last updated on 26/Mar/20

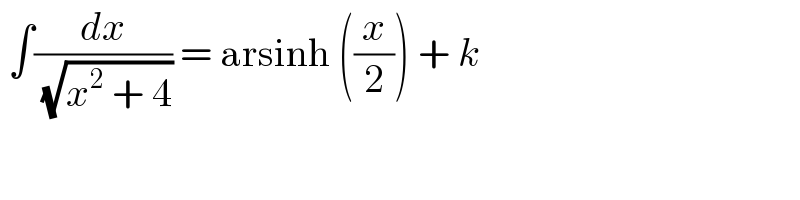
∫(dx/(√(x^2 + 4))) = arsinh ((x/2)) + k

$$\:\int\frac{{dx}}{\sqrt{{x}^{\mathrm{2}} \:+\:\mathrm{4}}}\:=\:\mathrm{arsinh}\:\left(\frac{{x}}{\mathrm{2}}\right)\:+\:{k}\: \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com