
Previous in Differential Equation Next in Differential Equation
Question Number 85835 by sahnaz last updated on 25/Mar/20
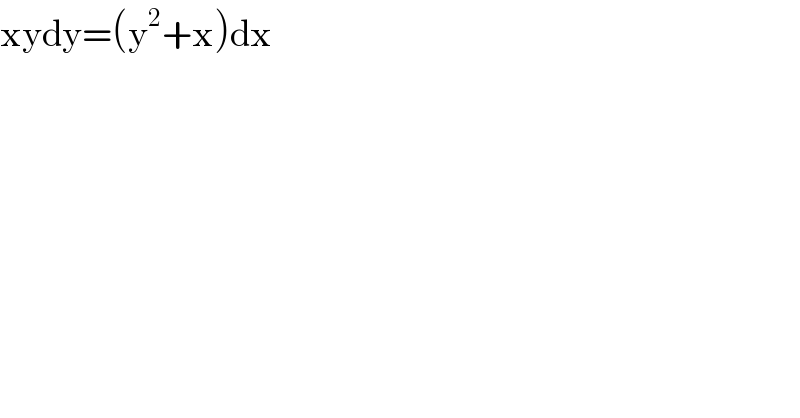
$$\mathrm{xydy}=\left(\mathrm{y}^{\mathrm{2}} +\mathrm{x}\right)\mathrm{dx} \\ $$
Answered by TANMAY PANACEA. last updated on 25/Mar/20
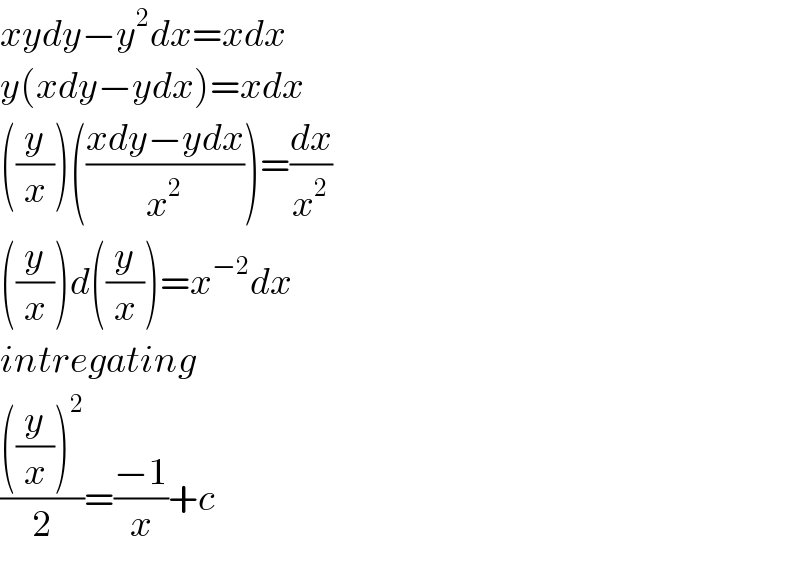
$${xydy}−{y}^{\mathrm{2}} {dx}={xdx} \\ $$$${y}\left({xdy}−{ydx}\right)={xdx} \\ $$$$\left(\frac{{y}}{{x}}\right)\left(\frac{{xdy}−{ydx}}{{x}^{\mathrm{2}} }\right)=\frac{{dx}}{{x}^{\mathrm{2}} } \\ $$$$\left(\frac{{y}}{{x}}\right){d}\left(\frac{{y}}{{x}}\right)={x}^{−\mathrm{2}} {dx} \\ $$$${intregating} \\ $$$$\frac{\left(\frac{{y}}{{x}}\right)^{\mathrm{2}} }{\mathrm{2}}=\frac{−\mathrm{1}}{{x}}+{c} \\ $$
Commented by sahnaz last updated on 25/Mar/20
$$\mathrm{thank}\:\mathrm{you}\:\mathrm{dear}\:\mathrm{friend} \\ $$
