
Question Number 84932 by jagoll last updated on 17/Mar/20
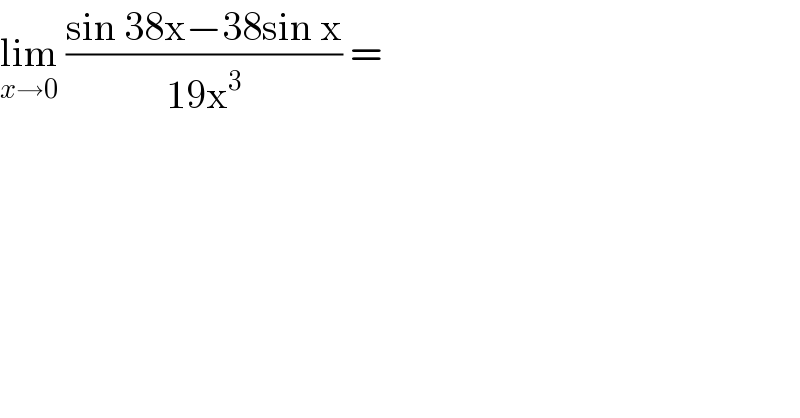
$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{sin}\:\mathrm{38x}−\mathrm{38sin}\:\mathrm{x}}{\mathrm{19x}^{\mathrm{3}} }\:=\: \\ $$
Commented by john santu last updated on 17/Mar/20
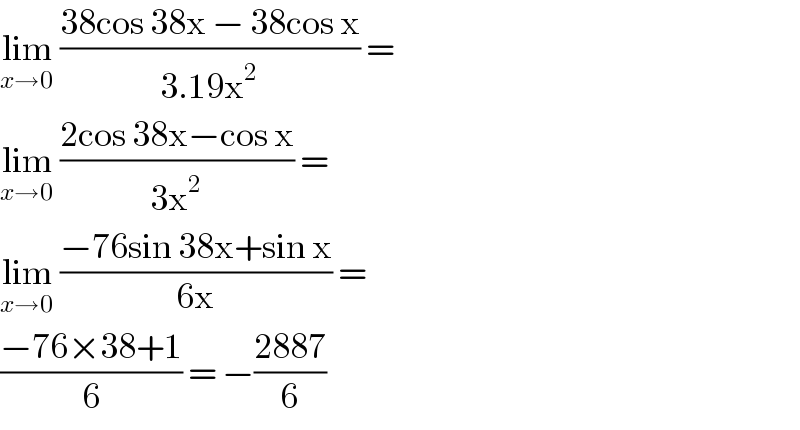
$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{38cos}\:\mathrm{38x}\:−\:\mathrm{38cos}\:\mathrm{x}}{\mathrm{3}.\mathrm{19x}^{\mathrm{2}} }\:= \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{2cos}\:\mathrm{38x}−\mathrm{cos}\:\mathrm{x}}{\mathrm{3x}^{\mathrm{2}} }\:=\: \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{−\mathrm{76sin}\:\mathrm{38x}+\mathrm{sin}\:\mathrm{x}}{\mathrm{6x}}\:= \\ $$$$\frac{−\mathrm{76}×\mathrm{38}+\mathrm{1}}{\mathrm{6}}\:=\:−\frac{\mathrm{2887}}{\mathrm{6}} \\ $$
