
Question Number 84564 by Rio Michael last updated on 14/Mar/20
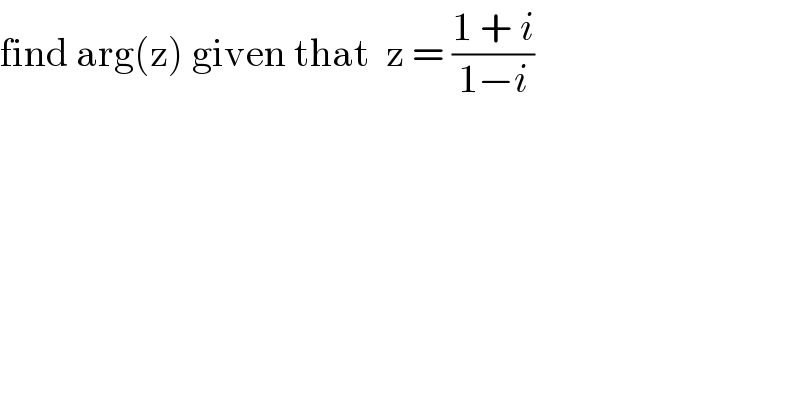
$$\mathrm{find}\:\mathrm{arg}\left(\mathrm{z}\right)\:\mathrm{given}\:\mathrm{that}\:\:\mathrm{z}\:=\:\frac{\mathrm{1}\:+\:{i}}{\mathrm{1}−{i}} \\ $$
Commented by mr W last updated on 14/Mar/20
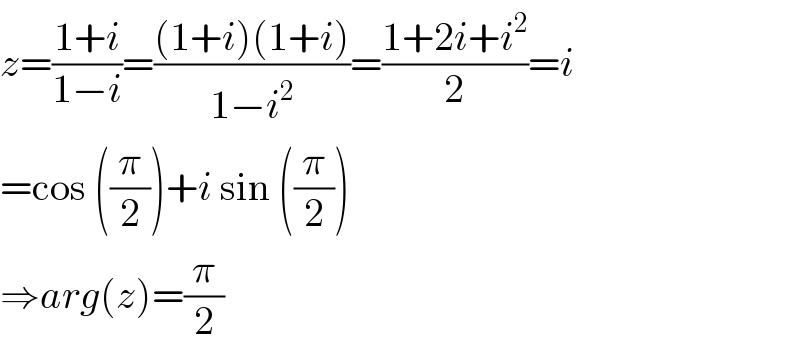
$${z}=\frac{\mathrm{1}+{i}}{\mathrm{1}−{i}}=\frac{\left(\mathrm{1}+{i}\right)\left(\mathrm{1}+{i}\right)}{\mathrm{1}−{i}^{\mathrm{2}} }=\frac{\mathrm{1}+\mathrm{2}{i}+{i}^{\mathrm{2}} }{\mathrm{2}}={i} \\ $$$$=\mathrm{cos}\:\left(\frac{\pi}{\mathrm{2}}\right)+{i}\:\mathrm{sin}\:\left(\frac{\pi}{\mathrm{2}}\right) \\ $$$$\Rightarrow{arg}\left({z}\right)=\frac{\pi}{\mathrm{2}} \\ $$
