Question and Answers Forum

All Questions      Topic List

Relation and Functions Questions

Previous in All Question      Next in All Question      

Previous in Relation and Functions      Next in Relation and Functions      

Question Number 84448 by jagoll last updated on 13/Mar/20

5^((x^2 −7∣x∣+10)/(x^2 −6x+9)) < 1

$$\mathrm{5}^{\frac{\mathrm{x}^{\mathrm{2}} −\mathrm{7}\mid\mathrm{x}\mid+\mathrm{10}}{\mathrm{x}^{\mathrm{2}} −\mathrm{6x}+\mathrm{9}}} \:<\:\mathrm{1} \\ $$

Answered by john santu last updated on 13/Mar/20

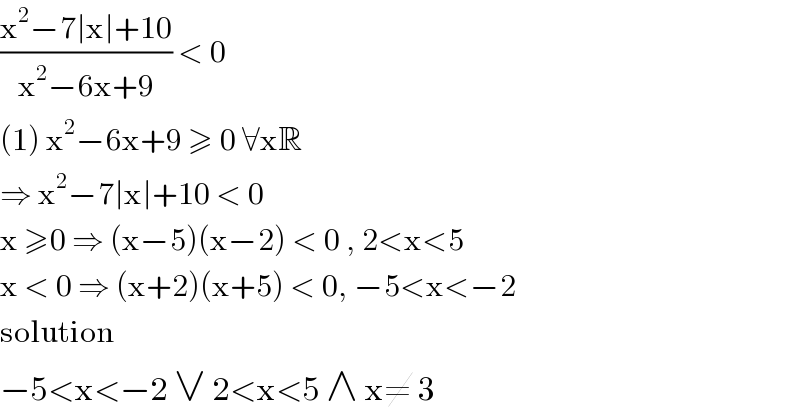
((x^2 −7∣x∣+10)/(x^2 −6x+9)) < 0 (1) x^2 −6x+9 ≥ 0 ∀xR ⇒ x^2 −7∣x∣+10 < 0 x ≥0 ⇒ (x−5)(x−2) < 0 , 2<x<5 x < 0 ⇒ (x+2)(x+5) < 0, −5<x<−2 solution −5<x<−2 ∨ 2<x<5 ∧ x≠ 3

$$\frac{\mathrm{x}^{\mathrm{2}} −\mathrm{7}\mid\mathrm{x}\mid+\mathrm{10}}{\mathrm{x}^{\mathrm{2}} −\mathrm{6x}+\mathrm{9}}\:<\:\mathrm{0} \\ $$ $$\left(\mathrm{1}\right)\:\mathrm{x}^{\mathrm{2}} −\mathrm{6x}+\mathrm{9}\:\geqslant\:\mathrm{0}\:\forall\mathrm{x}\mathbb{R} \\ $$ $$\Rightarrow\:\mathrm{x}^{\mathrm{2}} −\mathrm{7}\mid\mathrm{x}\mid+\mathrm{10}\:<\:\mathrm{0} \\ $$ $$\mathrm{x}\:\geqslant\mathrm{0}\:\Rightarrow\:\left(\mathrm{x}−\mathrm{5}\right)\left(\mathrm{x}−\mathrm{2}\right)\:<\:\mathrm{0}\:,\:\mathrm{2}<\mathrm{x}<\mathrm{5} \\ $$ $$\mathrm{x}\:<\:\mathrm{0}\:\Rightarrow\:\left(\mathrm{x}+\mathrm{2}\right)\left(\mathrm{x}+\mathrm{5}\right)\:<\:\mathrm{0},\:−\mathrm{5}<\mathrm{x}<−\mathrm{2} \\ $$ $$\mathrm{solution} \\ $$ $$−\mathrm{5}<\mathrm{x}<−\mathrm{2}\:\vee\:\mathrm{2}<\mathrm{x}<\mathrm{5}\:\wedge\:\mathrm{x}\neq\:\mathrm{3} \\ $$

Commented byjohn santu last updated on 13/Mar/20

l yes sir.i′m forgot

$$\mathrm{l}\:\mathrm{yes}\:\mathrm{sir}.\mathrm{i}'\mathrm{m}\:\mathrm{forgot} \\ $$

Commented byjagoll last updated on 13/Mar/20

thank you mister

$$\mathrm{thank}\:\mathrm{you}\:\mathrm{mister} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com