
Question Number 84442 by Power last updated on 13/Mar/20
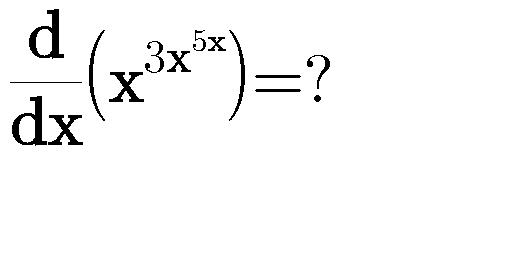
Answered by john santu last updated on 13/Mar/20
![let y = x^(3x^(5x) ) ⇒ln(y)= ln(x^(3x^(5x) ) ) let 3x^(5x) = g(x) ⇒ ln(y)= ln(x^(g(x)) ) ⇒ln(y) = g(x) ln(x) ⇒((y ′)/y) = ((g(x))/x) + g ′(x)ln(x) now consider g(x)= 3x^(5x) ln(g(x)) = ln(3x^(5x) ) = ln(3)+5x ln(x) ((g ′(x))/(g(x))) = 0+((5x)/x)+5ln(x) ((g ′(x))/(g(x)))= 5ln(ex) = ln(ex)^5 g ′(x)= 15x^(5x) ln(ex) now y′ = y [3x^(5x−1) +15xln(ex)ln(x) ] y ′ =x^(3x^(5x) ) [ 3x^(5x−1) + 15xln(ex) ln(x) ]](Q84444.png)
$$\mathrm{let}\:\mathrm{y}\:=\:\mathrm{x}^{\mathrm{3x}^{\mathrm{5x}} } \:\Rightarrow\mathrm{ln}\left(\mathrm{y}\right)=\:\mathrm{ln}\left(\mathrm{x}^{\mathrm{3x}^{\mathrm{5x}} } \right) \\ $$$$\mathrm{let}\:\mathrm{3x}^{\mathrm{5x}} \:=\:\mathrm{g}\left(\mathrm{x}\right) \\ $$$$\Rightarrow\:\mathrm{ln}\left(\mathrm{y}\right)=\:\mathrm{ln}\left(\mathrm{x}^{\mathrm{g}\left(\mathrm{x}\right)} \right)\: \\ $$$$\Rightarrow\mathrm{ln}\left(\mathrm{y}\right)\:=\:\mathrm{g}\left(\mathrm{x}\right)\:\mathrm{ln}\left(\mathrm{x}\right) \\ $$$$\Rightarrow\frac{\mathrm{y}\:'}{\mathrm{y}}\:=\:\frac{\mathrm{g}\left(\mathrm{x}\right)}{\mathrm{x}}\:+\:\mathrm{g}\:'\left(\mathrm{x}\right)\mathrm{ln}\left(\mathrm{x}\right) \\ $$$$\mathrm{now}\:\mathrm{consider}\:\mathrm{g}\left(\mathrm{x}\right)=\:\mathrm{3x}^{\mathrm{5x}} \\ $$$$\mathrm{ln}\left(\mathrm{g}\left(\mathrm{x}\right)\right)\:=\:\mathrm{ln}\left(\mathrm{3x}^{\mathrm{5x}} \right)\:=\:\mathrm{ln}\left(\mathrm{3}\right)+\mathrm{5x}\:\mathrm{ln}\left(\mathrm{x}\right) \\ $$$$\frac{\mathrm{g}\:'\left(\mathrm{x}\right)}{\mathrm{g}\left(\mathrm{x}\right)}\:=\:\mathrm{0}+\frac{\mathrm{5x}}{\mathrm{x}}+\mathrm{5ln}\left(\mathrm{x}\right) \\ $$$$\frac{\mathrm{g}\:'\left(\mathrm{x}\right)}{\mathrm{g}\left(\mathrm{x}\right)}=\:\mathrm{5ln}\left(\mathrm{ex}\right)\:=\:\mathrm{ln}\left(\mathrm{ex}\right)^{\mathrm{5}} \\ $$$$\mathrm{g}\:'\left(\mathrm{x}\right)=\:\mathrm{15x}^{\mathrm{5x}} \:\mathrm{ln}\left(\mathrm{ex}\right) \\ $$$$\mathrm{now}\:\mathrm{y}'\:=\:\mathrm{y}\:\left[\mathrm{3x}^{\mathrm{5x}−\mathrm{1}} +\mathrm{15xln}\left(\mathrm{ex}\right)\mathrm{ln}\left(\mathrm{x}\right)\:\right] \\ $$$$\mathrm{y}\:'\:=\mathrm{x}^{\mathrm{3x}^{\mathrm{5x}} } \:\left[\:\mathrm{3x}^{\mathrm{5x}−\mathrm{1}} \:+\:\mathrm{15xln}\left(\mathrm{ex}\right)\:\mathrm{ln}\left(\mathrm{x}\right)\:\right] \\ $$
