
Question Number 83110 by 09658867628 last updated on 28/Feb/20
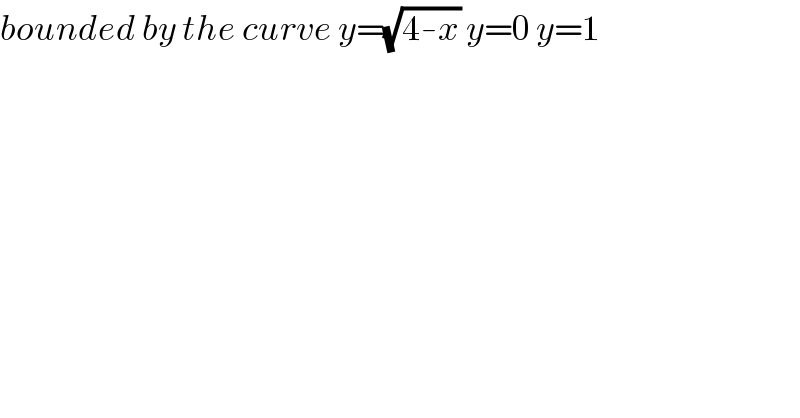
$${bounded}\:{by}\:{the}\:{curve}\:{y}=\sqrt{\mathrm{4}-{x}}\:{y}=\mathrm{0}\:{y}=\mathrm{1} \\ $$
Commented by jagoll last updated on 28/Feb/20
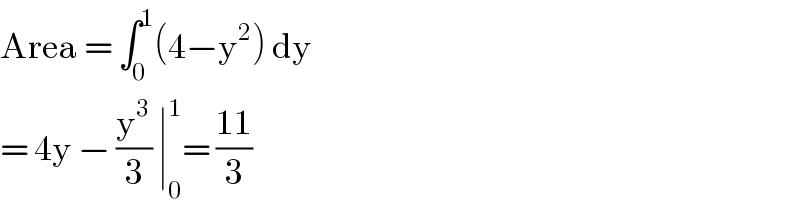
$$\mathrm{Area}\:=\:\int_{\mathrm{0}} ^{\mathrm{1}} \left(\mathrm{4}−\mathrm{y}^{\mathrm{2}} \right)\:\mathrm{dy}\: \\ $$$$=\:\mathrm{4y}\:−\:\frac{\mathrm{y}^{\mathrm{3}} }{\mathrm{3}}\:\mid_{\mathrm{0}} ^{\mathrm{1}} =\:\frac{\mathrm{11}}{\mathrm{3}} \\ $$
Commented by mr W last updated on 28/Feb/20
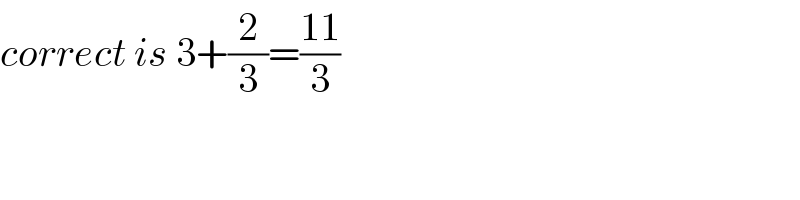
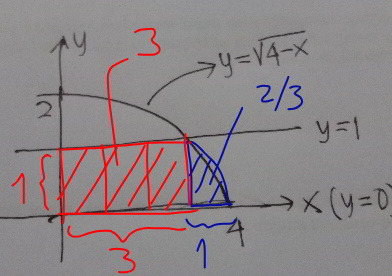
$${correct}\:{is}\:\mathrm{3}+\frac{\mathrm{2}}{\mathrm{3}}=\frac{\mathrm{11}}{\mathrm{3}} \\ $$
Commented by jagoll last updated on 28/Feb/20
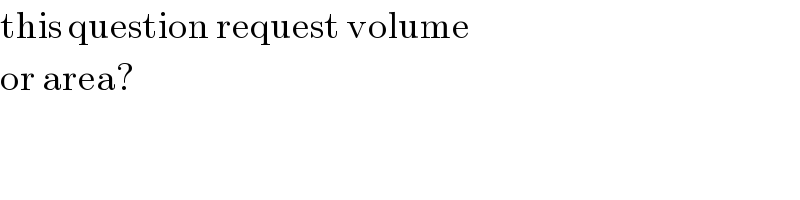
$$\mathrm{this}\:\mathrm{question}\:\mathrm{request}\:\mathrm{volume}\: \\ $$$$\mathrm{or}\:\mathrm{area}? \\ $$
Commented by mr W last updated on 28/Feb/20

$${area} \\ $$
Commented by jagoll last updated on 28/Feb/20
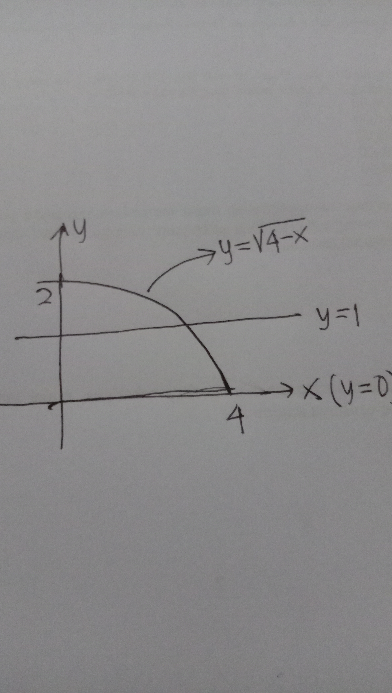
Commented by jagoll last updated on 28/Feb/20

$$\mathrm{where}\:\mathrm{this}\:\mathrm{area}\:? \\ $$
Commented by mr W last updated on 28/Feb/20

$${from}\:{y}=\mathrm{0}\:{to}\:{y}=\mathrm{1}. \\ $$$${not}\:{your}\:{method}\:{is}\:{wrong},\:{but}\:{your} \\ $$$${calculation}\:{is}\:{wrong}.\:{the}\:{result}\:{is} \\ $$$${not}\:\frac{\mathrm{8}}{\mathrm{3}},\:{but}\:\frac{\mathrm{11}}{\mathrm{3}}. \\ $$$$\int\left(\mathrm{4}−{y}^{\mathrm{2}} \right){dy}=\mathrm{4}{y}−\frac{{y}^{\mathrm{3}} }{\mathrm{3}}\neq\mathrm{4}{y}−\frac{\mathrm{4}{y}^{\mathrm{3}} }{\mathrm{3}} \\ $$$$ \\ $$$${but}\:{we}\:{can}\:{also}\:{get}\:{the}\:{result}\:{without} \\ $$$${integral},\:{the}\:{area}\:{is}\:\mathrm{3}+\frac{\mathrm{2}}{\mathrm{3}}=\frac{\mathrm{11}}{\mathrm{3}}. \\ $$
Commented by mr W last updated on 28/Feb/20
Commented by jagoll last updated on 28/Feb/20
$$\mathrm{hahaha}...\mathrm{yes}\:\mathrm{sir}.\:\mathrm{thank}\:\mathrm{you} \\ $$
Commented by jagoll last updated on 28/Feb/20
$$\mathrm{but}\:\mathrm{sir}.\:\mathrm{i}\:\mathrm{think}\:\mathrm{this}\:\mathrm{question}\:\mathrm{not}\: \\ $$$$\mathrm{complet}.\:\mathrm{my}\:\mathrm{understand}\:\mathrm{the}\:\mathrm{question} \\ $$$$\mathrm{must}\:\mathrm{be}\:\mathrm{the}\:\mathrm{area}\:\mathrm{bounded}\:\mathrm{the}\: \\ $$$$\mathrm{curve}\:\mathrm{y}\:=\:\sqrt{\mathrm{4}−\mathrm{x}}\:,\:\mathrm{y}=\mathrm{0}\:,\:\mathrm{y}=\mathrm{1}\:,\:\mathrm{x}\:=\:\mathrm{0} \\ $$
