Question Number 82185 by jagoll last updated on 19/Feb/20
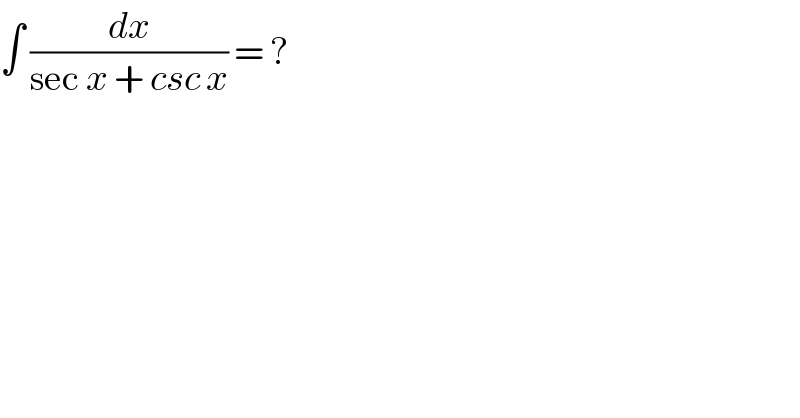
$$\int\:\frac{{dx}}{\mathrm{sec}\:{x}\:+\:{csc}\:{x}}\:=\:?\: \\ $$
Commented by john santu last updated on 19/Feb/20
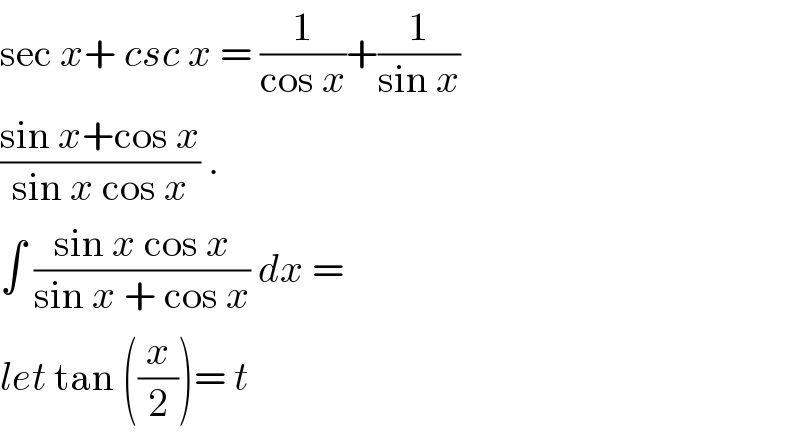
$$\mathrm{sec}\:{x}+\:{csc}\:{x}\:=\:\frac{\mathrm{1}}{\mathrm{cos}\:{x}}+\frac{\mathrm{1}}{\mathrm{sin}\:{x}} \\ $$$$\frac{\mathrm{sin}\:{x}+\mathrm{cos}\:{x}}{\mathrm{sin}\:{x}\:\mathrm{cos}\:{x}}\:. \\ $$$$\int\:\frac{\mathrm{sin}\:{x}\:\mathrm{cos}\:{x}}{\mathrm{sin}\:{x}\:+\:\mathrm{cos}\:{x}}\:{dx}\:=\: \\ $$$${let}\:\mathrm{tan}\:\left(\frac{{x}}{\mathrm{2}}\right)=\:{t}\: \\ $$
Commented by mathmax by abdo last updated on 19/Feb/20

$${let}\:\:{I}\:=\int\:\:\:\frac{{dx}}{\frac{\mathrm{1}}{{cosx}}\:+\frac{\mathrm{1}}{{sinx}}}\:\Rightarrow{I}\:=\int\:\:\frac{{cosx}\:.{sinx}}{{cosx}\:+{sinx}}{dx}\:\:{changement} \\ $$$${tan}\left(\frac{{x}}{\mathrm{2}}\right)={t}\:{give}\:{I}\:=\int\:\frac{\frac{\mathrm{1}−{t}^{\mathrm{2}} }{\mathrm{1}+{t}^{\mathrm{2}} }×\frac{\mathrm{2}{t}}{\mathrm{1}+{t}^{\mathrm{2}} }}{\frac{\mathrm{1}−{t}^{\mathrm{2}} }{\mathrm{1}+{t}^{\mathrm{2}} }+\frac{\mathrm{2}{t}}{\mathrm{1}+{t}^{\mathrm{2}} }}×\frac{\mathrm{2}{dt}}{\mathrm{1}+{t}^{\mathrm{2}} }\:=\int\frac{\mathrm{2}{t}\left(\mathrm{1}−{t}^{\mathrm{2}} \right)}{\left(\mathrm{1}+{t}^{\mathrm{2}} \right)^{\mathrm{2}} \left(−{t}^{\mathrm{2}} \:+\mathrm{2}{t}+\mathrm{1}\right)}{dt} \\ $$$$=\int\:\:\frac{\mathrm{2}{t}\left({t}^{\mathrm{2}} −\mathrm{1}\right)}{\left({t}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} \left({t}^{\mathrm{2}} −\mathrm{2}{t}−\mathrm{1}\right)}{dt}\:=\int\:\:\frac{\mathrm{2}{t}^{\mathrm{3}} −\mathrm{2}{t}}{\left({t}^{\mathrm{2}} \:+\mathrm{1}\right)^{\mathrm{2}} \left({t}^{\mathrm{2}} −\mathrm{2}{t}\:−\mathrm{1}\right)}{dt} \\ $$$${t}^{\mathrm{2}} −\mathrm{2}{t}−\mathrm{1}\:=\mathrm{0}\rightarrow\Delta^{'} =\mathrm{1}+\mathrm{1}=\mathrm{2}\:\Rightarrow{t}_{\mathrm{1}} =\mathrm{1}+\sqrt{\mathrm{2}}{and}\:{t}_{\mathrm{2}} =\mathrm{1}−\sqrt{\mathrm{2}}\:\:{let}\:{decompose} \\ $$$${F}\left({t}\right)=\frac{\mathrm{2}{t}^{\mathrm{3}} −\mathrm{2}{t}}{\left({t}^{\mathrm{2}} \:+\mathrm{1}\right)^{\mathrm{2}} \left({t}−{t}_{\mathrm{1}} \right)\left({t}−{t}_{\mathrm{2}} \right)}\:\Rightarrow{F}\left({t}\right)=\frac{{a}}{{t}−{t}_{\mathrm{1}} }\:+\frac{{b}}{{t}−{t}_{\mathrm{2}} }\:+\frac{{ct}\:+{d}}{{t}^{\mathrm{2}} \:+\mathrm{1}}\:+\frac{{et}\:+{f}}{\left({t}^{\mathrm{2}} \:+\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$\Rightarrow\int\:{F}\left({t}\right){dt}\:={aln}\mid{t}−{t}_{\mathrm{1}} \mid+{bln}\mid{t}−{t}_{\mathrm{2}} \mid\:+\frac{{c}}{\mathrm{2}}{ln}\left({t}^{\mathrm{2}} \:+\mathrm{1}\right)+{d}\:{arctan}\left({t}\right) \\ $$$$+\int\:\frac{{et}\:+{f}}{\left({t}^{\mathrm{2}} \:+\mathrm{1}\right)^{\mathrm{2}} }{dt}\:\:{rest}\:{calculus}\:{of}\:{coefficients}\:...{be}\:{continued}... \\ $$$$ \\ $$
Answered by TANMAY PANACEA last updated on 20/Feb/20
![∫((sinx+cosx)/(sinxcosx))dx 2∫((sinx+cosx)/(1−(1−2sinxcosx)))dx 2∫((d(sinx−cosx))/(1−(sinx−cosx)^2 )) [formula ∫(da/(1−a^2 ))] ln(((sinx−cosx+1)/(sinx−cosx−1)))+c](Q82297.png)
$$\int\frac{{sinx}+{cosx}}{{sinxcosx}}{dx} \\ $$$$\mathrm{2}\int\frac{{sinx}+{cosx}}{\mathrm{1}−\left(\mathrm{1}−\mathrm{2}{sinxcosx}\right)}{dx} \\ $$$$\mathrm{2}\int\frac{{d}\left({sinx}−{cosx}\right)}{\mathrm{1}−\left({sinx}−{cosx}\right)^{\mathrm{2}} }\:\left[{formula}\:\int\frac{{da}}{\mathrm{1}−{a}^{\mathrm{2}} }\right] \\ $$$${ln}\left(\frac{{sinx}−{cosx}+\mathrm{1}}{{sinx}−{cosx}−\mathrm{1}}\right)+{c} \\ $$
Commented by jagoll last updated on 20/Feb/20
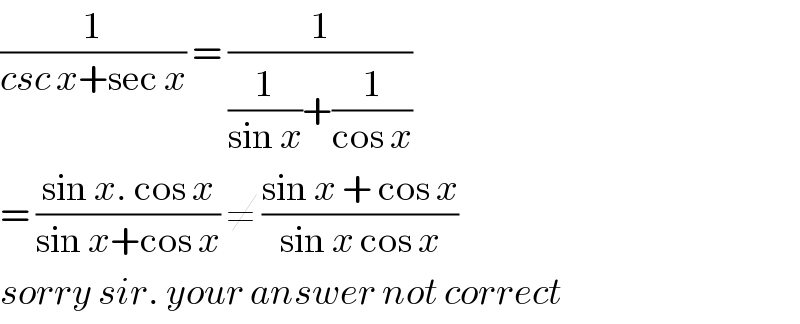
$$\frac{\mathrm{1}}{{csc}\:{x}+\mathrm{sec}\:{x}}\:=\:\frac{\mathrm{1}}{\frac{\mathrm{1}}{\mathrm{sin}\:{x}}+\frac{\mathrm{1}}{\mathrm{cos}\:{x}}} \\ $$$$=\:\frac{\mathrm{sin}\:{x}.\:\mathrm{cos}\:{x}}{\mathrm{sin}\:{x}+\mathrm{cos}\:{x}}\:\neq\:\frac{\mathrm{sin}\:{x}\:+\:\mathrm{cos}\:{x}}{\mathrm{sin}\:{x}\:\mathrm{cos}\:{x}} \\ $$$${sorry}\:{sir}.\:{your}\:{answer}\:{not}\:{correct} \\ $$
Commented by TANMAY PANACEA last updated on 20/Feb/20