
Previous in Relation and Functions Next in Relation and Functions
Question Number 81720 by mathmax by abdo last updated on 14/Feb/20
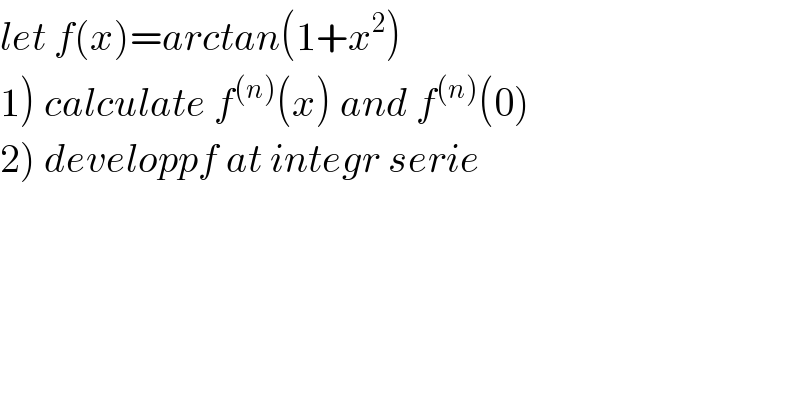
$${let}\:{f}\left({x}\right)={arctan}\left(\mathrm{1}+{x}^{\mathrm{2}} \right) \\ $$$$\left.\mathrm{1}\right)\:{calculate}\:{f}^{\left({n}\right)} \left({x}\right)\:{and}\:{f}^{\left({n}\right)} \left(\mathrm{0}\right) \\ $$$$\left.\mathrm{2}\right)\:{developpf}\:{at}\:{integr}\:{serie} \\ $$
Commented by mathmax by abdo last updated on 15/Feb/20

$$\left.\mathrm{1}\right)\:{we}\:{have}\:{f}^{'} \left({x}\right)=\frac{\mathrm{2}{x}}{\mathrm{1}+\left(\mathrm{1}+{x}^{\mathrm{2}} \right)^{\mathrm{2}} }\:=\frac{\mathrm{2}{x}}{\mathrm{1}+{x}^{\mathrm{4}} \:+\mathrm{2}{x}^{\mathrm{2}} \:+\mathrm{1}}\:=\frac{\mathrm{2}{x}}{{x}^{\mathrm{4}} \:+\mathrm{2}{x}^{\mathrm{2}} \:+\mathrm{2}} \\ $$$${x}^{\mathrm{4}} \:+\mathrm{2}{x}^{\mathrm{2}} +\mathrm{2}=\mathrm{0}\:\rightarrow{t}^{\mathrm{2}} +\mathrm{2}{t}\:+\mathrm{2}=\mathrm{0}\:\:\left({t}={x}^{\mathrm{2}} \right)\rightarrow\Delta^{'} =\mathrm{1}−\mathrm{2}=−\mathrm{1}\:\Rightarrow \\ $$$${x}_{\mathrm{1}} =−\mathrm{1}+{i}\:\:=\sqrt{\mathrm{2}}{e}^{{i}\frac{\mathrm{3}\pi}{\mathrm{4}}} \:\:{and}\:{x}_{\mathrm{2}} =−\mathrm{1}−{i}\:=\sqrt{\mathrm{2}}{e}^{−\frac{{i}\mathrm{3}\pi}{\mathrm{4}}} \:\Rightarrow \\ $$$${f}^{'} \left({x}\right)=\frac{\mathrm{2}{x}}{\left({x}^{\mathrm{2}} −\sqrt{\mathrm{2}}{e}^{\frac{{i}\mathrm{3}\pi}{\mathrm{4}}} \right)\left({x}^{\mathrm{2}} −\sqrt{\mathrm{2}}{e}^{−\frac{{i}\mathrm{3}\pi}{\mathrm{4}}} \right)}\:=\frac{\mathrm{2}{x}}{\left({x}−\alpha{e}^{\frac{{i}\mathrm{3}\pi}{\mathrm{8}}} \right)\left({x}+\alpha\:{e}^{\frac{{i}\mathrm{3}\pi}{\mathrm{8}}} \right)\left({x}−\alpha\:{e}^{−\frac{{i}\mathrm{3}\pi}{\mathrm{8}}} \right)\left({x}+\alpha\:{e}^{−\frac{{i}\mathrm{3}\pi}{\mathrm{8}}} \mathrm{3}\right.} \\ $$$$=\frac{{a}}{{x}−\alpha\:{e}^{\frac{{i}\mathrm{3}\pi}{\mathrm{8}}} }\:+\frac{{b}}{{x}+\alpha\:{e}^{\frac{{i}\mathrm{3}\pi}{\mathrm{8}}} }\:+\frac{{c}}{{x}−\alpha\:{e}^{−{i}\frac{\mathrm{3}\pi}{\mathrm{8}}} }\:+\frac{{d}}{\left({x}\:+{e}^{−\frac{{i}\mathrm{3}\pi}{\mathrm{8}}} \right)}\:\:\:\left(\alpha=\sqrt{\sqrt{\mathrm{2}}}\right) \\ $$$${a}\:=\frac{\mathrm{2}\alpha\:{e}^{\frac{{i}\mathrm{3}\pi}{\mathrm{8}}} }{\mathrm{2}\alpha\:{e}^{\frac{{i}\mathrm{3}\pi}{\mathrm{8}}} \sqrt{\mathrm{2}}\:\left(\mathrm{2}{i}\right)×\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}}\:=\frac{\mathrm{1}}{\mathrm{2}{i}} \\ $$$${b}=\frac{−\mathrm{2}\alpha\:{e}^{\frac{{i}\mathrm{3}\pi}{\mathrm{8}}} }{−\mathrm{2}\alpha\:{e}^{\frac{{i}\mathrm{3}\pi}{\mathrm{8}}} \sqrt{\mathrm{2}}\left(\mathrm{2}{i}\right)×\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}}\:=\frac{\mathrm{1}}{\mathrm{2}{i}} \\ $$$${c}\:=\frac{\mathrm{2}\alpha\:{e}^{−\frac{{i}\mathrm{3}\pi}{\mathrm{8}}} }{\mathrm{2}\alpha\:{e}^{−\frac{{i}\mathrm{3}\pi}{\mathrm{8}}} \sqrt{\mathrm{2}}\left(−\mathrm{2}{i}\right)×\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}}\:=−\frac{\mathrm{1}}{\mathrm{2}{i}} \\ $$$${d}\:=\frac{−\mathrm{2}\alpha\:{e}^{−\frac{{i}\mathrm{3}\pi}{\mathrm{8}}} }{−\mathrm{2}\alpha\:{e}^{−\frac{{i}\mathrm{3}\pi}{\mathrm{8}}} \sqrt{\mathrm{2}}\left(−\mathrm{2}{i}\right)×\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}}\:=−\frac{\mathrm{1}}{\mathrm{2}{i}}\:\Rightarrow \\ $$$${f}^{'} \left({x}\right)\:=\frac{\mathrm{1}}{\mathrm{2}{i}}\left\{\:\:\frac{\mathrm{1}}{{x}−\alpha\:{e}^{\frac{{i}\mathrm{3}\pi}{\mathrm{8}}} }\:+\frac{\mathrm{1}}{{x}+\alpha\:{e}^{\frac{{i}\mathrm{3}\pi}{\mathrm{8}}} }\:−\frac{\mathrm{1}}{{x}−\alpha\:{e}^{−\frac{{i}\mathrm{3}\pi}{\mathrm{8}}} }−\frac{\mathrm{1}}{{x}+\alpha\:{e}^{−\frac{{i}\mathrm{3}\pi}{\mathrm{8}}} }\right\}\:\Rightarrow \\ $$$${f}^{\left({n}\right)} \left({x}\right)\:=\frac{\mathrm{1}}{\mathrm{2}{i}}\left\{\:\:\frac{\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} \left({n}−\mathrm{1}\right)!}{\left({x}−\alpha\:{e}^{\frac{{i}\mathrm{3}\pi}{\mathrm{8}}} \right)^{{n}} }\:+\frac{\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} \left({n}−\mathrm{1}\right)!}{\left({x}+\alpha\:{e}^{\frac{{i}\mathrm{3}\pi}{\mathrm{8}}} \right)^{{n}} }\right. \\ $$$$\left.−\frac{\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} \left({n}−\mathrm{1}\right)!}{\left({x}−\alpha{e}^{−\frac{{i}\mathrm{3}\pi}{\mathrm{8}}} \right)^{{n}} }−\frac{\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} \left({n}−\mathrm{1}\right)!}{\left({x}+\alpha{e}^{−\frac{{i}\mathrm{3}\pi}{\mathrm{8}}} \right)^{{n}} }\right\} \\ $$$$=\frac{\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} \left({n}−\mathrm{1}\right)!}{\mathrm{2}{i}}\left\{\frac{\mathrm{1}}{\left({x}−\alpha\:{e}^{\frac{{i}\mathrm{3}\pi}{\mathrm{8}}} \right)^{{n}} }−\frac{\mathrm{1}}{\left({x}−\alpha\:{e}^{−\frac{{i}\mathrm{3}\pi}{\mathrm{8}}} \right)^{{n}} }\:+\frac{\mathrm{1}}{\left({x}+\alpha\:{e}^{−\frac{{i}\mathrm{3}\pi}{\mathrm{8}}} \right)^{{n}} }\right. \\ $$$$\left.−\frac{\mathrm{1}}{\left({x}\:+\alpha\:{e}^{−\frac{{i}\mathrm{3}\pi}{\mathrm{8}}} \right)^{{n}} }\right\} \\ $$$$=\frac{\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} \left({n}−\mathrm{1}\right)!}{\mathrm{2}{i}}\left\{\frac{−\mathrm{2}{i}\:{Im}\left({x}−\alpha\:{e}^{−\frac{{i}\mathrm{3}\pi}{\mathrm{8}}} \right)^{{n}} }{\left({x}^{\mathrm{2}} −\mathrm{2}\alpha\:{cos}\left(\frac{\mathrm{3}\pi}{\mathrm{8}}\right){x}\:+\alpha^{\mathrm{2}} \right)^{{n}} }\:+\frac{−\mathrm{2}{i}\:{Im}\left({x}+\alpha\:{e}^{−\frac{{i}\mathrm{3}\pi}{\mathrm{8}}} \right)^{{n}} }{\left({x}^{\mathrm{2}} \:+\mathrm{2}\alpha\:{cos}\left(\frac{\mathrm{3}\pi}{\mathrm{8}}\right){x}\:+\alpha^{\mathrm{2}} \right)^{{n}} }\right\} \\ $$$${f}^{\left({n}\right)} \left({x}\right)=\left(−\mathrm{1}\right)^{{n}} \left({n}−\mathrm{1}\right)!\left\{\frac{{Im}\left({x}−\alpha\:{e}^{−\frac{{i}\mathrm{3}\pi}{\mathrm{8}}} \right)^{{n}} }{\left({x}^{\mathrm{2}} −\mathrm{2}\alpha\:{cos}\left(\frac{\mathrm{3}\pi}{\mathrm{8}}\right){x}\:+\alpha^{\mathrm{2}} \right)^{{n}} }\:+\frac{{Im}\left({x}+\alpha{e}^{−\frac{{i}\mathrm{3}\pi}{\mathrm{8}}} \right)^{{n}} }{\left({x}^{\mathrm{2}} \:+\mathrm{2}\alpha\:{cos}\left(\frac{\mathrm{3}\pi}{\mathrm{8}}\right){x}+\alpha^{\mathrm{2}} \right)^{{n}} }\right\} \\ $$
Commented by mathmax by abdo last updated on 15/Feb/20
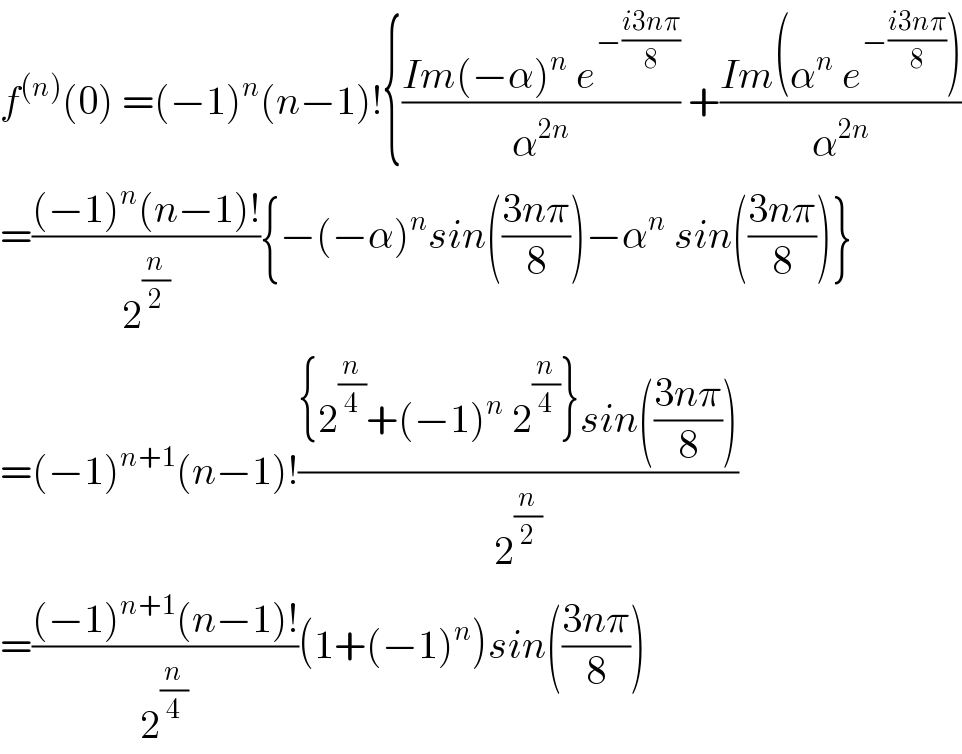
$${f}^{\left({n}\right)} \left(\mathrm{0}\right)\:=\left(−\mathrm{1}\right)^{{n}} \left({n}−\mathrm{1}\right)!\left\{\frac{{Im}\left(−\alpha\right)^{{n}} \:{e}^{−\frac{{i}\mathrm{3}{n}\pi}{\mathrm{8}}} }{\alpha^{\mathrm{2}{n}} }\:+\frac{{Im}\left(\alpha^{{n}} \:{e}^{−\frac{{i}\mathrm{3}{n}\pi}{\mathrm{8}}} \right)}{\alpha^{\mathrm{2}{n}} }\right. \\ $$$$=\frac{\left(−\mathrm{1}\right)^{{n}} \left({n}−\mathrm{1}\right)!}{\mathrm{2}^{\frac{{n}}{\mathrm{2}}} }\left\{−\left(−\alpha\right)^{{n}} {sin}\left(\frac{\mathrm{3}{n}\pi}{\mathrm{8}}\right)−\alpha^{{n}} \:{sin}\left(\frac{\mathrm{3}{n}\pi}{\mathrm{8}}\right)\right\} \\ $$$$=\left(−\mathrm{1}\right)^{{n}+\mathrm{1}} \left({n}−\mathrm{1}\right)!\frac{\left\{\mathrm{2}^{\frac{{n}}{\mathrm{4}}} +\left(−\mathrm{1}\right)^{{n}} \:\mathrm{2}^{\frac{{n}}{\mathrm{4}}} \right\}{sin}\left(\frac{\mathrm{3}{n}\pi}{\mathrm{8}}\right)}{\mathrm{2}^{\frac{{n}}{\mathrm{2}}} } \\ $$$$=\frac{\left(−\mathrm{1}\right)^{{n}+\mathrm{1}} \left({n}−\mathrm{1}\right)!}{\mathrm{2}^{\frac{{n}}{\mathrm{4}}} }\left(\mathrm{1}+\left(−\mathrm{1}\right)^{{n}} \right){sin}\left(\frac{\mathrm{3}{n}\pi}{\mathrm{8}}\right) \\ $$
