
Question Number 81648 by Zainal Arifin last updated on 14/Feb/20

$$\mathrm{A}\:\mathrm{team}\:\mathrm{of}\:\mathrm{8}\:\mathrm{couples},\:\left(\mathrm{husband}\:\mathrm{and}\:\mathrm{wife}\right) \\ $$$$\mathrm{attend}\:\mathrm{a}\:\mathrm{lucky}\:\mathrm{draw}\:\mathrm{in}\:\mathrm{which}\:\mathrm{4}\:\mathrm{persons} \\ $$$$\mathrm{picked}\:\mathrm{up}\:\mathrm{for}\:\mathrm{a}\:\mathrm{prize}.\:\mathrm{Then}\:\mathrm{the}\:\mathrm{probability} \\ $$$$\mathrm{that}\:\mathrm{there}\:\mathrm{is}\:\mathrm{at}\:\mathrm{least}\:\mathrm{one}\:\mathrm{couple}\:\mathrm{is} \\ $$
Commented by mr W last updated on 14/Feb/20
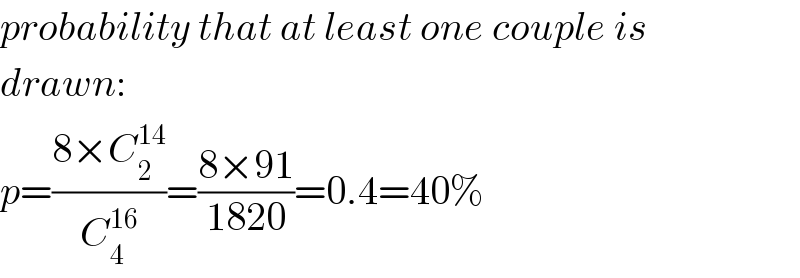
$${probability}\:{that}\:{at}\:{least}\:{one}\:{couple}\:{is} \\ $$$${drawn}: \\ $$$${p}=\frac{\mathrm{8}×{C}_{\mathrm{2}} ^{\mathrm{14}} }{{C}_{\mathrm{4}} ^{\mathrm{16}} }=\frac{\mathrm{8}×\mathrm{91}}{\mathrm{1820}}=\mathrm{0}.\mathrm{4}=\mathrm{40\%} \\ $$
Commented by mr W last updated on 14/Feb/20
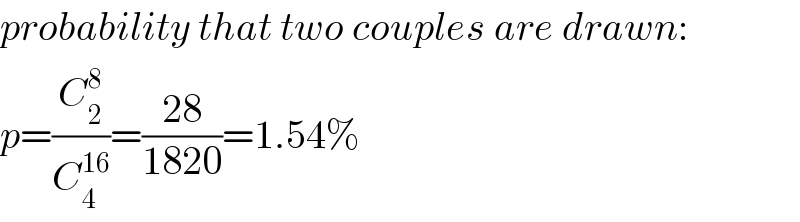
$${probability}\:{that}\:{two}\:{couples}\:{are}\:{drawn}: \\ $$$${p}=\frac{{C}_{\mathrm{2}} ^{\mathrm{8}} }{{C}_{\mathrm{4}} ^{\mathrm{16}} }=\frac{\mathrm{28}}{\mathrm{1820}}=\mathrm{1}.\mathrm{54\%} \\ $$
