
Previous in Relation and Functions Next in Relation and Functions
Question Number 81428 by abdomathmax last updated on 13/Feb/20
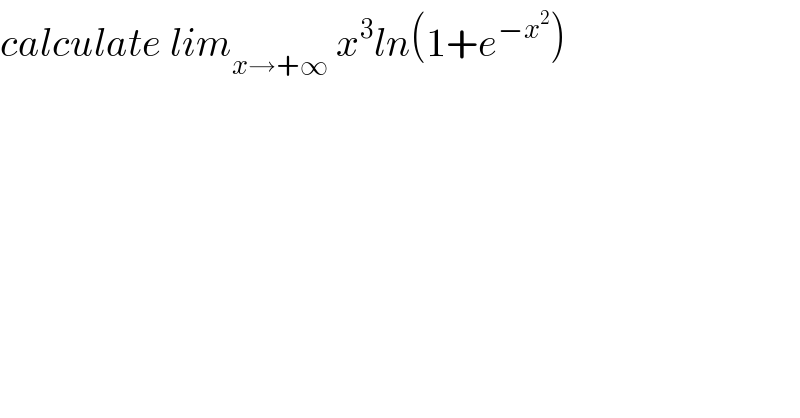
$${calculate}\:{lim}_{{x}\rightarrow+\infty} \:{x}^{\mathrm{3}} {ln}\left(\mathrm{1}+{e}^{−{x}^{\mathrm{2}} } \right) \\ $$
Answered by mind is power last updated on 13/Feb/20

$${ln}\left(\mathrm{1}+{e}^{−{x}^{\mathrm{2}} } \right)\sim{e}^{−{x}^{\mathrm{2}} } \\ $$$${x}^{\mathrm{3}} {ln}\left(\mathrm{1}+{e}^{−{x}^{\mathrm{2}} } \right)\rightarrow\mathrm{0} \\ $$
