
Question Number 81400 by mind is power last updated on 12/Feb/20

$${Hello}\:\:{Nice}\:{day}\:{im}\:{thinking}\:{of}\:{this}\:{one}\:\:{a}\:{close}\:{forme}? \\ $$$$\int\sqrt{\mathrm{1}+{x}^{{p}} }{dx} \\ $$$${p}\in\mathbb{R}_{+} , \\ $$$${x}\in\left[\mathrm{0},\mathrm{1}\left[\right.\right. \\ $$
Commented by abdomathmax last updated on 13/Feb/20

$${at}\:{form}\:{of}\:{serie}\:{we}\:{have}\: \\ $$$$\left(\mathrm{1}+{u}\right)^{\alpha} =\mathrm{1}+\frac{\alpha}{\mathrm{1}!}{u}\:+\frac{\alpha\left(\alpha−\mathrm{1}\right)}{\mathrm{2}!}{u}^{\mathrm{2}} +... \\ $$$$=\mathrm{1}+\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{\alpha\left(\alpha−\mathrm{1}\right)...\left(\alpha−{n}+\mathrm{1}\right)}{{n}!}\:{u}^{{n}} \:\Rightarrow \\ $$$$\sqrt{\mathrm{1}+{u}}=\mathrm{1}+\sum_{{n}=\mathrm{1}} ^{\infty} \frac{\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\mathrm{1}}{\mathrm{2}}−\mathrm{1}\right)....\left(\frac{\mathrm{1}}{\mathrm{2}}−{n}+\mathrm{1}\right)}{{n}!}{u}^{{n}} \:\Rightarrow \\ $$$$\sqrt{\mathrm{1}+{x}^{{p}} }=\mathrm{1}+\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\mathrm{1}}{\mathrm{2}}−\mathrm{1}\right)...\left(\frac{\mathrm{1}}{\mathrm{2}}−{n}+\mathrm{1}\right)}{{n}!}{x}^{{pn}} \:\Rightarrow \\ $$$$\int\sqrt{\mathrm{1}+{x}^{{p}} }{dx}= \\ $$$$\mathrm{1}+\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\mathrm{1}}{\mathrm{2}}−\mathrm{1}\right)...\left(\frac{\mathrm{1}}{\mathrm{2}}−{n}+\mathrm{1}\right)}{{n}!}×\frac{\mathrm{1}}{{pn}+\mathrm{1}}{x}^{{pn}+\mathrm{1}} \:+{C} \\ $$
Commented by mind is power last updated on 14/Feb/20
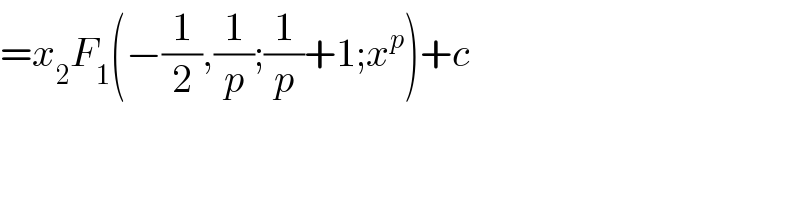
$$={x}_{\mathrm{2}} {F}_{\mathrm{1}} \left(−\frac{\mathrm{1}}{\mathrm{2}},\frac{\mathrm{1}}{{p}};\frac{\mathrm{1}}{{p}}+\mathrm{1};{x}^{{p}} \right)+{c} \\ $$
Commented by mind is power last updated on 14/Feb/20

$${nice}\:{Sir} \\ $$
Answered by behi83417@gmail.com last updated on 12/Feb/20
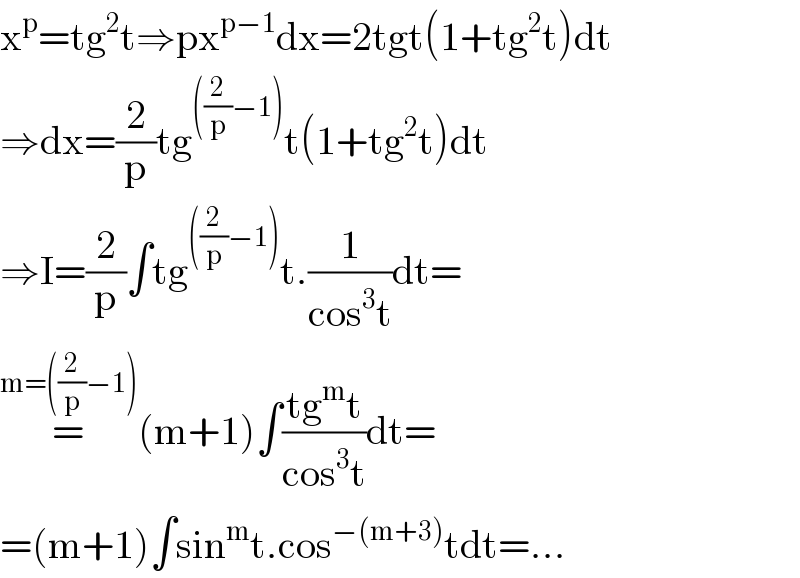
$$\mathrm{x}^{\mathrm{p}} =\mathrm{tg}^{\mathrm{2}} \mathrm{t}\Rightarrow\mathrm{px}^{\mathrm{p}−\mathrm{1}} \mathrm{dx}=\mathrm{2tgt}\left(\mathrm{1}+\mathrm{tg}^{\mathrm{2}} \mathrm{t}\right)\mathrm{dt} \\ $$$$\Rightarrow\mathrm{dx}=\frac{\mathrm{2}}{\mathrm{p}}\mathrm{tg}^{\left(\frac{\mathrm{2}}{\mathrm{p}}−\mathrm{1}\right)} \mathrm{t}\left(\mathrm{1}+\mathrm{tg}^{\mathrm{2}} \mathrm{t}\right)\mathrm{dt} \\ $$$$\Rightarrow\mathrm{I}=\frac{\mathrm{2}}{\mathrm{p}}\int\mathrm{tg}^{\left(\frac{\mathrm{2}}{\mathrm{p}}−\mathrm{1}\right)} \mathrm{t}.\frac{\mathrm{1}}{\mathrm{cos}^{\mathrm{3}} \mathrm{t}}\mathrm{dt}= \\ $$$$\overset{\mathrm{m}=\left(\frac{\mathrm{2}}{\mathrm{p}}−\mathrm{1}\right)} {=}\left(\mathrm{m}+\mathrm{1}\right)\int\frac{\mathrm{tg}^{\mathrm{m}} \mathrm{t}}{\mathrm{cos}^{\mathrm{3}} \mathrm{t}}\mathrm{dt}= \\ $$$$=\left(\mathrm{m}+\mathrm{1}\right)\int\mathrm{sin}^{\mathrm{m}} \mathrm{t}.\mathrm{cos}^{−\left(\mathrm{m}+\mathrm{3}\right)} \mathrm{tdt}=... \\ $$
Commented by mind is power last updated on 12/Feb/20
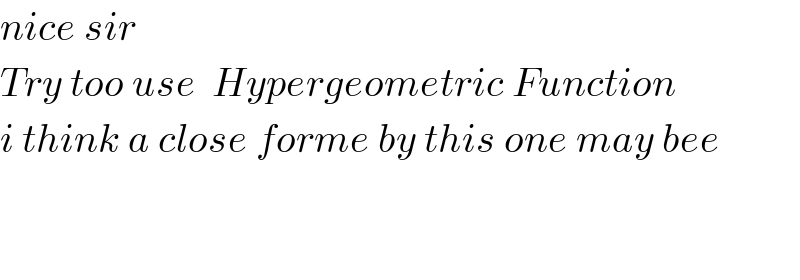
$${nice}\:{sir}\:\:\: \\ $$$${Try}\:{too}\:{use}\:\:{Hypergeometric}\:{Function}\: \\ $$$${i}\:{think}\:{a}\:{close}\:{forme}\:{by}\:{this}\:{one}\:{may}\:{bee} \\ $$$$ \\ $$$$ \\ $$
