
Question Number 80828 by jagoll last updated on 07/Feb/20
![given lim_(x→−∞) [(√(2x+p)) −(√(2x+1))]×(√(2x−p ))= (1/4)p find p .](Q80828.png)
$${given}\: \\ $$$$\underset{{x}\rightarrow−\infty} {\mathrm{lim}}\:\left[\sqrt{\mathrm{2}{x}+{p}}\:−\sqrt{\mathrm{2}{x}+\mathrm{1}}\right]×\sqrt{\mathrm{2}{x}−{p}\:}=\:\frac{\mathrm{1}}{\mathrm{4}}{p} \\ $$$${find}\:{p}\:. \\ $$
Commented by john santu last updated on 07/Feb/20
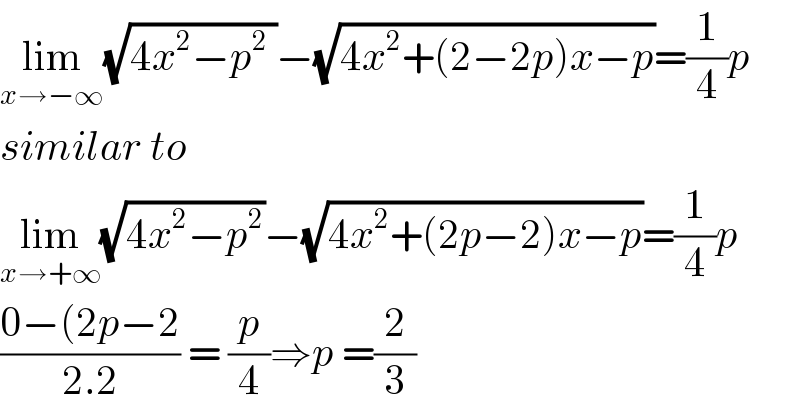
$$\underset{{x}\rightarrow−\infty} {\mathrm{lim}}\sqrt{\mathrm{4}{x}^{\mathrm{2}} −{p}^{\mathrm{2}} \:}−\sqrt{\mathrm{4}{x}^{\mathrm{2}} +\left(\mathrm{2}−\mathrm{2}{p}\right){x}−{p}}=\frac{\mathrm{1}}{\mathrm{4}}{p} \\ $$$${similar}\:{to} \\ $$$$\underset{{x}\rightarrow+\infty} {\mathrm{lim}}\sqrt{\mathrm{4}{x}^{\mathrm{2}} −{p}^{\mathrm{2}} }−\sqrt{\mathrm{4}{x}^{\mathrm{2}} +\left(\mathrm{2}{p}−\mathrm{2}\right){x}−{p}}=\frac{\mathrm{1}}{\mathrm{4}}{p} \\ $$$$\frac{\mathrm{0}−\left(\mathrm{2}{p}−\mathrm{2}\right.}{\mathrm{2}.\mathrm{2}}\:=\:\frac{{p}}{\mathrm{4}}\Rightarrow{p}\:=\frac{\mathrm{2}}{\mathrm{3}} \\ $$
Commented by jagoll last updated on 07/Feb/20

$${thx} \\ $$
