
Question Number 80748 by jagoll last updated on 06/Feb/20
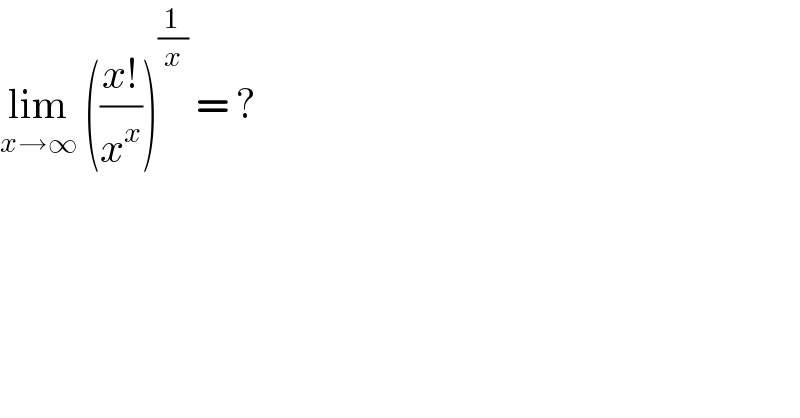
$$\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\left(\frac{{x}!}{{x}^{{x}} }\right)^{\frac{\mathrm{1}}{{x}}} \:=\:? \\ $$
Commented by john santu last updated on 06/Feb/20
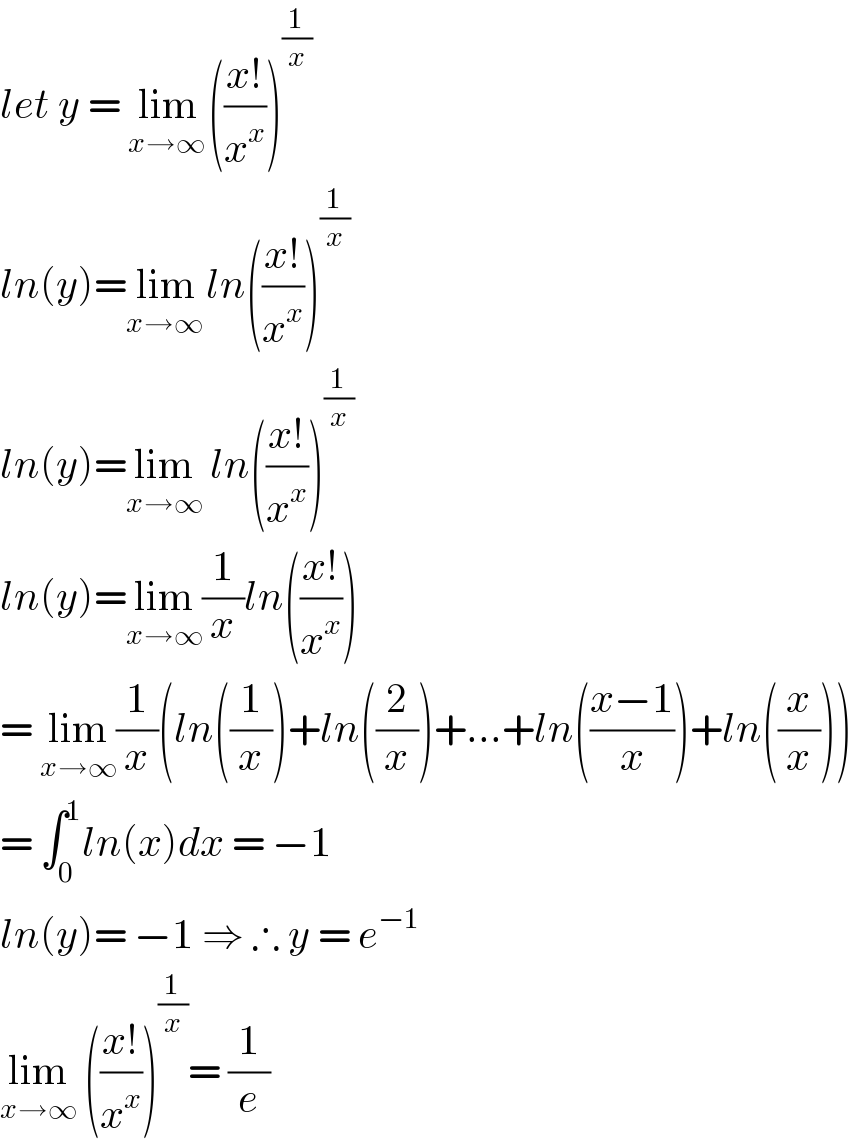
$${let}\:{y}\:=\:\underset{{x}\rightarrow\infty\:} {\mathrm{lim}}\left(\frac{{x}!}{{x}^{{x}} }\right)^{\frac{\mathrm{1}}{{x}}} \\ $$$${ln}\left({y}\right)=\underset{{x}\rightarrow\infty\:} {\mathrm{lim}}{ln}\left(\frac{{x}!}{{x}^{{x}} }\right)^{\frac{\mathrm{1}}{{x}}} \\ $$$${ln}\left({y}\right)=\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:{ln}\left(\frac{{x}!}{{x}^{{x}} }\right)^{\frac{\mathrm{1}}{{x}}} \\ $$$${ln}\left({y}\right)=\underset{{x}\rightarrow\infty} {\mathrm{lim}}\frac{\mathrm{1}}{{x}}{ln}\left(\frac{{x}!}{{x}^{{x}} }\right) \\ $$$$=\:\underset{{x}\rightarrow\infty} {\mathrm{lim}}\frac{\mathrm{1}}{{x}}\left({ln}\left(\frac{\mathrm{1}}{{x}}\right)+{ln}\left(\frac{\mathrm{2}}{{x}}\right)+...+{ln}\left(\frac{{x}−\mathrm{1}}{{x}}\right)+{ln}\left(\frac{{x}}{{x}}\right)\right) \\ $$$$=\:\int_{\mathrm{0}} ^{\mathrm{1}} {ln}\left({x}\right){dx}\:=\:−\mathrm{1} \\ $$$${ln}\left({y}\right)=\:−\mathrm{1}\:\Rightarrow\:\therefore\:{y}\:=\:{e}^{−\mathrm{1}} \\ $$$$\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\left(\frac{{x}!}{{x}^{{x}} }\right)^{\frac{\mathrm{1}}{{x}}} =\:\frac{\mathrm{1}}{{e}} \\ $$
Commented by jagoll last updated on 06/Feb/20

$${thanks} \\ $$
Commented by mathmax by abdo last updated on 06/Feb/20
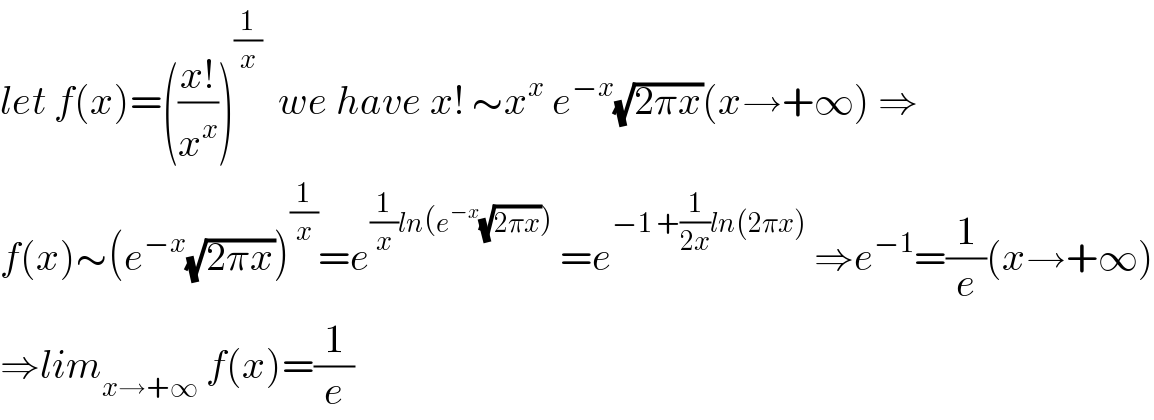
$${let}\:{f}\left({x}\right)=\left(\frac{{x}!}{{x}^{{x}} }\right)^{\frac{\mathrm{1}}{{x}}} \:\:{we}\:{have}\:{x}!\:\sim{x}^{{x}} \:{e}^{−{x}} \sqrt{\mathrm{2}\pi{x}}\left({x}\rightarrow+\infty\right)\:\Rightarrow \\ $$$${f}\left({x}\right)\sim\left({e}^{−{x}} \sqrt{\mathrm{2}\pi{x}}\right)^{\frac{\mathrm{1}}{{x}}} ={e}^{\frac{\mathrm{1}}{{x}}{ln}\left({e}^{−{x}} \sqrt{\mathrm{2}\pi{x}}\right)} \:={e}^{−\mathrm{1}\:+\frac{\mathrm{1}}{\mathrm{2}{x}}{ln}\left(\mathrm{2}\pi{x}\right)} \:\Rightarrow{e}^{−\mathrm{1}} =\frac{\mathrm{1}}{{e}}\left({x}\rightarrow+\infty\right) \\ $$$$\Rightarrow{lim}_{{x}\rightarrow+\infty} \:{f}\left({x}\right)=\frac{\mathrm{1}}{{e}} \\ $$
Answered by MJS last updated on 06/Feb/20
![lim_(x→∞) (((x!)/x^x ))^(1/x) = [x!≈(x^x /e^x )(√(2πx)) Sterling′s approximation] =(1/e)lim_(x→∞) (2πx)^(1/(2x)) =(1/e) [lim_(x→∞) C_1 ^(1/x) =1 ∀C_1 >0] [lim_(x→∞) x^(1/(C_2 x)) =lim_(x→∞) e^((ln x)/(C_2 x)) =10^0 =1 ∀C_2 ≠0]](Q80759.png)
$$\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\left(\frac{{x}!}{{x}^{{x}} }\right)^{\frac{\mathrm{1}}{{x}}} \:= \\ $$$$\:\:\:\:\:\left[{x}!\approx\frac{{x}^{{x}} }{\mathrm{e}^{{x}} }\sqrt{\mathrm{2}\pi{x}}\:\:\mathrm{Sterling}'\mathrm{s}\:\mathrm{approximation}\right] \\ $$$$=\frac{\mathrm{1}}{\mathrm{e}}\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\left(\mathrm{2}\pi{x}\right)^{\frac{\mathrm{1}}{\mathrm{2}{x}}} \:=\frac{\mathrm{1}}{\mathrm{e}} \\ $$$$\:\:\:\:\:\left[\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:{C}_{\mathrm{1}} ^{\frac{\mathrm{1}}{{x}}} =\mathrm{1}\:\forall{C}_{\mathrm{1}} >\mathrm{0}\right] \\ $$$$\:\:\:\:\:\left[\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:{x}^{\frac{\mathrm{1}}{{C}_{\mathrm{2}} {x}}} \:=\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\mathrm{e}^{\frac{\mathrm{ln}\:\:{x}}{{C}_{\mathrm{2}} {x}}} =\mathrm{10}^{\mathrm{0}} =\mathrm{1}\:\forall{C}_{\mathrm{2}} \neq\mathrm{0}\right] \\ $$
Commented by jagoll last updated on 06/Feb/20
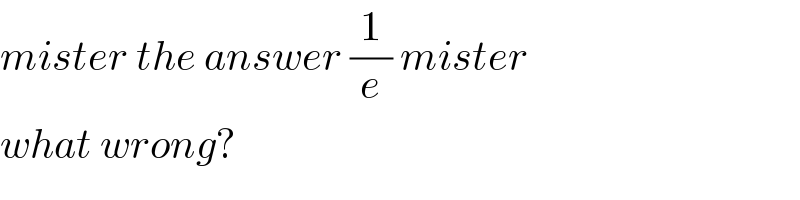
$${mister}\:{the}\:{answer}\:\frac{\mathrm{1}}{{e}}\:{mister} \\ $$$${what}\:{wrong}? \\ $$
Commented by MJS last updated on 06/Feb/20
$$\mathrm{the}\:\mathrm{answer}\:\mathrm{is}\:\mathrm{there}\:\mathrm{in}\:\mathrm{line}\:\mathrm{3} \\ $$
Commented by jagoll last updated on 06/Feb/20
$${oo}\:{thank}\:{you}\:{mister}.\:{i}\:{see}\:{the} \\ $$$${last}\:{line} \\ $$
