
Previous in Probability and Statistics Next in Probability and Statistics
Question Number 80746 by jagoll last updated on 06/Feb/20
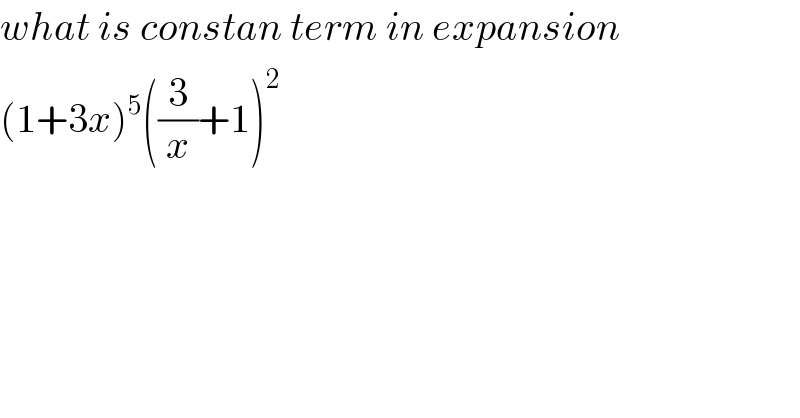
$${what}\:{is}\:{constan}\:{term}\:{in}\:{expansion} \\ $$$$\left(\mathrm{1}+\mathrm{3}{x}\right)^{\mathrm{5}} \left(\frac{\mathrm{3}}{{x}}+\mathrm{1}\right)^{\mathrm{2}} \\ $$
Commented by jagoll last updated on 06/Feb/20
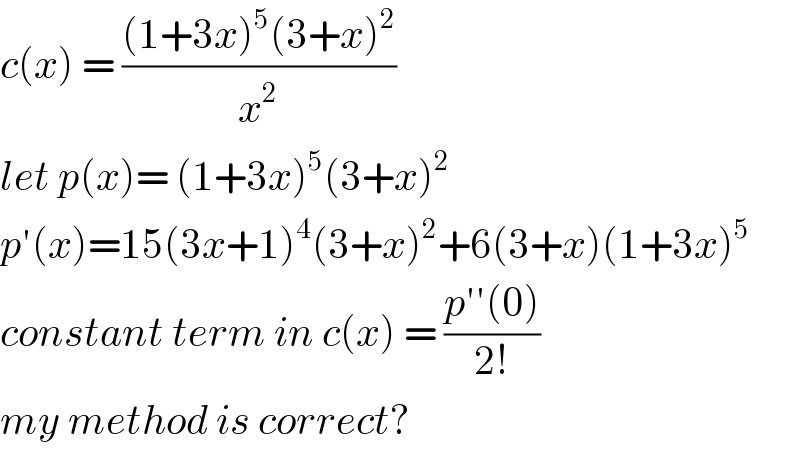
$${c}\left({x}\right)\:=\:\frac{\left(\mathrm{1}+\mathrm{3}{x}\right)^{\mathrm{5}} \left(\mathrm{3}+{x}\right)^{\mathrm{2}} }{{x}^{\mathrm{2}} } \\ $$$${let}\:{p}\left({x}\right)=\:\left(\mathrm{1}+\mathrm{3}{x}\right)^{\mathrm{5}} \left(\mathrm{3}+{x}\right)^{\mathrm{2}} \\ $$$${p}'\left({x}\right)=\mathrm{15}\left(\mathrm{3}{x}+\mathrm{1}\right)^{\mathrm{4}} \left(\mathrm{3}+{x}\right)^{\mathrm{2}} +\mathrm{6}\left(\mathrm{3}+{x}\right)\left(\mathrm{1}+\mathrm{3}{x}\right)^{\mathrm{5}} \\ $$$${constant}\:{term}\:{in}\:{c}\left({x}\right)\:=\:\frac{{p}''\left(\mathrm{0}\right)}{\mathrm{2}!} \\ $$$${my}\:{method}\:{is}\:{correct}? \\ $$
Commented by mathmax by abdo last updated on 06/Feb/20

$${we}\:{have}\:\left(\mathrm{3}{x}+\mathrm{1}\right)^{\mathrm{5}} \left(\frac{{x}+\mathrm{3}}{{x}}\right)^{\mathrm{2}} =\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\left(\mathrm{3}{x}+\mathrm{1}\right)^{\mathrm{5}} \left({x}^{\mathrm{2}} \:+\mathrm{6}{x}\:+\mathrm{9}\right) \\ $$$$=\left(\mathrm{3}{x}+\mathrm{1}\right)^{\mathrm{5}} \:+\frac{\mathrm{6}}{{x}}\left(\mathrm{3}{x}+\mathrm{1}\right)^{\mathrm{5}} \:+\frac{\mathrm{9}}{{x}^{\mathrm{2}} }\left(\mathrm{3}{x}+\mathrm{1}\right)^{\mathrm{5}} \\ $$$${the}\:{costant}\:{term}\:{in}\left(\mathrm{3}{x}+\mathrm{1}\right)^{\mathrm{5}} {is}\mathrm{1} \\ $$$$\frac{\mathrm{6}}{{x}}\left(\mathrm{3}{x}+\mathrm{1}\right)^{\mathrm{5}} =\frac{\mathrm{6}}{{x}}\sum_{{k}=\mathrm{0}} ^{\mathrm{5}} \:{C}_{\mathrm{5}} ^{{k}} \left(\mathrm{3}{x}\right)^{{k}} \:=\mathrm{6}\sum_{{k}=\mathrm{0}} ^{\mathrm{5}} \mathrm{3}^{{k}} \:{C}_{\mathrm{5}} ^{{k}} \:{x}^{{k}−\mathrm{1}} \\ $$$${term}\:{constant}\:\Rightarrow{k}=\mathrm{1}\:\Rightarrow{c}_{\mathrm{1}} =\mathrm{6}×\mathrm{3}^{\mathrm{1}} ×{C}_{\mathrm{5}} ^{\mathrm{1}} \:=\mathrm{18}×\mathrm{5}\:=\mathrm{90} \\ $$$$\frac{\mathrm{9}}{{x}^{\mathrm{2}} }\left(\mathrm{3}{x}+\mathrm{1}\right)^{\mathrm{5}} \:=\frac{\mathrm{9}}{{x}^{\mathrm{2}} }\sum_{{k}=\mathrm{0}} ^{\mathrm{5}} \:{C}_{\mathrm{5}} ^{{k}} \left(\mathrm{3}{x}\right)^{{k}} \:=\mathrm{9}\sum_{{k}=\mathrm{0}} ^{\mathrm{5}} \:\mathrm{3}^{{k}} \:{C}_{\mathrm{5}} ^{{k}} \:{x}^{{k}−\mathrm{2}} \\ $$$${term}\:{constant}\:\Rightarrow{k}=\mathrm{2}\:\Rightarrow{c}_{\mathrm{2}} =\mathrm{9}×\mathrm{3}^{\mathrm{2}} ×{C}_{\mathrm{5}} ^{\mathrm{2}} \:=\mathrm{81}×\frac{\mathrm{5}!}{\mathrm{2}!\mathrm{3}!} \\ $$$$=\mathrm{81}×\frac{\mathrm{5}×\mathrm{4}}{\mathrm{2}}\:=\mathrm{810}\:\Rightarrow\:{the}\:{constant}\:{term}\:{in}\:\left(\mathrm{1}+\mathrm{3}{x}\right)^{\mathrm{5}} \left(\frac{\mathrm{3}}{{x}}+\mathrm{1}\right)^{\mathrm{2}} \\ $$$${is}\mathrm{1}+\mathrm{90}+\mathrm{810}\:=\mathrm{901} \\ $$
Answered by ajfour last updated on 06/Feb/20
![E=(1/x^2 )(1+3x)^5 (3+x)^2 constant term in E is same as coefficient of x^2 in x^2 E = 1+[2×3×5(3)]+[9×10×9] = 1+90+810 = 901 .](Q80749.png)
$${E}=\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\left(\mathrm{1}+\mathrm{3}{x}\right)^{\mathrm{5}} \left(\mathrm{3}+{x}\right)^{\mathrm{2}} \\ $$$$\:\:{constant}\:{term}\:{in}\:{E}\:{is}\:{same}\:{as} \\ $$$${coefficient}\:{of}\:{x}^{\mathrm{2}} \:{in}\:{x}^{\mathrm{2}} {E} \\ $$$$\:\:\:=\:\mathrm{1}+\left[\mathrm{2}×\mathrm{3}×\mathrm{5}\left(\mathrm{3}\right)\right]+\left[\mathrm{9}×\mathrm{10}×\mathrm{9}\right] \\ $$$$\:\:\:=\:\mathrm{1}+\mathrm{90}+\mathrm{810}\:=\:\mathrm{901}\:. \\ $$
Commented by john santu last updated on 06/Feb/20
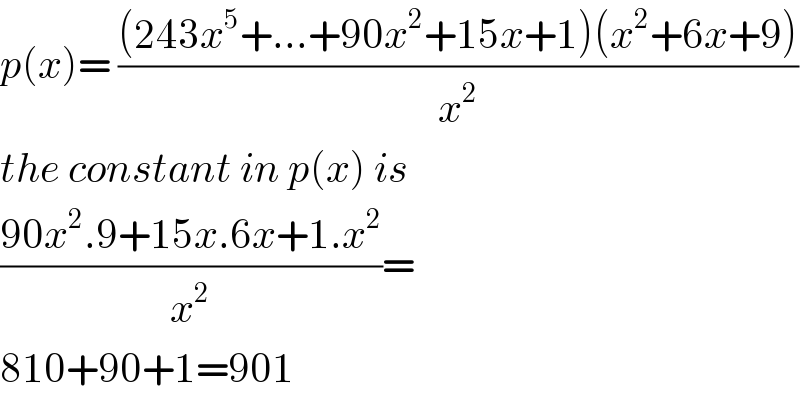
$${p}\left({x}\right)=\:\frac{\left(\mathrm{243}{x}^{\mathrm{5}} +...+\mathrm{90}{x}^{\mathrm{2}} +\mathrm{15}{x}+\mathrm{1}\right)\left({x}^{\mathrm{2}} +\mathrm{6}{x}+\mathrm{9}\right)}{{x}^{\mathrm{2}} } \\ $$$${the}\:{constant}\:{in}\:{p}\left({x}\right)\:{is}\: \\ $$$$\frac{\mathrm{90}{x}^{\mathrm{2}} .\mathrm{9}+\mathrm{15}{x}.\mathrm{6}{x}+\mathrm{1}.{x}^{\mathrm{2}} }{{x}^{\mathrm{2}} }= \\ $$$$\mathrm{810}+\mathrm{90}+\mathrm{1}=\mathrm{901} \\ $$
