
Question Number 80543 by Power last updated on 04/Feb/20
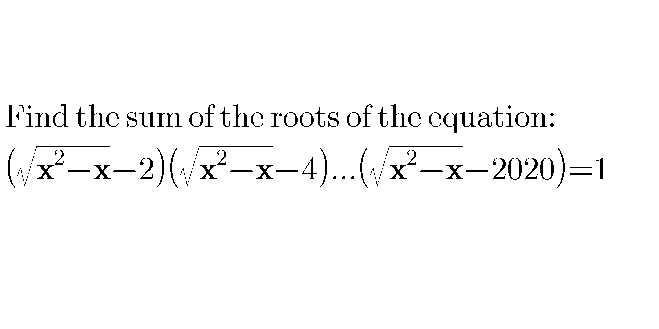
Commented by mr W last updated on 04/Feb/20

$$\mathrm{1010} \\ $$
Commented by Power last updated on 04/Feb/20

$$\mathrm{solution}\:\mathrm{sir} \\ $$
Commented by jagoll last updated on 04/Feb/20
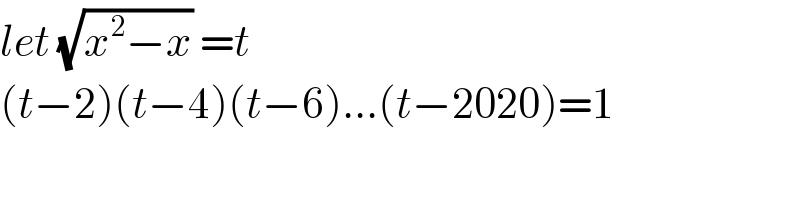
$${let}\:\sqrt{{x}^{\mathrm{2}} −{x}}\:={t} \\ $$$$\left({t}−\mathrm{2}\right)\left({t}−\mathrm{4}\right)\left({t}−\mathrm{6}\right)...\left({t}−\mathrm{2020}\right)=\mathrm{1} \\ $$
Commented by jagoll last updated on 04/Feb/20
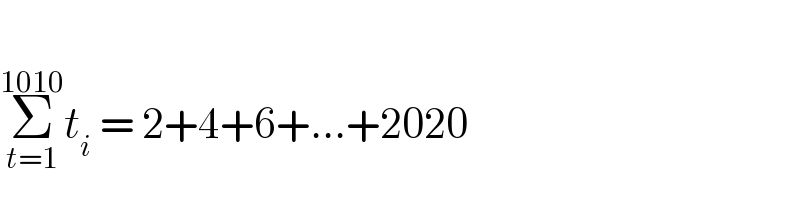
$$ \\ $$$$\underset{{t}=\mathrm{1}} {\overset{\mathrm{1010}} {\sum}}{t}_{{i}} \:=\:\mathrm{2}+\mathrm{4}+\mathrm{6}+...+\mathrm{2020} \\ $$
Commented by mr W last updated on 04/Feb/20
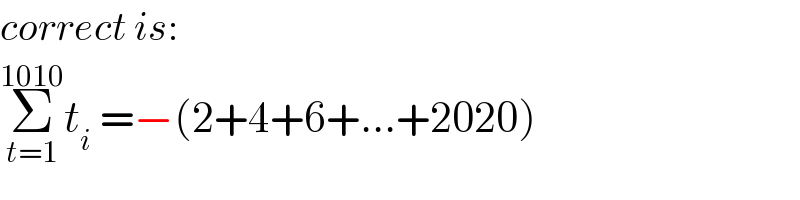
$${correct}\:{is}: \\ $$$$\underset{{t}=\mathrm{1}} {\overset{\mathrm{1010}} {\sum}}{t}_{{i}} \:=−\left(\mathrm{2}+\mathrm{4}+\mathrm{6}+...+\mathrm{2020}\right) \\ $$
Commented by jagoll last updated on 04/Feb/20
$${oo}\:{yes}\:{sir}.\:{thank}\:{you} \\ $$
Answered by mr W last updated on 04/Feb/20
![let (√(x^2 −x))=2z (2z−2)(2z−4)...(2z−2020)=1 2^(1010) (z−1)(z−2)...(z−1010)=1 (z−1)(z−2)...(z−1010)−(1/2^(1010) )=0 this eqn. has 1010 roots for z, say z_1 ,z_2 ,...,z_(1010) Σ_(i=1) ^(1010) z_i =−(1+2+...+1010)=−510555 Π_(i=1) ^(1010) z_i =1×2×...×1010−(1/2^(1010) )=1010!−(1/2^(1010) ) (√(x^2 −x))=2z_i (i=1,2,...,1010) x^2 −x−4z_i ^2 =0 for each z_i there are two roots for x: x_(i,1) and x_(i,2) with x_(i,1) +x_(i,2) =1, x_(i,1) x_(i,2) =−4z_i ^2 sum of all roots for x: Σx=Σ_(i=1) ^(1010) (x_(i,1) +x_(i,2) )=Σ_(i=1) ^(1010) 1=1010 product of all roots for x: Πx=Π_(i=1) ^(1010) (x_(i,1) x_(i,2) )=Π_(i=1) ^(1010) (−4z_i ^2 ) =(−4)^(1010) [Π_(i=1) ^(1010) z_i ]^2 =2^(2020) [1010!−(1/2^(1010) )]^2 =(2^(1010) ×1010!−1)^2 ⇒sum of all roots =1010 ⇒answer ⇒product of all roots =(2^(1010) ×1010!−1)^2](Q80578.png)
$${let}\:\sqrt{{x}^{\mathrm{2}} −{x}}=\mathrm{2}{z} \\ $$$$\left(\mathrm{2}{z}−\mathrm{2}\right)\left(\mathrm{2}{z}−\mathrm{4}\right)...\left(\mathrm{2}{z}−\mathrm{2020}\right)=\mathrm{1} \\ $$$$\mathrm{2}^{\mathrm{1010}} \left({z}−\mathrm{1}\right)\left({z}−\mathrm{2}\right)...\left({z}−\mathrm{1010}\right)=\mathrm{1} \\ $$$$\left({z}−\mathrm{1}\right)\left({z}−\mathrm{2}\right)...\left({z}−\mathrm{1010}\right)−\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{1010}} }=\mathrm{0} \\ $$$${this}\:{eqn}.\:{has}\:\mathrm{1010}\:{roots}\:{for}\:{z},\:{say} \\ $$$${z}_{\mathrm{1}} ,{z}_{\mathrm{2}} ,...,{z}_{\mathrm{1010}} \\ $$$$\underset{{i}=\mathrm{1}} {\overset{\mathrm{1010}} {\sum}}{z}_{{i}} =−\left(\mathrm{1}+\mathrm{2}+...+\mathrm{1010}\right)=−\mathrm{510555} \\ $$$$\underset{{i}=\mathrm{1}} {\overset{\mathrm{1010}} {\prod}}{z}_{{i}} =\mathrm{1}×\mathrm{2}×...×\mathrm{1010}−\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{1010}} }=\mathrm{1010}!−\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{1010}} } \\ $$$$ \\ $$$$\sqrt{{x}^{\mathrm{2}} −{x}}=\mathrm{2}{z}_{{i}} \:\:\left({i}=\mathrm{1},\mathrm{2},...,\mathrm{1010}\right) \\ $$$${x}^{\mathrm{2}} −{x}−\mathrm{4}{z}_{{i}} ^{\mathrm{2}} =\mathrm{0} \\ $$$${for}\:{each}\:{z}_{{i}} \:{there}\:{are}\:{two}\:{roots}\:{for}\:{x}: \\ $$$${x}_{{i},\mathrm{1}} \:{and}\:{x}_{{i},\mathrm{2}} \:{with} \\ $$$${x}_{{i},\mathrm{1}} +{x}_{{i},\mathrm{2}} =\mathrm{1},\:{x}_{{i},\mathrm{1}} {x}_{{i},\mathrm{2}} =−\mathrm{4}{z}_{{i}} ^{\mathrm{2}} \\ $$$$ \\ $$$${sum}\:{of}\:{all}\:{roots}\:{for}\:{x}: \\ $$$$\Sigma{x}=\underset{{i}=\mathrm{1}} {\overset{\mathrm{1010}} {\sum}}\left({x}_{{i},\mathrm{1}} +{x}_{{i},\mathrm{2}} \right)=\underset{{i}=\mathrm{1}} {\overset{\mathrm{1010}} {\sum}}\mathrm{1}=\mathrm{1010} \\ $$$$ \\ $$$${product}\:{of}\:{all}\:{roots}\:{for}\:{x}: \\ $$$$\Pi{x}=\underset{{i}=\mathrm{1}} {\overset{\mathrm{1010}} {\prod}}\left({x}_{{i},\mathrm{1}} {x}_{{i},\mathrm{2}} \right)=\underset{{i}=\mathrm{1}} {\overset{\mathrm{1010}} {\prod}}\left(−\mathrm{4}{z}_{{i}} ^{\mathrm{2}} \right) \\ $$$$=\left(−\mathrm{4}\right)^{\mathrm{1010}} \left[\underset{{i}=\mathrm{1}} {\overset{\mathrm{1010}} {\prod}}{z}_{{i}} \right]^{\mathrm{2}} \\ $$$$=\mathrm{2}^{\mathrm{2020}} \left[\mathrm{1010}!−\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{1010}} }\right]^{\mathrm{2}} \\ $$$$=\left(\mathrm{2}^{\mathrm{1010}} ×\mathrm{1010}!−\mathrm{1}\right)^{\mathrm{2}} \\ $$$$ \\ $$$$\Rightarrow{sum}\:{of}\:{all}\:{roots}\:=\mathrm{1010}\:\Rightarrow\boldsymbol{{answer}} \\ $$$$\Rightarrow{product}\:{of}\:{all}\:{roots}\:=\left(\mathrm{2}^{\mathrm{1010}} ×\mathrm{1010}!−\mathrm{1}\right)^{\mathrm{2}} \\ $$
Commented by Power last updated on 04/Feb/20

$$\mathrm{thanks} \\ $$
