
Question Number 79190 by mr W last updated on 23/Jan/20
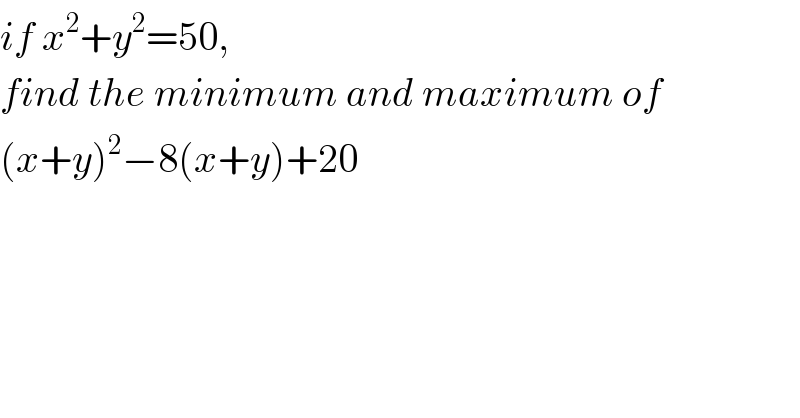
$${if}\:{x}^{\mathrm{2}} +{y}^{\mathrm{2}} =\mathrm{50}, \\ $$$${find}\:{the}\:{minimum}\:{and}\:{maximum}\:{of} \\ $$$$\left({x}+{y}\right)^{\mathrm{2}} −\mathrm{8}\left({x}+{y}\right)+\mathrm{20} \\ $$
Commented by jagoll last updated on 23/Jan/20
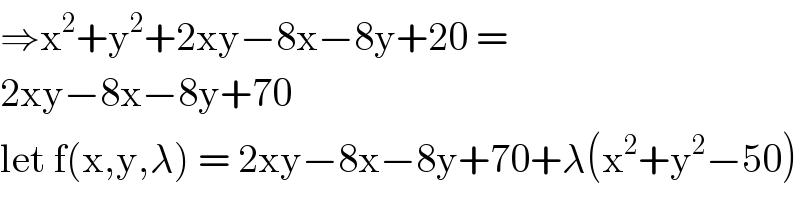
$$\Rightarrow\mathrm{x}^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} +\mathrm{2xy}−\mathrm{8x}−\mathrm{8y}+\mathrm{20}\:= \\ $$$$\mathrm{2xy}−\mathrm{8x}−\mathrm{8y}+\mathrm{70} \\ $$$$\mathrm{let}\:\mathrm{f}\left(\mathrm{x},\mathrm{y},\lambda\right)\:=\:\mathrm{2xy}−\mathrm{8x}−\mathrm{8y}+\mathrm{70}+\lambda\left(\mathrm{x}^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} −\mathrm{50}\right) \\ $$
Commented by jagoll last updated on 23/Jan/20
$$\mathrm{we}\:\mathrm{use}\:\mathrm{differential} \\ $$
Commented by jagoll last updated on 23/Jan/20

$$\mathrm{right}\:\mathrm{sir}? \\ $$
Commented by jagoll last updated on 23/Jan/20
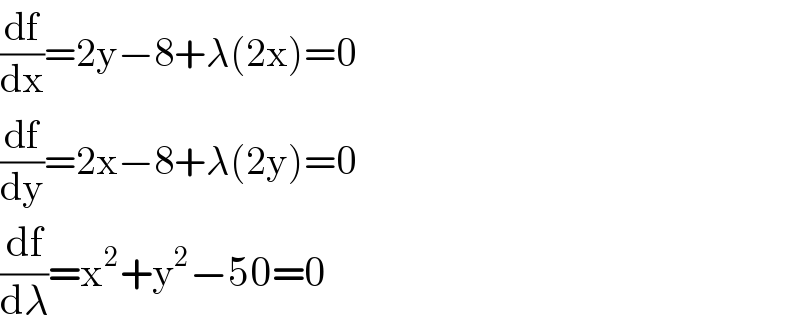
$$\frac{\mathrm{df}}{\mathrm{dx}}=\mathrm{2y}−\mathrm{8}+\lambda\left(\mathrm{2x}\right)=\mathrm{0} \\ $$$$\frac{\mathrm{df}}{\mathrm{dy}}=\mathrm{2x}−\mathrm{8}+\lambda\left(\mathrm{2y}\right)=\mathrm{0} \\ $$$$\frac{\mathrm{df}}{\mathrm{d}\lambda}=\mathrm{x}^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} −\mathrm{50}=\mathrm{0} \\ $$
Commented by mind is power last updated on 23/Jan/20
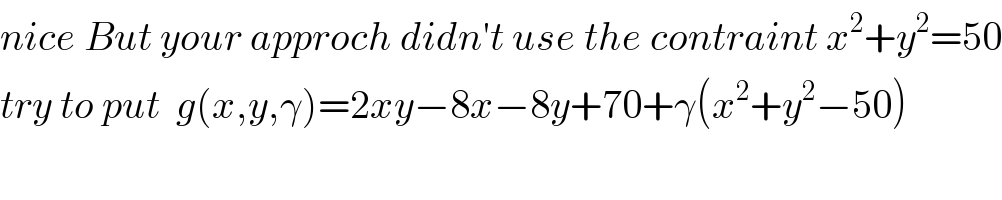
$${nice}\:{But}\:{your}\:{approch}\:{didn}'{t}\:{use}\:{the}\:{contraint}\:{x}^{\mathrm{2}} +{y}^{\mathrm{2}} =\mathrm{50} \\ $$$${try}\:{to}\:{put}\:\:{g}\left({x},{y},\gamma\right)=\mathrm{2}{xy}−\mathrm{8}{x}−\mathrm{8}{y}+\mathrm{70}+\gamma\left({x}^{\mathrm{2}} +{y}^{\mathrm{2}} −\mathrm{50}\right) \\ $$$$ \\ $$
Commented by jagoll last updated on 23/Jan/20
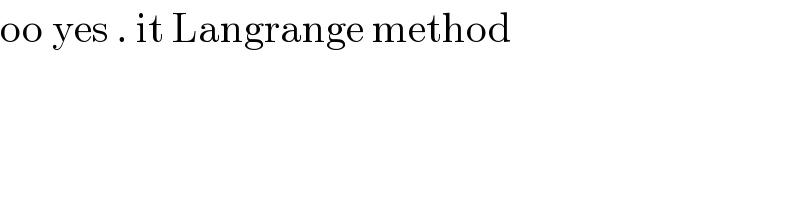
$$\mathrm{oo}\:\mathrm{yes}\:.\:\mathrm{it}\:\mathrm{Langrange}\:\mathrm{method} \\ $$
Commented by jagoll last updated on 23/Jan/20

$$\mathrm{thank}\:\mathrm{you}\:\mathrm{sir} \\ $$
Commented by jagoll last updated on 23/Jan/20

$$\mathrm{that}\:\mathrm{right}\:\mathrm{sir}? \\ $$
Commented by jagoll last updated on 23/Jan/20
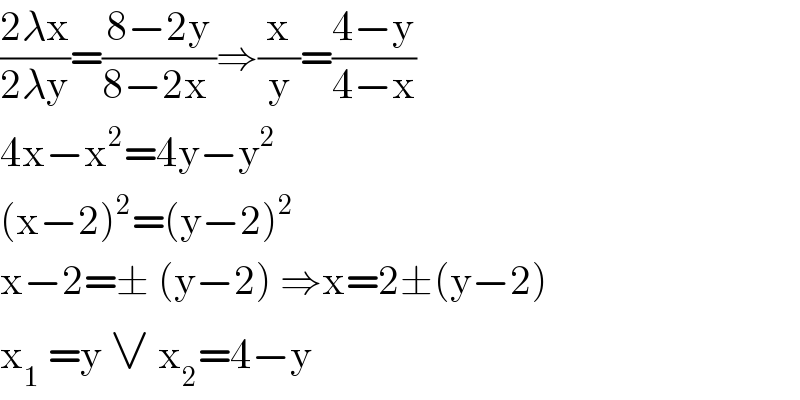
$$\frac{\mathrm{2}\lambda\mathrm{x}}{\mathrm{2}\lambda\mathrm{y}}=\frac{\mathrm{8}−\mathrm{2y}}{\mathrm{8}−\mathrm{2x}\:}\Rightarrow\frac{\mathrm{x}}{\mathrm{y}}=\frac{\mathrm{4}−\mathrm{y}}{\mathrm{4}−\mathrm{x}} \\ $$$$\mathrm{4x}−\mathrm{x}^{\mathrm{2}} =\mathrm{4y}−\mathrm{y}^{\mathrm{2}} \\ $$$$\left(\mathrm{x}−\mathrm{2}\right)^{\mathrm{2}} =\left(\mathrm{y}−\mathrm{2}\right)^{\mathrm{2}} \\ $$$$\mathrm{x}−\mathrm{2}=\pm\:\left(\mathrm{y}−\mathrm{2}\right)\:\Rightarrow\mathrm{x}=\mathrm{2}\pm\left(\mathrm{y}−\mathrm{2}\right) \\ $$$$\mathrm{x}_{\mathrm{1}} \:=\mathrm{y}\:\vee\:\mathrm{x}_{\mathrm{2}} =\mathrm{4}−\mathrm{y} \\ $$
Commented by jagoll last updated on 23/Jan/20
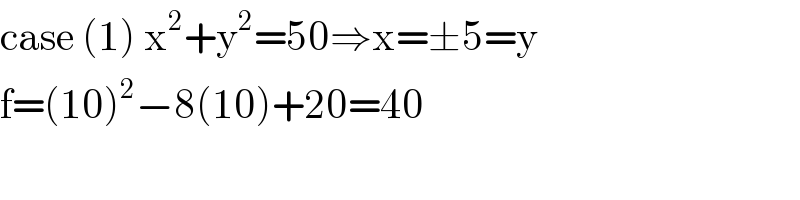
$$\mathrm{case}\:\left(\mathrm{1}\right)\:\mathrm{x}^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} =\mathrm{50}\Rightarrow\mathrm{x}=\pm\mathrm{5}=\mathrm{y} \\ $$$$\mathrm{f}=\left(\mathrm{10}\right)^{\mathrm{2}} −\mathrm{8}\left(\mathrm{10}\right)+\mathrm{20}=\mathrm{40} \\ $$
Commented by jagoll last updated on 23/Jan/20
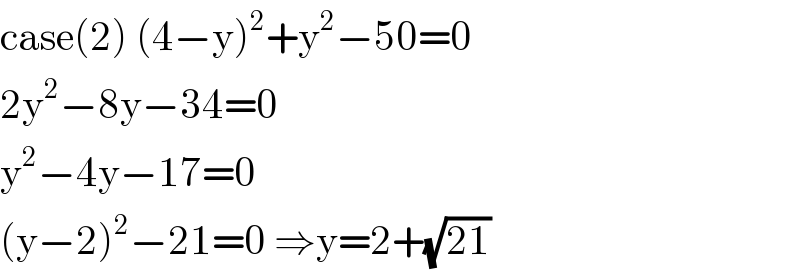
$$\mathrm{case}\left(\mathrm{2}\right)\:\left(\mathrm{4}−\mathrm{y}\right)^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} −\mathrm{50}=\mathrm{0} \\ $$$$\mathrm{2y}^{\mathrm{2}} −\mathrm{8y}−\mathrm{34}=\mathrm{0} \\ $$$$\mathrm{y}^{\mathrm{2}} −\mathrm{4y}−\mathrm{17}=\mathrm{0} \\ $$$$\left(\mathrm{y}−\mathrm{2}\right)^{\mathrm{2}} −\mathrm{21}=\mathrm{0}\:\Rightarrow\mathrm{y}=\mathrm{2}+\sqrt{\mathrm{21}} \\ $$
Commented by jagoll last updated on 23/Jan/20
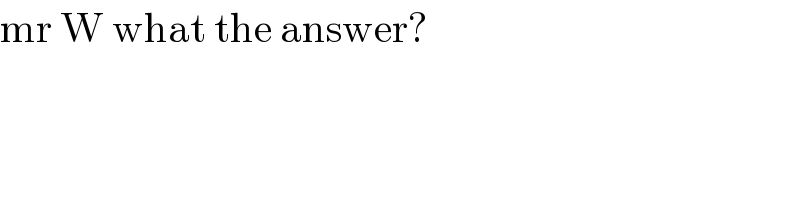
$$\mathrm{mr}\:\mathrm{W}\:\mathrm{what}\:\mathrm{the}\:\mathrm{answer}? \\ $$
Commented by mind is power last updated on 23/Jan/20

$${Nice}\:{Sir} \\ $$
Answered by mind is power last updated on 23/Jan/20
![x=(√(50))cos(θ) y=(√(50))sin(θ) x+y=(√(50)).(cos(θ)+sin(θ)) =10sin(θ+(π/4))=10sin(ϕ),ϕ∈[0,2π[ x+y∈[−10,10] (x+y)^2 −8(x+y)+20=f(x+y) f(t)=t^2 −8t+20 t∈[−10,10] f′(t)=2t−8,minf=f(4)=16−32+20=4 x+y=4=10sin(ϕ),ϕ=sin^(−1) ((2/5)),θ=sin^(−1) ((2/5))−(π/4) x=(√(50))cos(θ),y=(√(50))sin(θ) mox f(−10)=100+80+20=200 −10=10sin(ϕ)⇒ϕ=−(π/2)⇒θ=−((3π)/4) x=(√(50)).−((√2)/2)=−5 ,y=−5](Q79218.png)
$${x}=\sqrt{\mathrm{50}}{cos}\left(\theta\right) \\ $$$${y}=\sqrt{\mathrm{50}}{sin}\left(\theta\right) \\ $$$${x}+{y}=\sqrt{\mathrm{50}}.\left({cos}\left(\theta\right)+{sin}\left(\theta\right)\right) \\ $$$$=\mathrm{10}{sin}\left(\theta+\frac{\pi}{\mathrm{4}}\right)=\mathrm{10}{sin}\left(\varphi\right),\varphi\in\left[\mathrm{0},\mathrm{2}\pi\left[\right.\right. \\ $$$${x}+{y}\in\left[−\mathrm{10},\mathrm{10}\right] \\ $$$$\left({x}+{y}\right)^{\mathrm{2}} −\mathrm{8}\left({x}+{y}\right)+\mathrm{20}={f}\left({x}+{y}\right) \\ $$$${f}\left({t}\right)={t}^{\mathrm{2}} −\mathrm{8}{t}+\mathrm{20} \\ $$$${t}\in\left[−\mathrm{10},\mathrm{10}\right] \\ $$$${f}'\left({t}\right)=\mathrm{2}{t}−\mathrm{8},{minf}={f}\left(\mathrm{4}\right)=\mathrm{16}−\mathrm{32}+\mathrm{20}=\mathrm{4} \\ $$$${x}+{y}=\mathrm{4}=\mathrm{10}{sin}\left(\varphi\right),\varphi=\mathrm{sin}^{−\mathrm{1}} \left(\frac{\mathrm{2}}{\mathrm{5}}\right),\theta=\mathrm{sin}^{−\mathrm{1}} \left(\frac{\mathrm{2}}{\mathrm{5}}\right)−\frac{\pi}{\mathrm{4}} \\ $$$${x}=\sqrt{\mathrm{50}}{cos}\left(\theta\right),{y}=\sqrt{\mathrm{50}}{sin}\left(\theta\right) \\ $$$${mox}\:{f}\left(−\mathrm{10}\right)=\mathrm{100}+\mathrm{80}+\mathrm{20}=\mathrm{200} \\ $$$$−\mathrm{10}=\mathrm{10}{sin}\left(\varphi\right)\Rightarrow\varphi=−\frac{\pi}{\mathrm{2}}\Rightarrow\theta=−\frac{\mathrm{3}\pi}{\mathrm{4}} \\ $$$${x}=\sqrt{\mathrm{50}}.−\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}=−\mathrm{5}\:\:,{y}=−\mathrm{5} \\ $$$$ \\ $$
Answered by mr W last updated on 23/Jan/20
![it is to find the minimum and maximum of f=(x+y)^2 −8(x+y)+20 under the condition that x, y satisfy x^2 +y^2 =50, i.e. (x, y) is on the circle. let x=5(√2) cos θ, y=5(√2) sin θ f=(x+y)^2 −8(x+y)+20 =(x+y−4)^2 +4 =(5(√2) cos θ+5(√2) sin θ−4)^2 +4 =[10((1/(√2)) cos θ+(1/(√2)) sin θ)−4]^2 +4 =[10 cos (θ−(π/4))−4]^2 +4≥4 f_(min) is when cos (θ−(π/4))=(4/(10)), i.e. θ=(π/4)+cos^(−1) (2/5), f_(min) =(4−4)^2 +4=4 f_(max) is when cos (θ−(π/4))=−1, i.e. θ=((5π)/4), f_(max) =(−10−4)^2 +4=200](Q79224.png)
$${it}\:{is}\:{to}\:{find}\:{the}\:{minimum}\:{and}\: \\ $$$${maximum}\:{of}\:{f}=\left({x}+{y}\right)^{\mathrm{2}} −\mathrm{8}\left({x}+{y}\right)+\mathrm{20} \\ $$$${under}\:{the}\:{condition}\:{that}\:{x},\:{y}\:{satisfy} \\ $$$${x}^{\mathrm{2}} +{y}^{\mathrm{2}} =\mathrm{50},\:{i}.{e}.\:\left({x},\:{y}\right)\:{is}\:{on}\:{the}\:{circle}. \\ $$$${let}\:{x}=\mathrm{5}\sqrt{\mathrm{2}}\:\mathrm{cos}\:\theta,\:{y}=\mathrm{5}\sqrt{\mathrm{2}}\:\mathrm{sin}\:\theta \\ $$$${f}=\left({x}+{y}\right)^{\mathrm{2}} −\mathrm{8}\left({x}+{y}\right)+\mathrm{20} \\ $$$$=\left({x}+{y}−\mathrm{4}\right)^{\mathrm{2}} +\mathrm{4} \\ $$$$=\left(\mathrm{5}\sqrt{\mathrm{2}}\:\mathrm{cos}\:\theta+\mathrm{5}\sqrt{\mathrm{2}}\:\mathrm{sin}\:\theta−\mathrm{4}\right)^{\mathrm{2}} +\mathrm{4} \\ $$$$=\left[\mathrm{10}\left(\frac{\mathrm{1}}{\sqrt{\mathrm{2}}}\:\mathrm{cos}\:\theta+\frac{\mathrm{1}}{\sqrt{\mathrm{2}}}\:\mathrm{sin}\:\theta\right)−\mathrm{4}\right]^{\mathrm{2}} +\mathrm{4} \\ $$$$=\left[\mathrm{10}\:\mathrm{cos}\:\left(\theta−\frac{\pi}{\mathrm{4}}\right)−\mathrm{4}\right]^{\mathrm{2}} +\mathrm{4}\geqslant\mathrm{4} \\ $$$${f}_{{min}} \:{is}\:{when}\:\mathrm{cos}\:\left(\theta−\frac{\pi}{\mathrm{4}}\right)=\frac{\mathrm{4}}{\mathrm{10}},\:{i}.{e}.\:\theta=\frac{\pi}{\mathrm{4}}+\mathrm{cos}^{−\mathrm{1}} \frac{\mathrm{2}}{\mathrm{5}}, \\ $$$${f}_{{min}} =\left(\mathrm{4}−\mathrm{4}\right)^{\mathrm{2}} +\mathrm{4}=\mathrm{4} \\ $$$${f}_{{max}} \:{is}\:{when}\:\mathrm{cos}\:\left(\theta−\frac{\pi}{\mathrm{4}}\right)=−\mathrm{1},\:{i}.{e}.\:\theta=\frac{\mathrm{5}\pi}{\mathrm{4}}, \\ $$$${f}_{{max}} =\left(−\mathrm{10}−\mathrm{4}\right)^{\mathrm{2}} +\mathrm{4}=\mathrm{200} \\ $$
Answered by key of knowledge last updated on 23/Jan/20
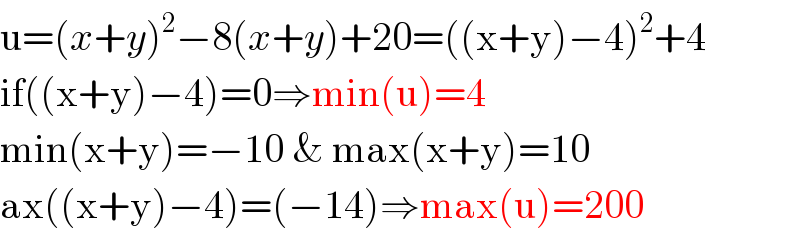
$$\mathrm{u}=\left({x}+{y}\right)^{\mathrm{2}} −\mathrm{8}\left({x}+{y}\right)+\mathrm{20}=\left(\left(\mathrm{x}+\mathrm{y}\right)−\mathrm{4}\right)^{\mathrm{2}} +\mathrm{4} \\ $$$$\mathrm{if}\left(\left(\mathrm{x}+\mathrm{y}\right)−\mathrm{4}\right)=\mathrm{0}\Rightarrow\mathrm{min}\left(\mathrm{u}\right)=\mathrm{4} \\ $$$$\mathrm{min}\left(\mathrm{x}+\mathrm{y}\right)=−\mathrm{10}\:\&\:\mathrm{max}\left(\mathrm{x}+\mathrm{y}\right)=\mathrm{10} \\ $$$$\mathrm{ax}\left(\left(\mathrm{x}+\mathrm{y}\right)−\mathrm{4}\right)=\left(−\mathrm{14}\right)\Rightarrow\mathrm{max}\left(\mathrm{u}\right)=\mathrm{200} \\ $$
Answered by john santu last updated on 24/Jan/20
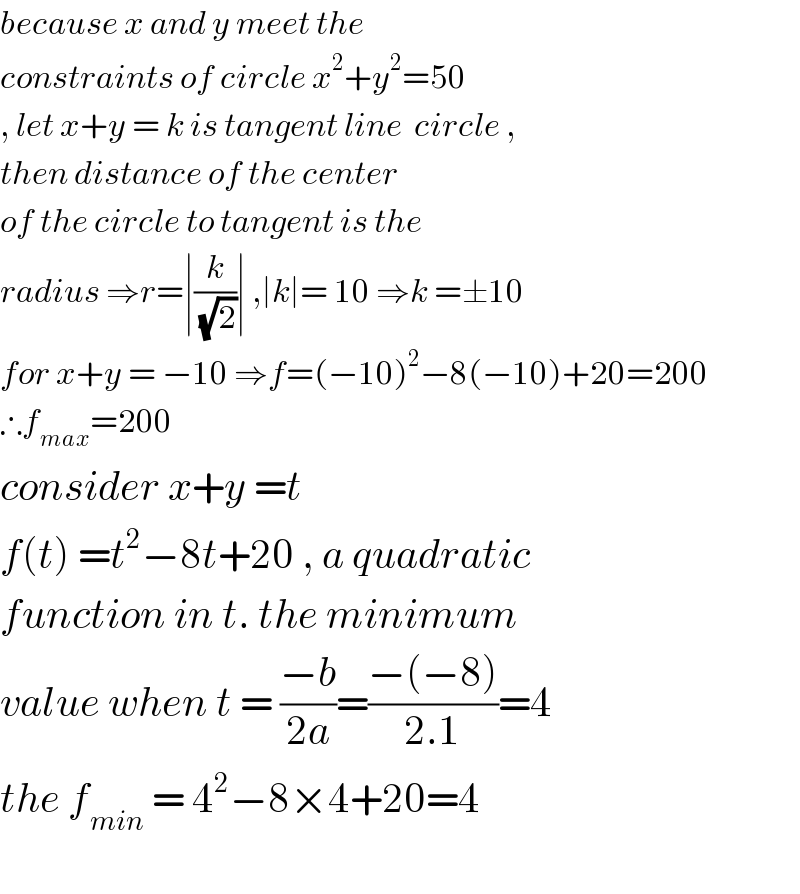
$${because}\:{x}\:{and}\:{y}\:{meet}\:{the}\: \\ $$$${constraints}\:{of}\:{circle}\:{x}^{\mathrm{2}} +{y}^{\mathrm{2}} =\mathrm{50} \\ $$$$,\:{let}\:{x}+{y}\:=\:{k}\:{is}\:{tangent}\:{line}\:\:{circle}\:, \\ $$$${then}\:{distance}\:{of}\:{the}\:{center}\: \\ $$$${of}\:{the}\:{circle}\:{to}\:{tangent}\:{is}\:{the} \\ $$$${radius}\:\Rightarrow{r}=\mid\frac{{k}}{\sqrt{\mathrm{2}}}\mid\:,\mid{k}\mid=\:\mathrm{10}\:\Rightarrow{k}\:=\pm\mathrm{10} \\ $$$${for}\:{x}+{y}\:=\:−\mathrm{10}\:\Rightarrow{f}=\left(−\mathrm{10}\right)^{\mathrm{2}} −\mathrm{8}\left(−\mathrm{10}\right)+\mathrm{20}=\mathrm{200} \\ $$$$\therefore{f}_{{max}} =\mathrm{200}\: \\ $$$${consider}\:{x}+{y}\:={t} \\ $$$${f}\left({t}\right)\:={t}^{\mathrm{2}} −\mathrm{8}{t}+\mathrm{20}\:,\:{a}\:{quadratic} \\ $$$${function}\:{in}\:{t}.\:{the}\:{minimum} \\ $$$${value}\:{when}\:{t}\:=\:\frac{−{b}}{\mathrm{2}{a}}=\frac{−\left(−\mathrm{8}\right)}{\mathrm{2}.\mathrm{1}}=\mathrm{4} \\ $$$${the}\:{f}_{{min}} \:=\:\mathrm{4}^{\mathrm{2}} −\mathrm{8}×\mathrm{4}+\mathrm{20}=\mathrm{4} \\ $$$$ \\ $$
Commented by mr W last updated on 23/Jan/20

$${f}_{{min}} \neq\mathrm{40}\:{but}\:=\mathrm{4}. \\ $$
