
Question Number 78399 by john santu last updated on 17/Jan/20

$${dear}\:{sir}\:{W},\:{Mjs}\: \\ $$$${the}\:{set}\:\left\{\mathrm{1},\mathrm{4},{n}\right\}\:{have}\:{the}\:{condition}\:{that}\: \\ $$$${if}\:{two}\:{different}\:{elements}\:{are} \\ $$$${selected}\:{and}\:\mathrm{2112}\:{is}\:{added}\:{to} \\ $$$${the}\:{result}\:,\:{then}\:{the}\:{result}\: \\ $$$${is}\:{a}\:{perfect}\:{square}\:{if}\:{n}\:{is}\:{a}\: \\ $$$${positif}\:{number}\:.\:{then}\:{the}\:{number}\: \\ $$$${of}\:{possible}\:{values}\:{of}\:{n}\:{is}\: \\ $$$$\left({A}\right)\:\mathrm{8}\:\:\:\:\left({B}\right)\:\mathrm{7}\:\:\:\:\:\left({C}\right)\:\mathrm{6}\:\:\:\:\:\left({D}\right)\:\mathrm{5} \\ $$$$\left({E}\right)\:\mathrm{4} \\ $$
Commented by mr W last updated on 17/Jan/20

$${question}\:{is}\:{not}\:{clear}! \\ $$$${what}\:{means}\:``{two}\:{different}\:{elements} \\ $$$${are}\:{selectet}\:{and}\:\mathrm{2112}\:{is}\:{added}\:{to}\:{the} \\ $$$${result}''\:{when}\:{two}\:{different}\:{elements} \\ $$$${are}\:{selected},\:{say}\:\mathrm{1}\:{and}\:\mathrm{4},\:{what}\:{is}\:{the} \\ $$$${result}?\:{the}\:{sum}\:{of}\:{these}\:{two}\:{elements} \\ $$$${or}\:{the}\:{product}\:{of}\:{these}\:{elements}\:{or} \\ $$$${something}\:{else}? \\ $$$${please}\:{make}\:{the}\:{question}\:{clear}.\: \\ $$
Commented by john santu last updated on 17/Jan/20

$${the}\:{purpose}\:{of}\:{this}\:{problem}\: \\ $$$${is}\:{if}\:\mathrm{2}\:{members}\:{are}\:{selected} \\ $$$${from}\:{the}\:{set}\:{for}\:{example}\: \\ $$$$\mathrm{1}\:{and}\:{n}\:{then}\:\mathrm{1}×{n}\:+\:\mathrm{2112}\:{the} \\ $$$${result}\:{are}\:{quadratic}\:{number} \\ $$
Commented by mr W last updated on 17/Jan/20

$${now}\:{clear}!\:{so}\:{the}\:{question}\:{should}\:{be} \\ $$$$... \\ $$$${if}\:{two}\:{different}\:{elements}\:{are} \\ $$$${selected}\:{and}\:\mathrm{2112}\:{is}\:{added}\:{to} \\ $$$${their}\:{product}\:,\:{then}\:{the}\:{result}\: \\ $$$$... \\ $$
Commented by john santu last updated on 17/Jan/20
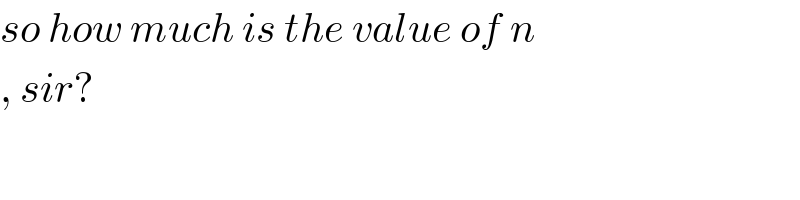
$${so}\:{how}\:{much}\:{is}\:{the}\:{value}\:{of}\:{n} \\ $$$$,\:{sir}? \\ $$
Commented by john santu last updated on 17/Jan/20
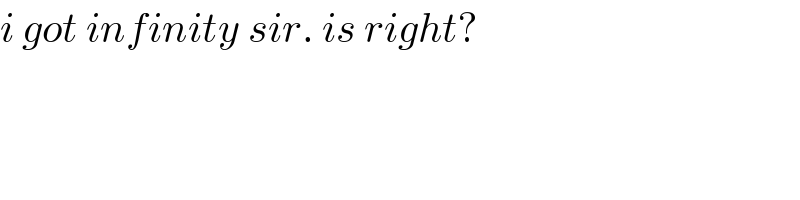
$${i}\:{got}\:{infinity}\:{sir}.\:{is}\:{right}? \\ $$
Commented by MJS last updated on 17/Jan/20
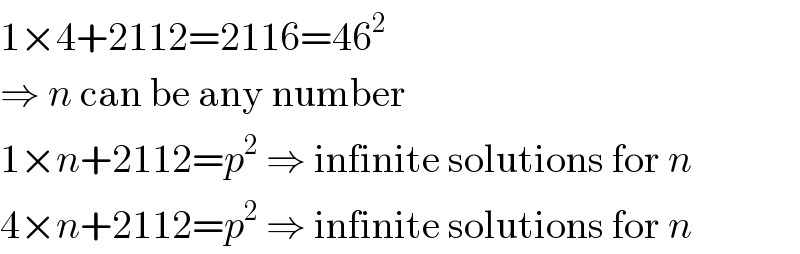
$$\mathrm{1}×\mathrm{4}+\mathrm{2112}=\mathrm{2116}=\mathrm{46}^{\mathrm{2}} \\ $$$$\Rightarrow\:{n}\:\mathrm{can}\:\mathrm{be}\:\mathrm{any}\:\mathrm{number} \\ $$$$\mathrm{1}×{n}+\mathrm{2112}={p}^{\mathrm{2}} \:\Rightarrow\:\mathrm{infinite}\:\mathrm{solutions}\:\mathrm{for}\:{n} \\ $$$$\mathrm{4}×{n}+\mathrm{2112}={p}^{\mathrm{2}} \:\Rightarrow\:\mathrm{infinite}\:\mathrm{solutions}\:\mathrm{for}\:{n} \\ $$
Commented by john santu last updated on 17/Jan/20
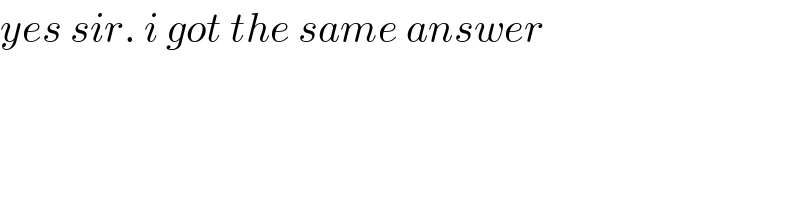
$${yes}\:{sir}.\:{i}\:{got}\:{the}\:{same}\:{answer} \\ $$
Commented by mr W last updated on 17/Jan/20
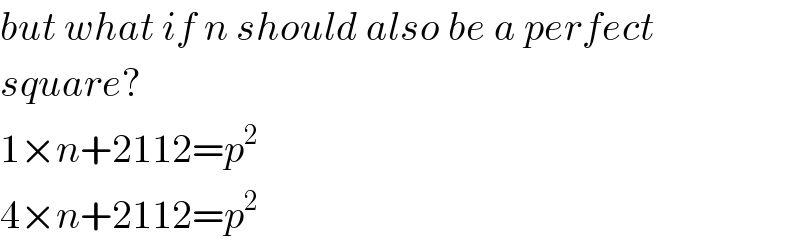
$${but}\:{what}\:{if}\:{n}\:{should}\:{also}\:{be}\:{a}\:{perfect} \\ $$$${square}? \\ $$$$\mathrm{1}×{n}+\mathrm{2112}={p}^{\mathrm{2}} \\ $$$$\mathrm{4}×{n}+\mathrm{2112}={p}^{\mathrm{2}} \\ $$
Commented by john santu last updated on 17/Jan/20
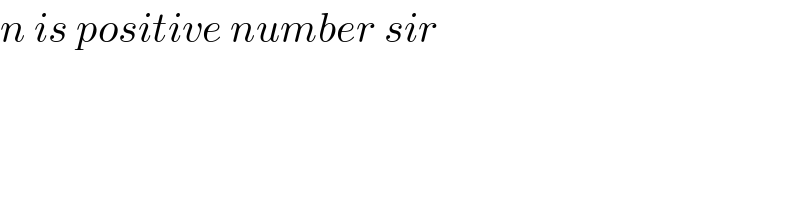
$${n}\:{is}\:{positive}\:{number}\:{sir} \\ $$
Commented by mr W last updated on 17/Jan/20
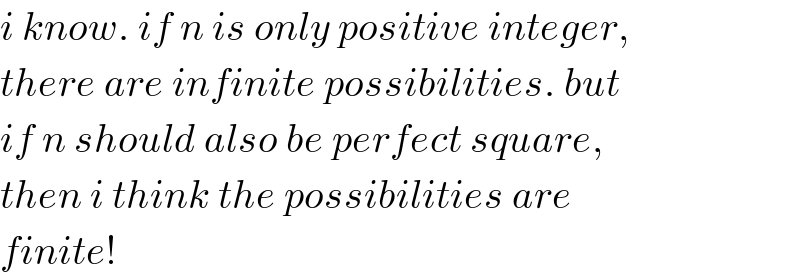
$${i}\:{know}.\:{if}\:{n}\:{is}\:{only}\:{positive}\:{integer}, \\ $$$${there}\:{are}\:{infinite}\:{possibilities}.\:{but} \\ $$$${if}\:{n}\:{should}\:{also}\:{be}\:{perfect}\:{square}, \\ $$$${then}\:{i}\:{think}\:{the}\:{possibilities}\:{are} \\ $$$${finite}! \\ $$
Commented by MJS last updated on 17/Jan/20

$$\mathrm{let}\:{n}=\left({p}−{q}\right)^{\mathrm{2}} \\ $$$$\left(\mathrm{1}\right)\:\:\left({p}−{q}\right)^{\mathrm{2}} +\mathrm{2112}={p}^{\mathrm{2}} \:\Rightarrow\:{p}=\frac{{q}^{\mathrm{2}} +\mathrm{2112}}{\mathrm{2}{q}} \\ $$$${p},\:{q}\in\mathbb{N}\wedge\mathrm{0}<{q}\leqslant{p}\:\Rightarrow\:\mathrm{0}<{q}\leqslant\mathrm{45} \\ $$$$\Rightarrow \\ $$$${q}\in\left\{\mathrm{2},\:\mathrm{4},\:\mathrm{6},\:\mathrm{8},\:\mathrm{12},\:\mathrm{16},\:\mathrm{22},\:\mathrm{24},\:\mathrm{32},\:\mathrm{44}\right\} \\ $$$${p}\in\left\{\mathrm{529},\:\mathrm{266},\:\mathrm{179},\:\mathrm{136},\:\mathrm{94},\:\mathrm{74},\:\mathrm{59},\:\mathrm{56},\:\mathrm{49},\:\mathrm{46}\right\} \\ $$$${n}\in\left\{\mathrm{277729},\:\mathrm{68644},\:\mathrm{29929},\:\mathrm{16384},\:\mathrm{6724},\:\mathrm{3364},\:\mathrm{1369},\:\mathrm{1024},\:\mathrm{289},\:\mathrm{4}\right\} \\ $$$$ \\ $$$$\left(\mathrm{2}\right)\:\:\mathrm{4}\left({p}−{q}\right)^{\mathrm{2}} +\mathrm{2112}={p}^{\mathrm{2}} \:\Rightarrow\:{q}={p}−\frac{\sqrt{{p}^{\mathrm{2}} −\mathrm{2112}}}{\mathrm{2}} \\ $$$$\Rightarrow \\ $$$${p}\in\left\{\mathrm{46},\:\mathrm{56},\:\mathrm{74},\:\mathrm{94},\:\mathrm{136},\:\mathrm{266}\right\} \\ $$$${q}\in\left\{\mathrm{45},\:\mathrm{40},\:\mathrm{45},\:\mathrm{53},\:\mathrm{72},\:\mathrm{135}\right\} \\ $$$${n}\in\left\{\mathrm{17161},\:\mathrm{4096},\:\mathrm{1681},\:\mathrm{841},\:\mathrm{256},\:\mathrm{1}\right\} \\ $$$$ \\ $$$$\mathrm{still}\:\mathrm{infinite}\:\mathrm{possibilities}\:\mathrm{for}\:{n}\:\mathrm{with} \\ $$$$\mathrm{1}×\mathrm{4}+\mathrm{2112}=\mathrm{46}^{\mathrm{2}} \\ $$
Commented by Rasheed.Sindhi last updated on 17/Jan/20
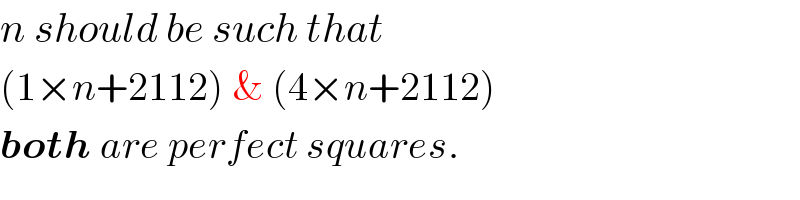
$${n}\:{should}\:{be}\:{such}\:{that} \\ $$$$\left(\mathrm{1}×{n}+\mathrm{2112}\right)\:\&\:\left(\mathrm{4}×{n}+\mathrm{2112}\right) \\ $$$$\boldsymbol{{both}}\:{are}\:{perfect}\:{squares}. \\ $$
Commented by john santu last updated on 17/Jan/20
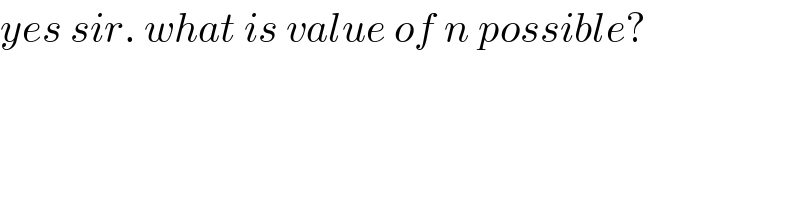
$${yes}\:{sir}.\:{what}\:{is}\:{value}\:{of}\:{n}\:{possible}? \\ $$$$ \\ $$
Commented by john santu last updated on 17/Jan/20
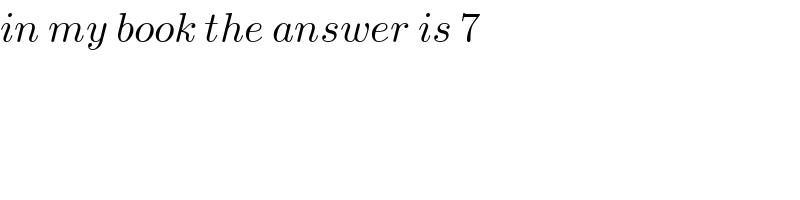
$${in}\:{my}\:{book}\:{the}\:{answer}\:{is}\:\mathrm{7} \\ $$
Answered by john santu last updated on 17/Jan/20
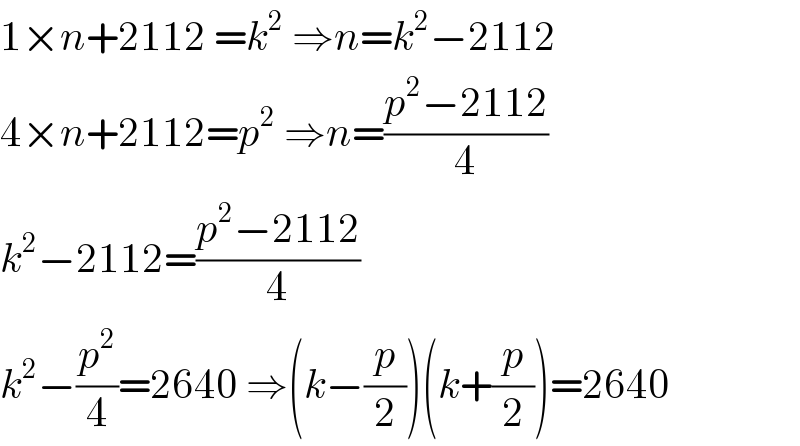
$$\mathrm{1}×{n}+\mathrm{2112}\:={k}^{\mathrm{2}} \:\Rightarrow{n}={k}^{\mathrm{2}} −\mathrm{2112} \\ $$$$\mathrm{4}×{n}+\mathrm{2112}={p}^{\mathrm{2}} \:\Rightarrow{n}=\frac{{p}^{\mathrm{2}} −\mathrm{2112}}{\mathrm{4}} \\ $$$${k}^{\mathrm{2}} −\mathrm{2112}=\frac{{p}^{\mathrm{2}} −\mathrm{2112}}{\mathrm{4}} \\ $$$${k}^{\mathrm{2}} −\frac{{p}^{\mathrm{2}} }{\mathrm{4}}=\mathrm{2640}\:\Rightarrow\left({k}−\frac{{p}}{\mathrm{2}}\right)\left({k}+\frac{{p}}{\mathrm{2}}\right)=\mathrm{2640} \\ $$
Commented by Rasheed.Sindhi last updated on 17/Jan/20
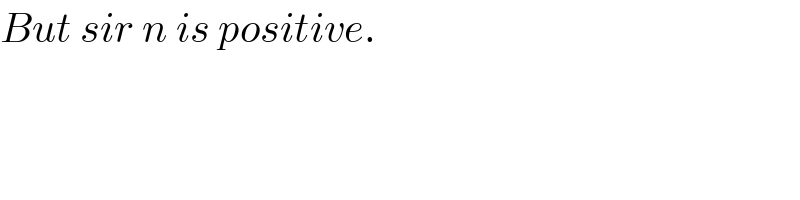
$${But}\:{sir}\:{n}\:{is}\:{positive}. \\ $$
Commented by MJS last updated on 17/Jan/20

$$\mathrm{yes}.\:\mathrm{I}\:\mathrm{posted}\:{all}\:\mathrm{9}\:\mathrm{solutions},\:\mathrm{then}\:\mathrm{I}\:\mathrm{wrote}\:\mathrm{the} \\ $$$$\mathrm{last}\:\mathrm{2}\:\mathrm{lines}... \\ $$
Commented by MJS last updated on 17/Jan/20

$$\mathrm{error}\:\mathrm{in}\:\mathrm{last}\:\mathrm{line} \\ $$$${k}^{\mathrm{2}} −\frac{{p}^{\mathrm{2}} }{\mathrm{4}}=\mathrm{1584} \\ $$$$\mathrm{your}\:\mathrm{idea}\:\mathrm{is}\:\mathrm{good},\:\mathrm{it}\:\mathrm{leads}\:\mathrm{to} \\ $$$${n}\in\left\{−\mathrm{512},\:−\mathrm{87},\:\mathrm{97},\:\mathrm{697},\:\mathrm{3072},\:\mathrm{8497},\:\mathrm{16113},\:\mathrm{37888},\:\mathrm{155497}\right\} \\ $$$$\mathrm{since}\:\mathrm{we}'\mathrm{re}\:\mathrm{looking}\:\mathrm{for}\:{n}\in\mathbb{N}\:\mathrm{we}\:\mathrm{have}\:\mathrm{indeed} \\ $$$$\mathrm{7}\:\mathrm{solutions} \\ $$
Commented by john santu last updated on 17/Jan/20
$${waw}..{thanks}\:{you}\:{sir} \\ $$
Answered by Rasheed.Sindhi last updated on 17/Jan/20

$$\Rightarrow\begin{cases}{\mathrm{1}×\mathrm{4}+\mathrm{2112}=\mathrm{46}^{\mathrm{2}} }\\{\mathrm{1}×{n}+\mathrm{2112}\:{is}\:{perfect}\:{square}}\\{\mathrm{4}×{n}+\mathrm{2112}\:{is}\:{perfect}\:{square}}\end{cases} \\ $$$$\:\:\:\:\:\:\:\:\mathrm{4}×{n}+\mathrm{2112}\:{is}\:{perfect}\:{square} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\Rightarrow{n}+\mathrm{528}\:{is}\:{perfect}\:{square} \\ $$$$\Rightarrow\begin{cases}{{n}+\mathrm{2112}\:{is}\:{perfect}\:{square}}\\{{n}+\mathrm{528}\:{is}\:{perfect}\:{square}}\end{cases} \\ $$$${Let}\:{n}+\mathrm{528}={q}^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:{n}+\mathrm{2112}={n}+\mathrm{528}+\mathrm{1584}={p}^{\mathrm{2}} >{q}^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:{q}^{\mathrm{2}} +\mathrm{1584}={p}^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\left({p}+{q}\right)\left({p}−{q}\right)=\mathrm{1584}=\mathrm{2}^{\mathrm{4}} .\mathrm{3}^{\mathrm{2}} .\mathrm{11} \\ $$$${p},{q}\in\mathbb{Z}^{+} \wedge\:{p}>{q}\Rightarrow{p}+{q}>{p}−{q} \\ $$$$\bullet{For}\:{p},{q}\:{being}\:{whole}\:{numbers} \\ $$$${p}+{q}\:{and}\:{p}−{q}\:{are}\:{both}\:{even}. \\ $$$$ \\ $$$${p}+{q}=\mathrm{44}\Rightarrow{p}−{q}=\mathrm{36} \\ $$$${p}+{q}=\mathrm{48}\Rightarrow{p}−{q}=\mathrm{33}\:\left({rejected}\right) \\ $$$${p}+{q}=\mathrm{66}\Rightarrow{p}−{q}=\mathrm{24} \\ $$$${p}+{q}=\mathrm{88}\Rightarrow{p}−{q}=\mathrm{18} \\ $$$${Continue} \\ $$
Commented by john santu last updated on 17/Jan/20

$${thanks}\:{you}\: \\ $$
