
Question Number 77309 by TawaTawa last updated on 05/Jan/20
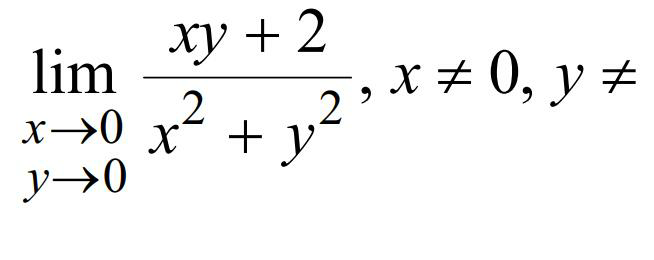
Commented by mr W last updated on 05/Jan/20

$$=\infty \\ $$
Commented by mathmax by abdo last updated on 05/Jan/20
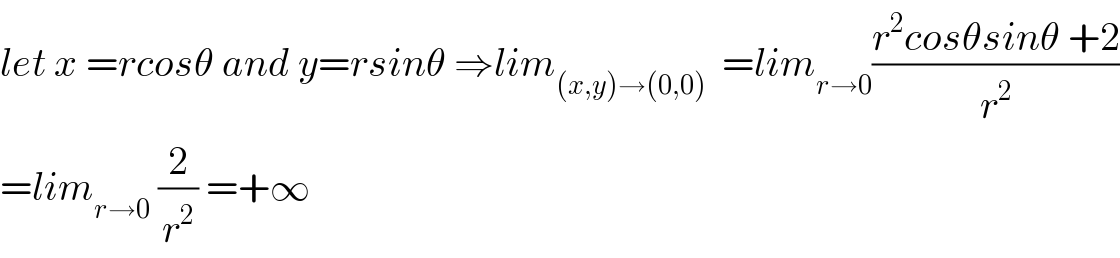
$${let}\:{x}\:={rcos}\theta\:{and}\:{y}={rsin}\theta\:\Rightarrow{lim}_{\left({x},{y}\right)\rightarrow\left(\mathrm{0},\mathrm{0}\right)} \:\:={lim}_{{r}\rightarrow\mathrm{0}} \frac{{r}^{\mathrm{2}} {cos}\theta{sin}\theta\:+\mathrm{2}}{{r}^{\mathrm{2}} } \\ $$$$={lim}_{{r}\rightarrow\mathrm{0}} \:\frac{\mathrm{2}}{{r}^{\mathrm{2}} }\:=+\infty \\ $$
Commented by TawaTawa last updated on 05/Jan/20
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$
Commented by mathmax by abdo last updated on 05/Jan/20

$${you}\:{are}\:{welcome} \\ $$
Answered by MJS last updated on 05/Jan/20
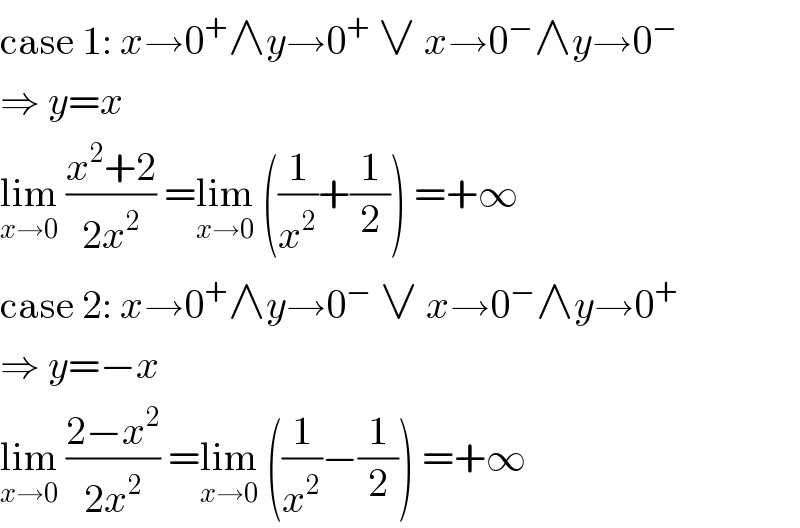
$$\mathrm{case}\:\mathrm{1}:\:{x}\rightarrow\mathrm{0}^{+} \wedge{y}\rightarrow\mathrm{0}^{+} \:\vee\:{x}\rightarrow\mathrm{0}^{−} \wedge{y}\rightarrow\mathrm{0}^{−} \\ $$$$\Rightarrow\:{y}={x} \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{{x}^{\mathrm{2}} +\mathrm{2}}{\mathrm{2}{x}^{\mathrm{2}} }\:=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\left(\frac{\mathrm{1}}{{x}^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{2}}\right)\:=+\infty \\ $$$$\mathrm{case}\:\mathrm{2}:\:{x}\rightarrow\mathrm{0}^{+} \wedge{y}\rightarrow\mathrm{0}^{−} \:\vee\:{x}\rightarrow\mathrm{0}^{−} \wedge{y}\rightarrow\mathrm{0}^{+} \\ $$$$\Rightarrow\:{y}=−{x} \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{2}−{x}^{\mathrm{2}} }{\mathrm{2}{x}^{\mathrm{2}} }\:=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\left(\frac{\mathrm{1}}{{x}^{\mathrm{2}} }−\frac{\mathrm{1}}{\mathrm{2}}\right)\:=+\infty \\ $$
Commented by TawaTawa last updated on 05/Jan/20
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$
