
Question Number 77219 by john santu last updated on 04/Jan/20
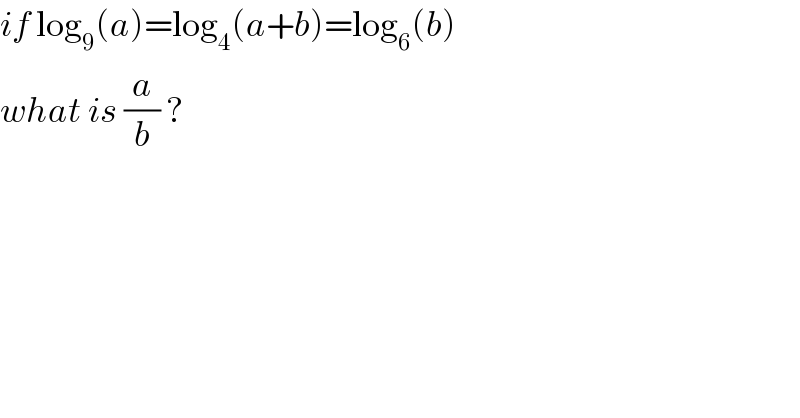
$${if}\:\mathrm{log}_{\mathrm{9}} \left({a}\right)=\mathrm{log}_{\mathrm{4}} \left({a}+{b}\right)=\mathrm{log}_{\mathrm{6}} \left({b}\right)\: \\ $$$${what}\:{is}\:\frac{{a}}{{b}}\:? \\ $$
Answered by jagoll last updated on 04/Jan/20
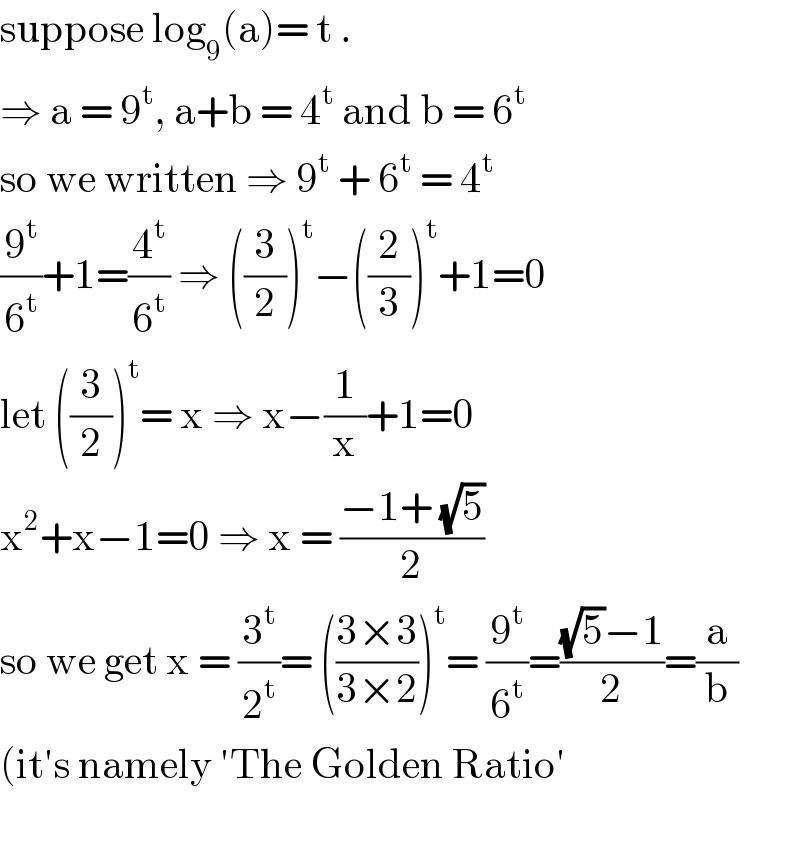
$$\mathrm{suppose}\:\mathrm{log}_{\mathrm{9}} \left(\mathrm{a}\right)=\:\mathrm{t}\:. \\ $$$$\Rightarrow\:\mathrm{a}\:=\:\mathrm{9}^{\mathrm{t}} ,\:\mathrm{a}+\mathrm{b}\:=\:\mathrm{4}^{\mathrm{t}} \:\mathrm{and}\:\mathrm{b}\:=\:\mathrm{6}^{\mathrm{t}} \\ $$$$\mathrm{so}\:\mathrm{we}\:\mathrm{written}\:\Rightarrow\:\mathrm{9}^{\mathrm{t}} \:+\:\mathrm{6}^{\mathrm{t}} \:=\:\mathrm{4}^{\mathrm{t}\:} \\ $$$$\frac{\mathrm{9}^{\mathrm{t}} }{\mathrm{6}^{\mathrm{t}} }+\mathrm{1}=\frac{\mathrm{4}^{\mathrm{t}} }{\mathrm{6}^{\mathrm{t}} }\:\Rightarrow\:\left(\frac{\mathrm{3}}{\mathrm{2}}\right)^{\mathrm{t}} −\left(\frac{\mathrm{2}}{\mathrm{3}}\right)^{\mathrm{t}} +\mathrm{1}=\mathrm{0} \\ $$$$\mathrm{let}\:\left(\frac{\mathrm{3}}{\mathrm{2}}\right)^{\mathrm{t}} =\:\mathrm{x}\:\Rightarrow\:\mathrm{x}−\frac{\mathrm{1}}{\mathrm{x}}+\mathrm{1}=\mathrm{0} \\ $$$$\mathrm{x}^{\mathrm{2}} +\mathrm{x}−\mathrm{1}=\mathrm{0}\:\Rightarrow\:\mathrm{x}\:=\:\frac{−\mathrm{1}+\:\sqrt{\mathrm{5}}}{\mathrm{2}} \\ $$$$\mathrm{so}\:\mathrm{we}\:\mathrm{get}\:\mathrm{x}\:=\:\frac{\mathrm{3}^{\mathrm{t}} }{\mathrm{2}^{\mathrm{t}} }=\:\left(\frac{\mathrm{3}×\mathrm{3}}{\mathrm{3}×\mathrm{2}}\right)^{\mathrm{t}} =\:\frac{\mathrm{9}^{\mathrm{t}} }{\mathrm{6}^{\mathrm{t}} }=\frac{\sqrt{\mathrm{5}}−\mathrm{1}}{\mathrm{2}}=\frac{\mathrm{a}}{\mathrm{b}} \\ $$$$\left(\mathrm{it}'\mathrm{s}\:\mathrm{namely}\:'\mathrm{The}\:\mathrm{Golden}\:\mathrm{Ratio}'\right. \\ $$$$ \\ $$
Commented by jagoll last updated on 04/Jan/20

$$\approx\:\mathrm{0}.\mathrm{6180} \\ $$
Commented by john santu last updated on 05/Jan/20

$${thanks}\:{you} \\ $$
