
Question Number 7612 by Tawakalitu. last updated on 06/Sep/16
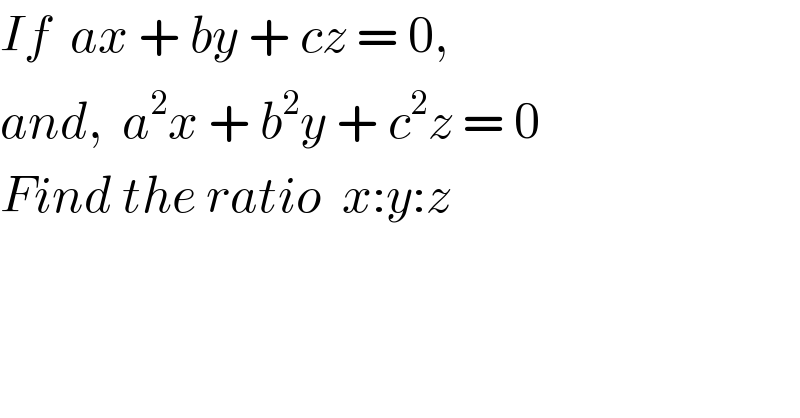
$${If}\:\:{ax}\:+\:{by}\:+\:{cz}\:=\:\mathrm{0},\: \\ $$$${and},\:\:{a}^{\mathrm{2}} {x}\:+\:{b}^{\mathrm{2}} {y}\:+\:{c}^{\mathrm{2}} {z}\:=\:\mathrm{0} \\ $$$${Find}\:{the}\:{ratio}\:\:{x}:{y}:{z} \\ $$
Commented by Rasheed Soomro last updated on 06/Sep/16
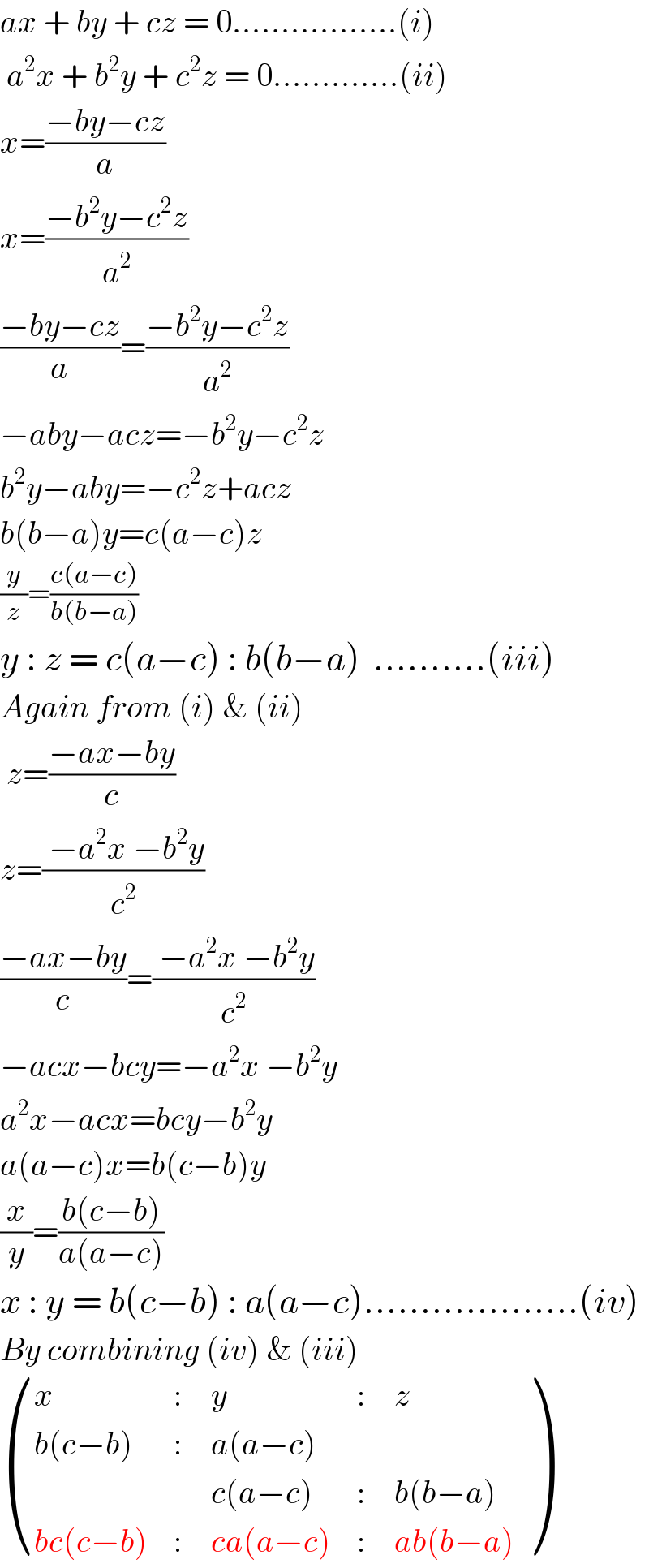
$${ax}\:+\:{by}\:+\:{cz}\:=\:\mathrm{0}.................\left({i}\right) \\ $$$$\:{a}^{\mathrm{2}} {x}\:+\:{b}^{\mathrm{2}} {y}\:+\:{c}^{\mathrm{2}} {z}\:=\:\mathrm{0}.............\left({ii}\right) \\ $$$${x}=\frac{−{by}−{cz}}{{a}} \\ $$$${x}=\frac{−{b}^{\mathrm{2}} {y}−{c}^{\mathrm{2}} {z}}{{a}^{\mathrm{2}} } \\ $$$$\frac{−{by}−{cz}}{{a}}=\frac{−{b}^{\mathrm{2}} {y}−{c}^{\mathrm{2}} {z}}{{a}^{\mathrm{2}} } \\ $$$$−{aby}−{acz}=−{b}^{\mathrm{2}} {y}−{c}^{\mathrm{2}} {z} \\ $$$${b}^{\mathrm{2}} {y}−{aby}=−{c}^{\mathrm{2}} {z}+{acz} \\ $$$${b}\left({b}−{a}\right){y}={c}\left({a}−{c}\right){z} \\ $$$$\frac{{y}}{{z}}=\frac{{c}\left({a}−{c}\right)}{{b}\left({b}−{a}\right)} \\ $$$${y}\::\:{z}\:=\:{c}\left({a}−{c}\right)\::\:{b}\left({b}−{a}\right)\:\:..........\left({iii}\right) \\ $$$${Again}\:{from}\:\left({i}\right)\:\&\:\left({ii}\right) \\ $$$$\:{z}=\frac{−{ax}−{by}}{{c}} \\ $$$${z}=\frac{\:−{a}^{\mathrm{2}} {x}\:−{b}^{\mathrm{2}} {y}}{{c}^{\mathrm{2}} } \\ $$$$\frac{−{ax}−{by}}{{c}}=\frac{\:−{a}^{\mathrm{2}} {x}\:−{b}^{\mathrm{2}} {y}}{{c}^{\mathrm{2}} } \\ $$$$−{acx}−{bcy}=−{a}^{\mathrm{2}} {x}\:−{b}^{\mathrm{2}} {y} \\ $$$${a}^{\mathrm{2}} {x}−{acx}={bcy}−{b}^{\mathrm{2}} {y} \\ $$$${a}\left({a}−{c}\right){x}={b}\left({c}−{b}\right){y} \\ $$$$\frac{{x}}{{y}}=\frac{{b}\left({c}−{b}\right)}{{a}\left({a}−{c}\right)} \\ $$$${x}\::\:{y}\:=\:{b}\left({c}−{b}\right)\::\:{a}\left({a}−{c}\right)...................\left({iv}\right) \\ $$$${By}\:{combining}\:\left({iv}\right)\:\&\:\left({iii}\right) \\ $$$$\begin{pmatrix}{{x}}&{:}&{{y}}&{:}&{{z}}\\{{b}\left({c}−{b}\right)}&{:}&{{a}\left({a}−{c}\right)}&{}&{}\\{}&{}&{{c}\left({a}−{c}\right)}&{:}&{{b}\left({b}−{a}\right)}\\{{bc}\left({c}−{b}\right)}&{:}&{{ca}\left({a}−{c}\right)}&{:}&{{ab}\left({b}−{a}\right)}\end{pmatrix} \\ $$
Commented by Tawakalitu. last updated on 06/Sep/16
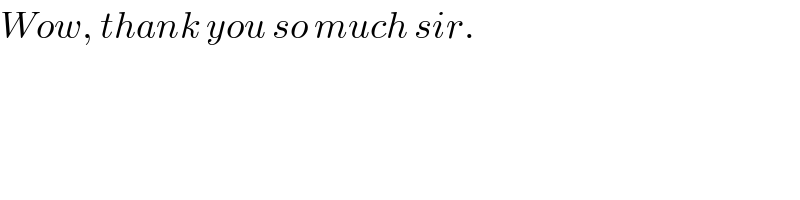
$${Wow},\:{thank}\:{you}\:{so}\:{much}\:{sir}. \\ $$
Commented by Tawakalitu. last updated on 06/Sep/16
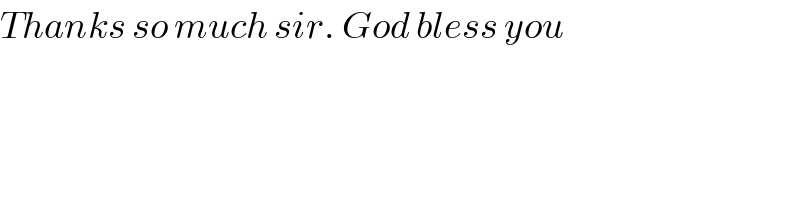
$${Thanks}\:{so}\:{much}\:{sir}.\:{God}\:{bless}\:{you} \\ $$
Answered by Yozzia last updated on 06/Sep/16
$${Answer}\:{in}\:{comments}. \\ $$
