
Question Number 7608 by Tawakalitu. last updated on 06/Sep/16
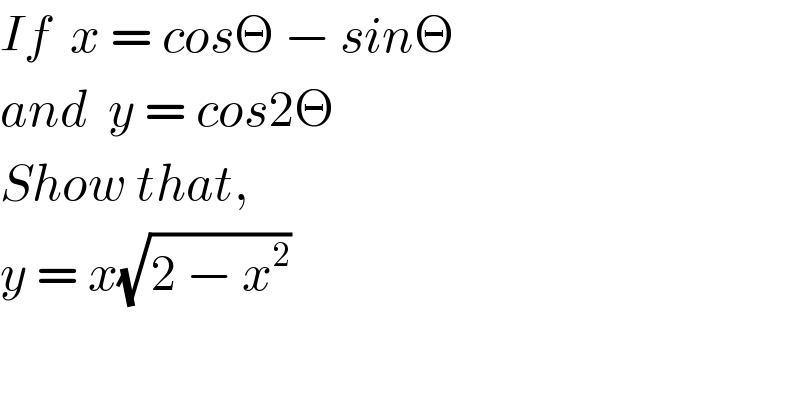
$${If}\:\:{x}\:=\:{cos}\Theta\:−\:{sin}\Theta \\ $$$${and}\:\:{y}\:=\:{cos}\mathrm{2}\Theta \\ $$$${Show}\:{that},\:\: \\ $$$${y}\:=\:{x}\sqrt{\mathrm{2}\:−\:{x}^{\mathrm{2}} } \\ $$
Commented by sou1618 last updated on 06/Sep/16
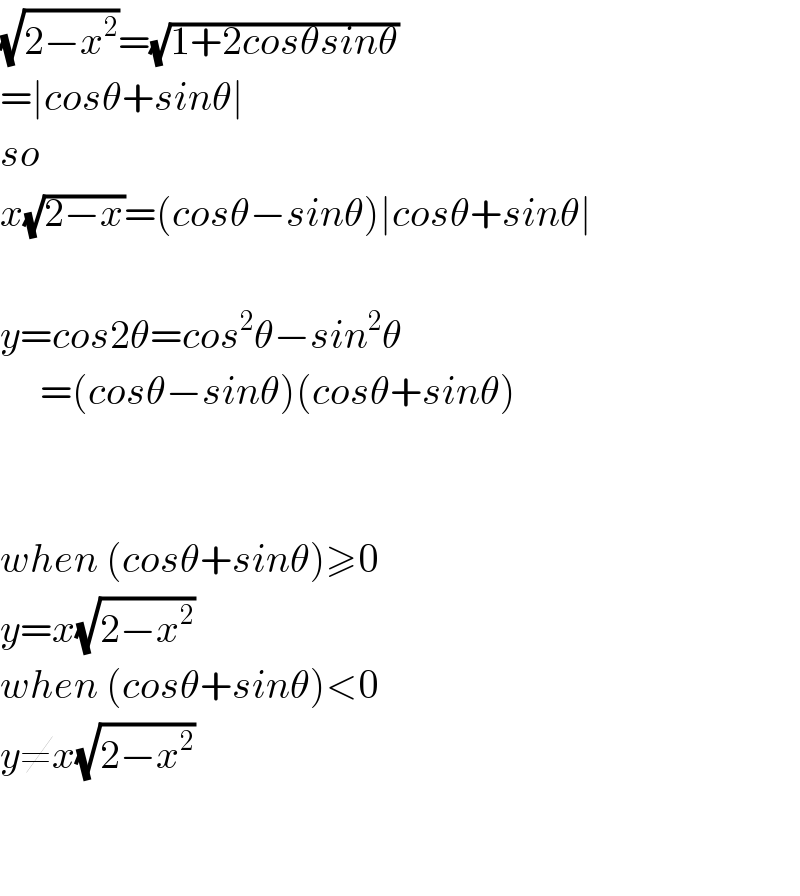
$$\sqrt{\mathrm{2}−{x}^{\mathrm{2}} }=\sqrt{\mathrm{1}+\mathrm{2}{cos}\theta{sin}\theta} \\ $$$$=\mid{cos}\theta+{sin}\theta\mid \\ $$$${so} \\ $$$${x}\sqrt{\mathrm{2}−{x}}=\left({cos}\theta−{sin}\theta\right)\mid{cos}\theta+{sin}\theta\mid \\ $$$$ \\ $$$${y}={cos}\mathrm{2}\theta={cos}^{\mathrm{2}} \theta−{sin}^{\mathrm{2}} \theta \\ $$$$\:\:\:\:\:=\left({cos}\theta−{sin}\theta\right)\left({cos}\theta+{sin}\theta\right) \\ $$$$ \\ $$$$ \\ $$$${when}\:\left({cos}\theta+{sin}\theta\right)\geqslant\mathrm{0} \\ $$$${y}={x}\sqrt{\mathrm{2}−{x}^{\mathrm{2}} } \\ $$$${when}\:\left({cos}\theta+{sin}\theta\right)<\mathrm{0} \\ $$$${y}\neq{x}\sqrt{\mathrm{2}−{x}^{\mathrm{2}} } \\ $$$$ \\ $$$$ \\ $$
Commented by Tawakalitu. last updated on 06/Sep/16

$${Thank}\:{you}\:{sir} \\ $$
Commented by Tawakalitu. last updated on 06/Sep/16

$${i}\:{appreciate} \\ $$
Answered by sandy_suhendra last updated on 06/Sep/16

$${x}\sqrt{\mathrm{2}−{x}^{\mathrm{2}} } \\ $$$$=\left({cos}\theta−{sin}\theta\right)\sqrt{\mathrm{2}\left({cos}^{\mathrm{2}} \theta+{sin}^{\mathrm{2}} \theta\right)−\left({cos}\theta−{sin}\theta\right)^{\mathrm{2}} } \\ $$$$\left.=\left({cos}\theta−{sin}\theta\right)\sqrt{\left.\mathrm{2}{cos}^{\mathrm{2}} \theta+\mathrm{2}{sin}^{\mathrm{2}} \theta\right)−\left({cos}^{\mathrm{2}} \theta+{sin}^{\mathrm{2}} \theta−\mathrm{2}{sin}\theta{cos}\theta\right.}\right) \\ $$$$=\left({cos}\theta−{sin}\theta\right)\sqrt{{cos}^{\mathrm{2}} \theta+{sin}^{\mathrm{2}} \theta+\mathrm{2}{sin}\theta{cos}\theta} \\ $$$$=\left({cos}\theta−{sin}\theta\right)\sqrt{\left({cos}\theta+{sin}\theta\right)^{\mathrm{2}} } \\ $$$$=\left({cos}\theta−{sin}\theta\right)\left({cos}\theta+{sin}\theta\right) \\ $$$$={cos}^{\mathrm{2}} \theta−{sin}^{\mathrm{2}} \theta \\ $$$$={cos}\mathrm{2}\theta \\ $$$$={y} \\ $$
Commented by Tawakalitu. last updated on 06/Sep/16
$${i}\:{really}\:{appreciate}\:{your}\:{effort}\:{sir}.\:{thanks}\:{so}\:{much}. \\ $$
Commented by sou1618 last updated on 06/Sep/16
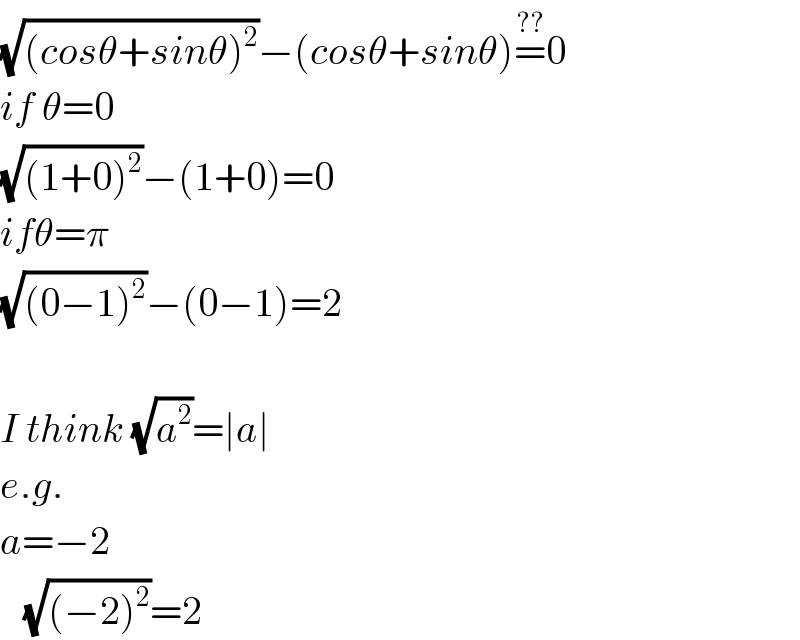
$$\sqrt{\left({cos}\theta+{sin}\theta\right)^{\mathrm{2}} }−\left({cos}\theta+{sin}\theta\right)\overset{??} {=}\mathrm{0} \\ $$$${if}\:\theta=\mathrm{0} \\ $$$$\sqrt{\left(\mathrm{1}+\mathrm{0}\right)^{\mathrm{2}} }−\left(\mathrm{1}+\mathrm{0}\right)=\mathrm{0} \\ $$$${if}\theta=\pi \\ $$$$\sqrt{\left(\mathrm{0}−\mathrm{1}\right)^{\mathrm{2}} }−\left(\mathrm{0}−\mathrm{1}\right)=\mathrm{2} \\ $$$$ \\ $$$${I}\:{think}\:\sqrt{{a}^{\mathrm{2}} }=\mid{a}\mid \\ $$$${e}.{g}. \\ $$$${a}=−\mathrm{2} \\ $$$$\:\:\:\sqrt{\left(−\mathrm{2}\right)^{\mathrm{2}} }=\mathrm{2} \\ $$
Commented by Rasheed Soomro last updated on 07/Sep/16

$${I}\:{agree}\:{with}\:{you}. \\ $$
