
Question Number 75955 by benjo last updated on 21/Dec/19

$${help}\:{me}\: \\ $$$$ \\ $$
Answered by benjo last updated on 21/Dec/19
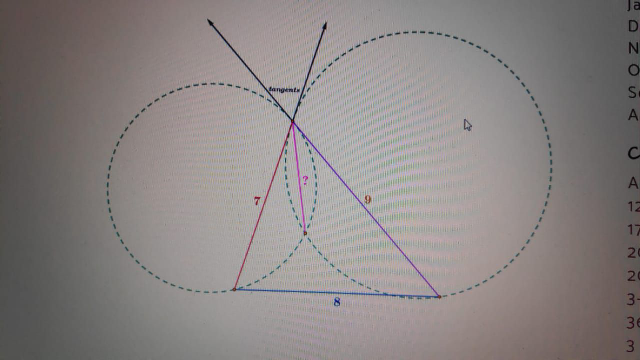
Answered by mr W last updated on 21/Dec/19
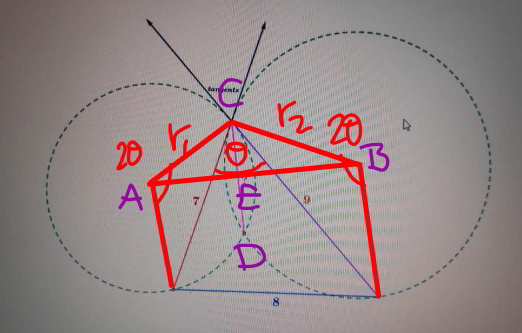
Commented by mr W last updated on 21/Dec/19
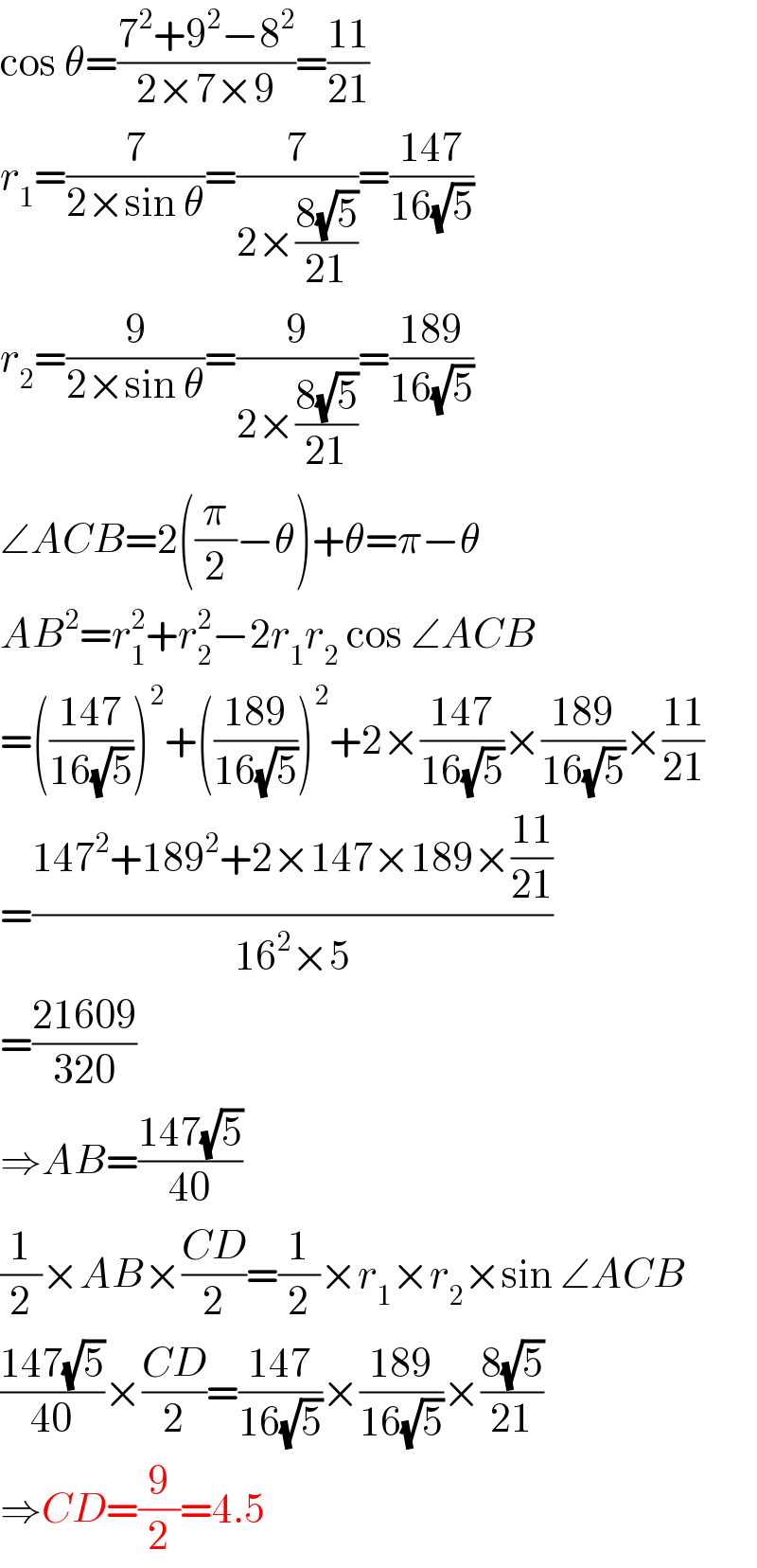
$$\mathrm{cos}\:\theta=\frac{\mathrm{7}^{\mathrm{2}} +\mathrm{9}^{\mathrm{2}} −\mathrm{8}^{\mathrm{2}} }{\mathrm{2}×\mathrm{7}×\mathrm{9}}=\frac{\mathrm{11}}{\mathrm{21}} \\ $$$${r}_{\mathrm{1}} =\frac{\mathrm{7}}{\mathrm{2}×\mathrm{sin}\:\theta}=\frac{\mathrm{7}}{\mathrm{2}×\frac{\mathrm{8}\sqrt{\mathrm{5}}}{\mathrm{21}}}=\frac{\mathrm{147}}{\mathrm{16}\sqrt{\mathrm{5}}} \\ $$$${r}_{\mathrm{2}} =\frac{\mathrm{9}}{\mathrm{2}×\mathrm{sin}\:\theta}=\frac{\mathrm{9}}{\mathrm{2}×\frac{\mathrm{8}\sqrt{\mathrm{5}}}{\mathrm{21}}}=\frac{\mathrm{189}}{\mathrm{16}\sqrt{\mathrm{5}}} \\ $$$$\angle{ACB}=\mathrm{2}\left(\frac{\pi}{\mathrm{2}}−\theta\right)+\theta=\pi−\theta \\ $$$${AB}^{\mathrm{2}} ={r}_{\mathrm{1}} ^{\mathrm{2}} +{r}_{\mathrm{2}} ^{\mathrm{2}} −\mathrm{2}{r}_{\mathrm{1}} {r}_{\mathrm{2}} \:\mathrm{cos}\:\angle{ACB} \\ $$$$=\left(\frac{\mathrm{147}}{\mathrm{16}\sqrt{\mathrm{5}}}\right)^{\mathrm{2}} +\left(\frac{\mathrm{189}}{\mathrm{16}\sqrt{\mathrm{5}}}\right)^{\mathrm{2}} +\mathrm{2}×\frac{\mathrm{147}}{\mathrm{16}\sqrt{\mathrm{5}}}×\frac{\mathrm{189}}{\mathrm{16}\sqrt{\mathrm{5}}}×\frac{\mathrm{11}}{\mathrm{21}} \\ $$$$=\frac{\mathrm{147}^{\mathrm{2}} +\mathrm{189}^{\mathrm{2}} +\mathrm{2}×\mathrm{147}×\mathrm{189}×\frac{\mathrm{11}}{\mathrm{21}}}{\mathrm{16}^{\mathrm{2}} ×\mathrm{5}} \\ $$$$=\frac{\mathrm{21609}}{\mathrm{320}} \\ $$$$\Rightarrow{AB}=\frac{\mathrm{147}\sqrt{\mathrm{5}}}{\mathrm{40}} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}×{AB}×\frac{{CD}}{\mathrm{2}}=\frac{\mathrm{1}}{\mathrm{2}}×{r}_{\mathrm{1}} ×{r}_{\mathrm{2}} ×\mathrm{sin}\:\angle{ACB} \\ $$$$\frac{\mathrm{147}\sqrt{\mathrm{5}}}{\mathrm{40}}×\frac{{CD}}{\mathrm{2}}=\frac{\mathrm{147}}{\mathrm{16}\sqrt{\mathrm{5}}}×\frac{\mathrm{189}}{\mathrm{16}\sqrt{\mathrm{5}}}×\frac{\mathrm{8}\sqrt{\mathrm{5}}}{\mathrm{21}} \\ $$$$\Rightarrow{CD}=\frac{\mathrm{9}}{\mathrm{2}}=\mathrm{4}.\mathrm{5} \\ $$
Commented by benjo last updated on 21/Dec/19

$$\mathrm{thanks}\:\mathrm{sir}.\: \\ $$
