
Question Number 7587 by ten last updated on 05/Sep/16
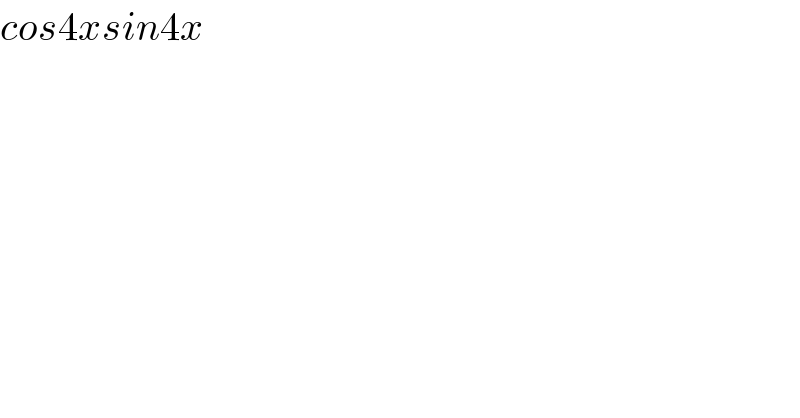
$${cos}\mathrm{4}{xsin}\mathrm{4}{x} \\ $$
Answered by Rasheed Soomro last updated on 05/Sep/16
![cos4xsin4x cos α sin β=(1/2)[sin(α+β)−sin(α−β)] cos 4x sin 4x=(1/2)[sin(4x+4x)−sin(4x−4x)] =(1/2)sin 8x Or cos 4x sin 4x=(1/2)(2cos 4x sin 4x) 2 sin θ cos θ =sin 2θ =(1/2)sin 8x](Q7597.png)
$${cos}\mathrm{4}{xsin}\mathrm{4}{x} \\ $$$$\mathrm{cos}\:\alpha\:\mathrm{sin}\:\beta=\left(\mathrm{1}/\mathrm{2}\right)\left[\mathrm{sin}\left(\alpha+\beta\right)−\mathrm{sin}\left(\alpha−\beta\right)\right]\:\: \\ $$$$\mathrm{cos}\:\mathrm{4}{x}\:\mathrm{sin}\:\mathrm{4}{x}=\left(\mathrm{1}/\mathrm{2}\right)\left[\mathrm{sin}\left(\mathrm{4}{x}+\mathrm{4}{x}\right)−\mathrm{sin}\left(\mathrm{4}{x}−\mathrm{4}{x}\right)\right]\:\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\left(\mathrm{1}/\mathrm{2}\right)\mathrm{sin}\:\mathrm{8}{x} \\ $$$${Or} \\ $$$$\mathrm{cos}\:\mathrm{4}{x}\:\mathrm{sin}\:\mathrm{4}{x}=\left(\mathrm{1}/\mathrm{2}\right)\left(\mathrm{2cos}\:\mathrm{4}{x}\:\mathrm{sin}\:\mathrm{4}{x}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{2}\:\mathrm{sin}\:\theta\:\mathrm{cos}\:\theta\:\:=\mathrm{sin}\:\mathrm{2}\theta \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\left(\mathrm{1}/\mathrm{2}\right)\mathrm{sin}\:\mathrm{8}{x} \\ $$$$ \\ $$
