
Question Number 73090 by ajfour last updated on 06/Nov/19
Commented by ajfour last updated on 06/Nov/19
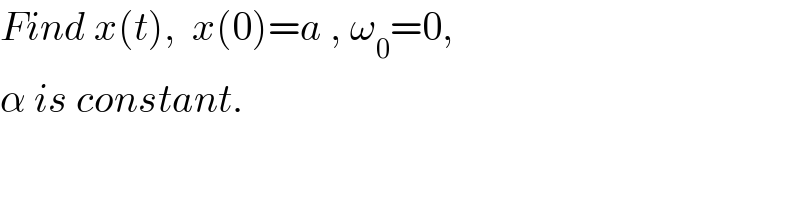
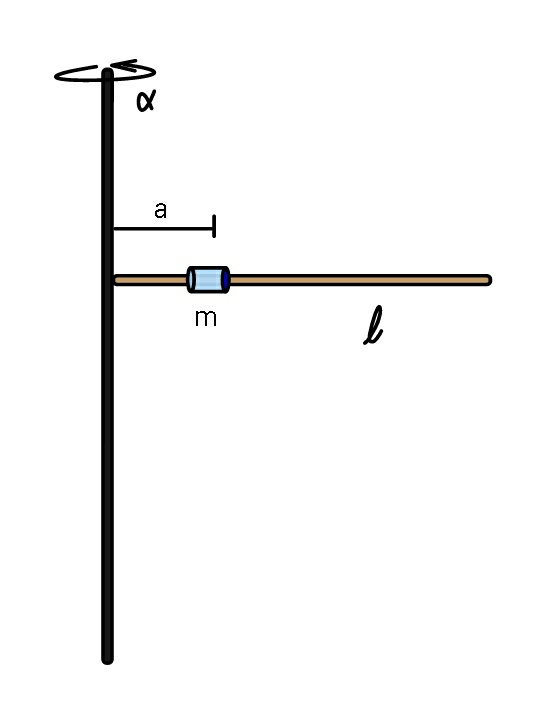
$${Find}\:{x}\left({t}\right),\:\:{x}\left(\mathrm{0}\right)={a}\:,\:\omega_{\mathrm{0}} =\mathrm{0},\: \\ $$$$\alpha\:{is}\:{constant}. \\ $$
Answered by mr W last updated on 06/Nov/19
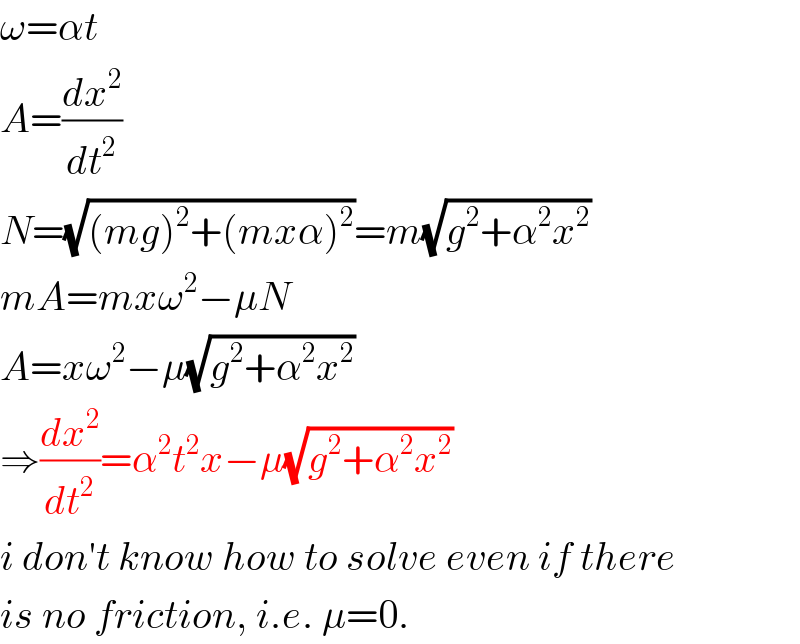
$$\omega=\alpha{t} \\ $$$${A}=\frac{{dx}^{\mathrm{2}} }{{dt}^{\mathrm{2}} } \\ $$$${N}=\sqrt{\left({mg}\right)^{\mathrm{2}} +\left({mx}\alpha\right)^{\mathrm{2}} }={m}\sqrt{{g}^{\mathrm{2}} +\alpha^{\mathrm{2}} {x}^{\mathrm{2}} } \\ $$$${mA}={mx}\omega^{\mathrm{2}} −\mu{N} \\ $$$${A}={x}\omega^{\mathrm{2}} −\mu\sqrt{{g}^{\mathrm{2}} +\alpha^{\mathrm{2}} {x}^{\mathrm{2}} } \\ $$$$\Rightarrow\frac{{dx}^{\mathrm{2}} }{{dt}^{\mathrm{2}} }=\alpha^{\mathrm{2}} {t}^{\mathrm{2}} {x}−\mu\sqrt{{g}^{\mathrm{2}} +\alpha^{\mathrm{2}} {x}^{\mathrm{2}} } \\ $$$${i}\:{don}'{t}\:{know}\:{how}\:{to}\:{solve}\:{even}\:{if}\:{there} \\ $$$${is}\:{no}\:{friction},\:{i}.{e}.\:\mu=\mathrm{0}. \\ $$
Commented by ajfour last updated on 06/Nov/19

$${alright}\:{sir},\:{has}\:{to}\:{do}\:{with} \\ $$$${coriolis}\:{acceleration},\:{perhaps}, \\ $$$${i}'{ll}\:{revise}\:{and}\:{update}\:{you}\:{too}.. \\ $$
Answered by ajfour last updated on 12/Nov/19

Commented by mr W last updated on 12/Nov/19

$${thank}\:{you}\:{sir}! \\ $$$${if}\:{the}\:{angular}\:{acceleration}\:{is}\:{zero}, \\ $$$${we}\:{can}\:{solve}\:{even}\:{with}\:{friction}. \\ $$$$ \\ $$$${but}\:{the}\:{solution}\:{for}\:\frac{{d}^{\mathrm{2}} {r}}{{dt}^{\mathrm{2}} }=\alpha^{\mathrm{2}} {rt}^{\mathrm{2}} \:{needs} \\ $$$${parabolic}\:{cylinder}\:{function}\:{which}\:{i} \\ $$$${don}'{t}\:{understand}. \\ $$
Commented by ajfour last updated on 12/Nov/19
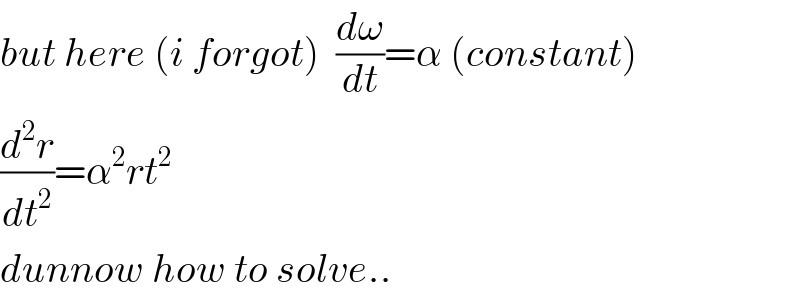
$${but}\:{here}\:\left({i}\:{forgot}\right)\:\:\frac{{d}\omega}{{dt}}=\alpha\:\left({constant}\right) \\ $$$$\frac{{d}^{\mathrm{2}} {r}}{{dt}^{\mathrm{2}} }=\alpha^{\mathrm{2}} {rt}^{\mathrm{2}} \\ $$$${dunnow}\:{how}\:{to}\:{solve}.. \\ $$
