
Previous in Relation and Functions Next in Relation and Functions
Question Number 70596 by mathmax by abdo last updated on 06/Oct/19
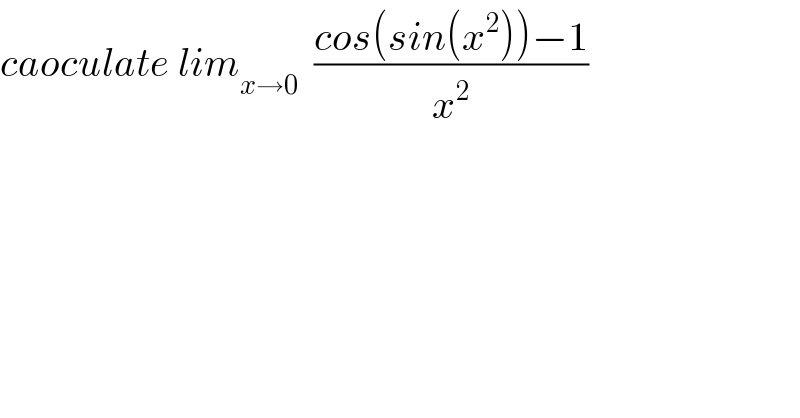
$${caoculate}\:{lim}_{{x}\rightarrow\mathrm{0}} \:\:\frac{{cos}\left({sin}\left({x}^{\mathrm{2}} \right)\right)−\mathrm{1}}{{x}^{\mathrm{2}} } \\ $$
Commented by mathmax by abdo last updated on 06/Oct/19
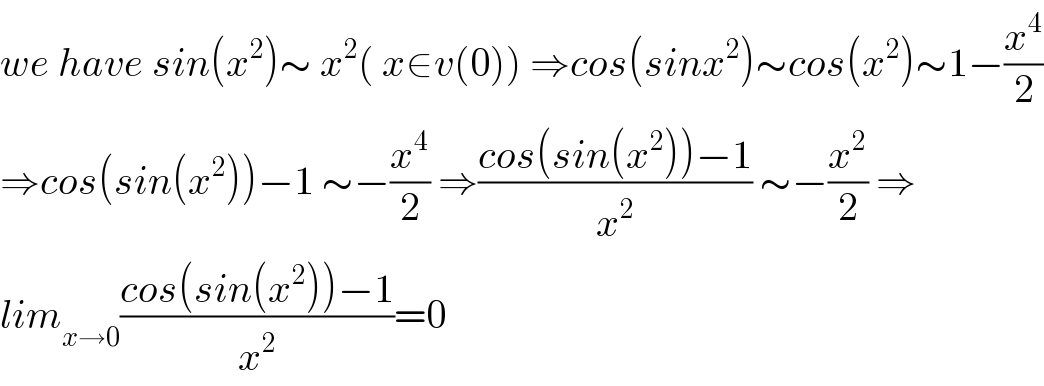
$${we}\:{have}\:{sin}\left({x}^{\mathrm{2}} \right)\sim\:{x}^{\mathrm{2}} \left(\:{x}\in{v}\left(\mathrm{0}\right)\right)\:\Rightarrow{cos}\left({sinx}^{\mathrm{2}} \right)\sim{cos}\left({x}^{\mathrm{2}} \right)\sim\mathrm{1}−\frac{{x}^{\mathrm{4}} }{\mathrm{2}} \\ $$$$\Rightarrow{cos}\left({sin}\left({x}^{\mathrm{2}} \right)\right)−\mathrm{1}\:\sim−\frac{{x}^{\mathrm{4}} }{\mathrm{2}}\:\Rightarrow\frac{{cos}\left({sin}\left({x}^{\mathrm{2}} \right)\right)−\mathrm{1}}{{x}^{\mathrm{2}} }\:\sim−\frac{{x}^{\mathrm{2}} }{\mathrm{2}}\:\Rightarrow \\ $$$${lim}_{{x}\rightarrow\mathrm{0}} \frac{{cos}\left({sin}\left({x}^{\mathrm{2}} \right)\right)−\mathrm{1}}{{x}^{\mathrm{2}} }=\mathrm{0} \\ $$
Answered by Henri Boucatchou last updated on 06/Oct/19
![lim_(x→0) ((cos(sinx^2 )−1)/x^2 ) = lim_(X→0) ((cos(sinX)−cos(sin0))/(X−0)) = cos(sinX)]′_((X=0)) = −cosXsin(sinX)]_((X=0)) = 0](Q70615.png)
$$\left.\underset{\boldsymbol{{x}}\rightarrow\mathrm{0}} {\boldsymbol{{l}}\left.\boldsymbol{{im}}}\frac{\boldsymbol{{cos}}\left(\boldsymbol{{sinx}}^{\mathrm{2}} \right)−\mathrm{1}}{\boldsymbol{{x}}^{\mathrm{2}} }\:=\:\underset{\boldsymbol{{X}}\rightarrow\mathrm{0}} {\boldsymbol{{lim}}}\frac{\boldsymbol{{cos}}\left(\boldsymbol{{sinX}}\right)−\boldsymbol{{cos}}\left(\boldsymbol{{sin}}\mathrm{0}\right)}{\boldsymbol{{X}}−\mathrm{0}}\:=\:\boldsymbol{{cos}}\left(\boldsymbol{{sinX}}\right)\right]'_{\left(\boldsymbol{{X}}=\mathrm{0}\right)} \:=\:−\boldsymbol{{cosXsin}}\left(\boldsymbol{{sinX}}\right)\right]_{\left(\boldsymbol{{X}}=\mathrm{0}\right)} \:=\:\mathrm{0} \\ $$
