
Question Number 70008 by Shamim last updated on 30/Sep/19
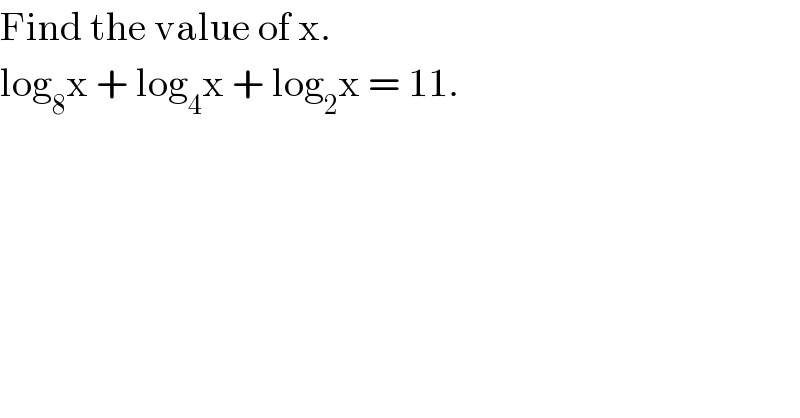
$$\mathrm{Find}\:\mathrm{the}\:\mathrm{value}\:\mathrm{of}\:\mathrm{x}. \\ $$$$\mathrm{log}_{\mathrm{8}} \mathrm{x}\:+\:\mathrm{log}_{\mathrm{4}} \mathrm{x}\:+\:\mathrm{log}_{\mathrm{2}} \mathrm{x}\:=\:\mathrm{11}. \\ $$
Answered by Maclaurin Stickker last updated on 30/Sep/19
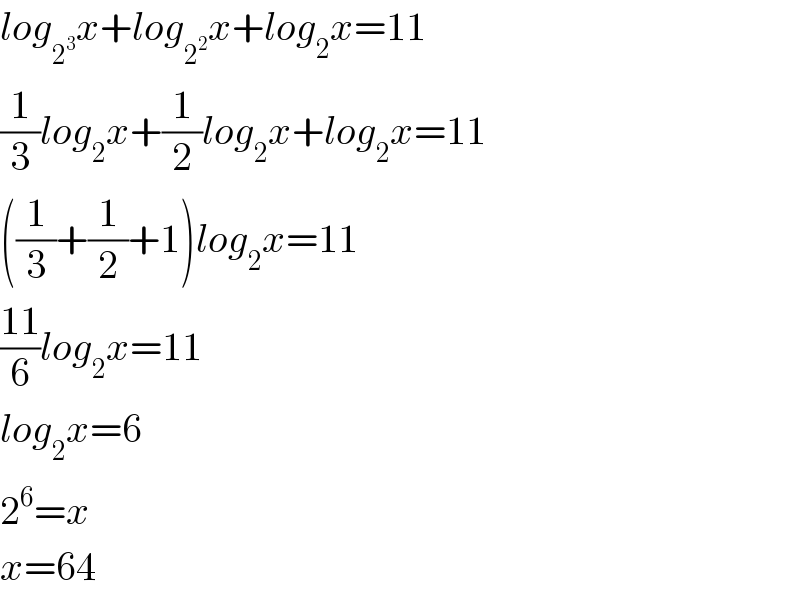
$${log}_{\mathrm{2}^{\mathrm{3}} } {x}+{log}_{\mathrm{2}^{\mathrm{2}} } {x}+{log}_{\mathrm{2}} {x}=\mathrm{11} \\ $$$$\frac{\mathrm{1}}{\mathrm{3}}{log}_{\mathrm{2}} {x}+\frac{\mathrm{1}}{\mathrm{2}}{log}_{\mathrm{2}} {x}+{log}_{\mathrm{2}} {x}=\mathrm{11} \\ $$$$\left(\frac{\mathrm{1}}{\mathrm{3}}+\frac{\mathrm{1}}{\mathrm{2}}+\mathrm{1}\right){log}_{\mathrm{2}} {x}=\mathrm{11} \\ $$$$\frac{\mathrm{11}}{\mathrm{6}}{log}_{\mathrm{2}} {x}=\mathrm{11} \\ $$$${log}_{\mathrm{2}} {x}=\mathrm{6} \\ $$$$\mathrm{2}^{\mathrm{6}} ={x} \\ $$$${x}=\mathrm{64} \\ $$
Commented by Shamim last updated on 30/Sep/19

$$\mathrm{tnks}\:\mathrm{a}\:\mathrm{lot}. \\ $$
Commented by Shamim last updated on 30/Sep/19

$$\mathrm{plz}\:\mathrm{explain}\:\mathrm{with}\:\mathrm{details}- \\ $$$$\mathrm{log}_{\mathrm{2}^{\mathrm{3}} } \mathrm{x}=\frac{\mathrm{1}}{\mathrm{3}}\mathrm{log}_{\mathrm{2}} \mathrm{x} \\ $$$$\mathrm{which}\:\mathrm{law}\:\mathrm{use}\:\mathrm{for}\:\mathrm{this}?? \\ $$
Commented by Tony Lin last updated on 30/Sep/19
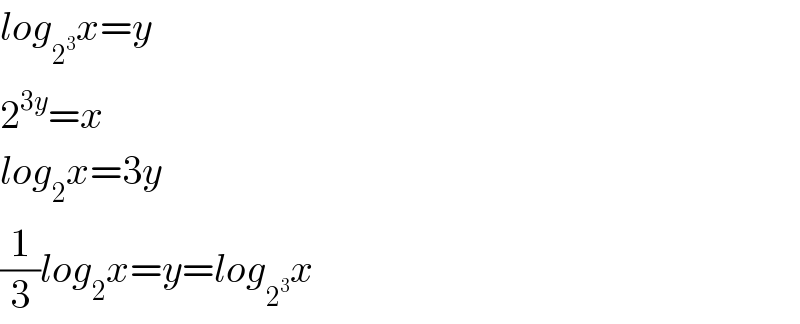
$${log}_{\mathrm{2}^{\mathrm{3}} } {x}={y} \\ $$$$\mathrm{2}^{\mathrm{3}{y}} ={x} \\ $$$${log}_{\mathrm{2}} {x}=\mathrm{3}{y} \\ $$$$\frac{\mathrm{1}}{\mathrm{3}}{log}_{\mathrm{2}} {x}={y}={log}_{\mathrm{2}^{\mathrm{3}} } {x} \\ $$
