
Question Number 70003 by Maclaurin Stickker last updated on 29/Sep/19
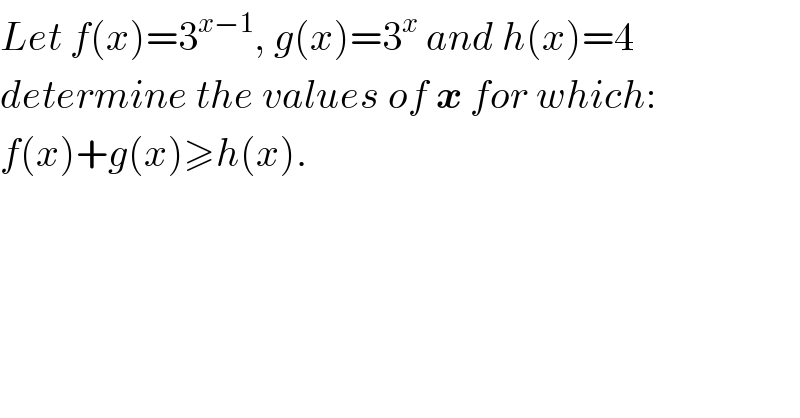
$${Let}\:{f}\left({x}\right)=\mathrm{3}^{{x}−\mathrm{1}} ,\:{g}\left({x}\right)=\mathrm{3}^{{x}} \:{and}\:{h}\left({x}\right)=\mathrm{4} \\ $$$${determine}\:{the}\:{values}\:{of}\:\boldsymbol{{x}}\:{for}\:{which}: \\ $$$${f}\left({x}\right)+{g}\left({x}\right)\geqslant{h}\left({x}\right). \\ $$$$ \\ $$
Commented by Abdo msup. last updated on 30/Sep/19
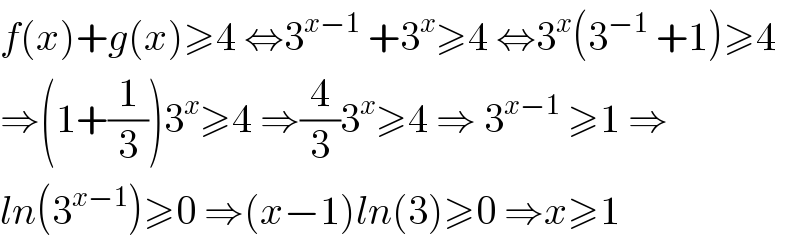
$${f}\left({x}\right)+{g}\left({x}\right)\geqslant\mathrm{4}\:\Leftrightarrow\mathrm{3}^{{x}−\mathrm{1}} \:+\mathrm{3}^{{x}} \geqslant\mathrm{4}\:\Leftrightarrow\mathrm{3}^{{x}} \left(\mathrm{3}^{−\mathrm{1}} \:+\mathrm{1}\right)\geqslant\mathrm{4} \\ $$$$\Rightarrow\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{3}}\right)\mathrm{3}^{{x}} \geqslant\mathrm{4}\:\Rightarrow\frac{\mathrm{4}}{\mathrm{3}}\mathrm{3}^{{x}} \geqslant\mathrm{4}\:\Rightarrow\:\mathrm{3}^{{x}−\mathrm{1}} \:\geqslant\mathrm{1}\:\Rightarrow \\ $$$${ln}\left(\mathrm{3}^{{x}−\mathrm{1}} \right)\geqslant\mathrm{0}\:\Rightarrow\left({x}−\mathrm{1}\right){ln}\left(\mathrm{3}\right)\geqslant\mathrm{0}\:\Rightarrow{x}\geqslant\mathrm{1} \\ $$
Commented by Maclaurin Stickker last updated on 30/Sep/19

$${Perfect}. \\ $$
Commented by Abdo msup. last updated on 11/Oct/19

$${thankx} \\ $$
