Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 85441 by jagoll last updated on 22/Mar/20

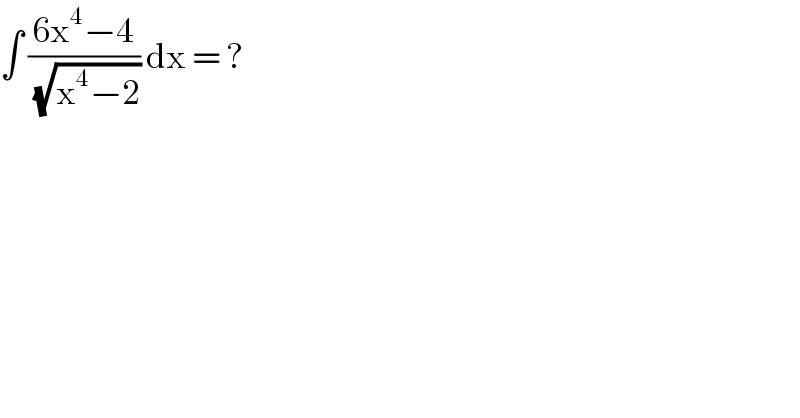
∫ ((6x^4 −4)/(√(x^4 −2))) dx = ?

$$\int\:\frac{\mathrm{6x}^{\mathrm{4}} −\mathrm{4}}{\sqrt{\mathrm{x}^{\mathrm{4}} −\mathrm{2}}}\:\mathrm{dx}\:=\:? \\ $$

Answered by john santu last updated on 22/Mar/20

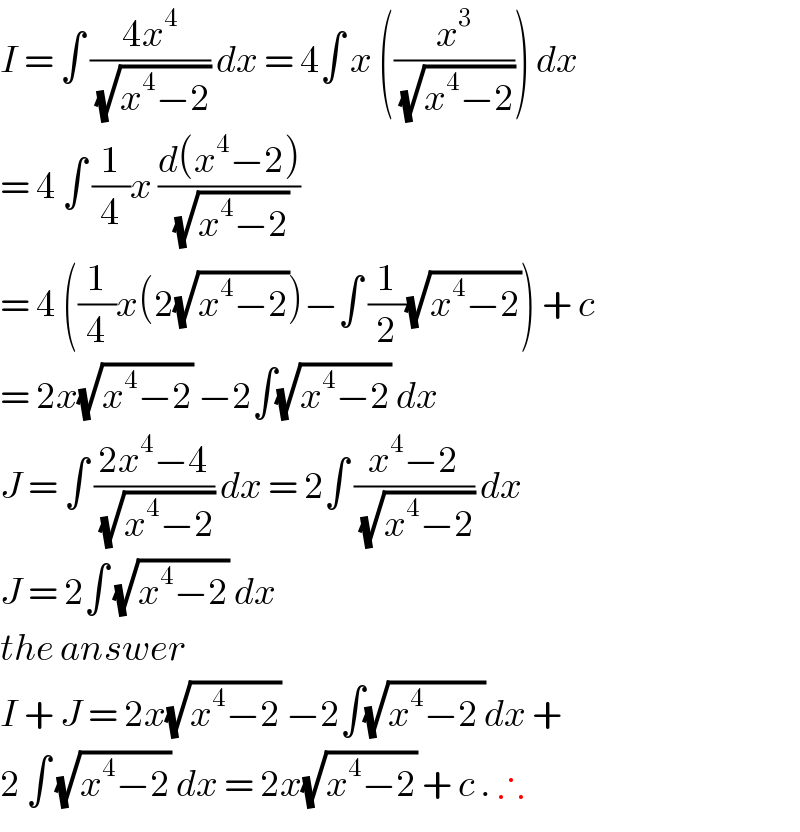
I = ∫ ((4x^4 )/(√(x^4 −2))) dx = 4∫ x ((x^3 /(√(x^4 −2)))) dx = 4 ∫ (1/4)x ((d(x^4 −2))/(√(x^4 −2))) = 4 ((1/4)x(2(√(x^4 −2)))−∫ (1/2)(√(x^4 −2))) + c = 2x(√(x^4 −2)) −2∫(√(x^4 −2)) dx J = ∫ ((2x^4 −4)/(√(x^4 −2))) dx = 2∫ ((x^4 −2)/(√(x^4 −2))) dx J = 2∫ (√(x^4 −2)) dx the answer I + J = 2x(√(x^4 −2)) −2∫(√(x^4 −2 ))dx + 2 ∫ (√(x^4 −2)) dx = 2x(√(x^4 −2)) + c . ∴

$${I}\:=\:\int\:\frac{\mathrm{4}{x}^{\mathrm{4}} }{\sqrt{{x}^{\mathrm{4}} −\mathrm{2}}}\:{dx}\:=\:\mathrm{4}\int\:{x}\:\left(\frac{{x}^{\mathrm{3}} }{\sqrt{{x}^{\mathrm{4}} −\mathrm{2}}}\right)\:{dx}\: \\ $$$$=\:\mathrm{4}\:\int\:\frac{\mathrm{1}}{\mathrm{4}}{x}\:\frac{{d}\left({x}^{\mathrm{4}} −\mathrm{2}\right)}{\sqrt{{x}^{\mathrm{4}} −\mathrm{2}}} \\ $$$$=\:\mathrm{4}\:\left(\frac{\mathrm{1}}{\mathrm{4}}{x}\left(\mathrm{2}\sqrt{{x}^{\mathrm{4}} −\mathrm{2}}\right)−\int\:\frac{\mathrm{1}}{\mathrm{2}}\sqrt{{x}^{\mathrm{4}} −\mathrm{2}}\right)\:+\:{c} \\ $$$$=\:\mathrm{2}{x}\sqrt{{x}^{\mathrm{4}} −\mathrm{2}}\:−\mathrm{2}\int\sqrt{{x}^{\mathrm{4}} −\mathrm{2}}\:{dx} \\ $$$${J}\:=\:\int\:\frac{\mathrm{2}{x}^{\mathrm{4}} −\mathrm{4}}{\sqrt{{x}^{\mathrm{4}} −\mathrm{2}}}\:{dx}\:=\:\mathrm{2}\int\:\frac{{x}^{\mathrm{4}} −\mathrm{2}}{\sqrt{{x}^{\mathrm{4}} −\mathrm{2}}}\:{dx} \\ $$$${J}\:=\:\mathrm{2}\int\:\sqrt{{x}^{\mathrm{4}} −\mathrm{2}}\:{dx} \\ $$$${the}\:{answer}\: \\ $$$${I}\:+\:{J}\:=\:\mathrm{2}{x}\sqrt{{x}^{\mathrm{4}} −\mathrm{2}}\:−\mathrm{2}\int\sqrt{{x}^{\mathrm{4}} −\mathrm{2}\:}{dx}\:+\: \\ $$$$\mathrm{2}\:\int\:\sqrt{{x}^{\mathrm{4}} −\mathrm{2}}\:{dx}\:=\:\mathrm{2}{x}\sqrt{{x}^{\mathrm{4}} −\mathrm{2}}\:+\:{c}\:.\:\therefore \\ $$

Commented by jagoll last updated on 22/Mar/20

thank you sir

$$\mathrm{thank}\:\mathrm{you}\:\mathrm{sir} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com