
Question Number 69939 by mr W last updated on 29/Sep/19
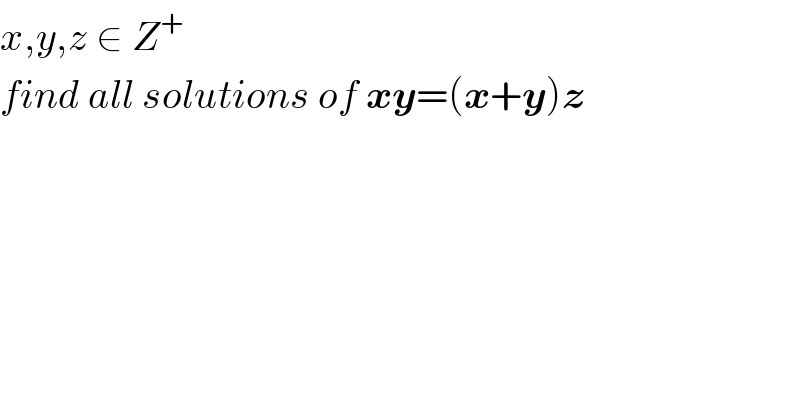
$${x},{y},{z}\:\in\:{Z}^{+} \\ $$$${find}\:{all}\:{solutions}\:{of}\:\boldsymbol{{xy}}=\left(\boldsymbol{{x}}+\boldsymbol{{y}}\right)\boldsymbol{{z}} \\ $$
Commented by Rasheed.Sindhi last updated on 29/Sep/19

$${k}\in\mathbb{Z}^{+} \:{in}\:{the}\:{following}. \\ $$$$\left({x},{y},{z}\right)=\left(\mathrm{2}{k},\mathrm{2}{k},{k}\right), \\ $$$$\left(\mathrm{5}{k},\mathrm{20}{k},\mathrm{4}{k}\right),\left(\mathrm{20}{k},\mathrm{5}{k},\mathrm{4}{k}\right), \\ $$$$\left(\mathrm{3}{k},\mathrm{6}{k},\mathrm{2}{k}\right),\left(\mathrm{6}{k},\mathrm{3}{k},\mathrm{2}{k}\right),\left(\mathrm{7}{k},\mathrm{42}{k},\mathrm{6}{k}\right), \\ $$$$\left(\mathrm{4},\mathrm{12},\mathrm{3}\right) \\ $$$$\:^{\bullet\:} {If}\:\left({p},{q},{r}\right)\:{is}\:{a}\:{solution}\:{then}\:\left({q},{p},{r}\right) \\ $$$$\:\:{is}\:{also}\:{solution}. \\ $$$$\:^{\bullet} \:{If}\:\left({p},{q},{r}\right)\:{is}\:{a}\:{solution}\:{then}\:\left({pk},{qk},{rk}\right) \\ $$$$\:\:\:\:{is}\:{also}\:{solution}.{k}\in\mathbb{Z}^{+} \\ $$$$.... \\ $$
Commented by mr W last updated on 29/Sep/19

$${thanks}\:{sir}! \\ $$$${these}\:{are}\:{solutions}.\:{but}\:{how}\:{can}\:{we}\: \\ $$$${express}\:{ALL}\:{possible}\:{solutions}? \\ $$
Commented by Rasheed.Sindhi last updated on 29/Sep/19

$${Sir}\:{at}\:{the}\:{moment}\:{I}\:{have}\:{no}\:{idea}\:{of} \\ $$$${expressing}\:{all}\:{the}\:{possible}\:{solutions}! \\ $$$${However}\:{I}\:{am}\:{thinking}\:{about}\:{it}... \\ $$
Commented by mr W last updated on 29/Sep/19
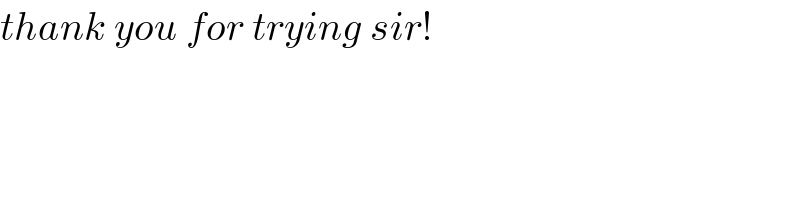
$${thank}\:{you}\:{for}\:{trying}\:{sir}! \\ $$
Commented by Rasheed.Sindhi last updated on 29/Sep/19

$${Sir}\:{I}\:{think}\:{infinite}\:{solutions}! \\ $$$${I}'{ll}\:{try}\:{to}\:{write}\:{some}\:{observations} \\ $$$${about}\:{such}\:{triplets}\:{which}\:{satisfy} \\ $$$${your}\:{equation}. \\ $$
Commented by mind is power last updated on 29/Sep/19

$${suppose}\:{x}\:{and}\:{y}\:{coprime} \\ $$$$\Rightarrow{x}+{y}\:{and}\:{xy}\:{are}\:{coprim}\: \\ $$$$\Rightarrow{xy}\mid{z}\Rightarrow{z}={xy}\:{and}\:{x}+{y}=\mathrm{1} \\ $$$${now}\:{assume}\:{x}\:{and}\:{y}\:{are}\:{note}\:{coprim} \\ $$$${let}\:{d}={gcd}\left({x},{y}\right)\Rightarrow{x}={dx}',{y}={dy}' \\ $$$${x}',{y}'\:{coprime} \\ $$$$\Rightarrow{d}^{\mathrm{2}} {x}'{y}'={d}\left({x}'+{y}'\right){z} \\ $$$$\Rightarrow{dx}'{y}'=\left({x}'+{y}'\right){z} \\ $$$${x}'{y}'\mid{z}\:\:{cause}\:{x}'+{y}'\:{and}\:{x}'{y}'\:{are}\:{coprime}\: \\ $$$${and}\:{x}'{y}'\mid{dx}'{y}'=\left({x}'+{y}'\right){z} \\ $$$${z}={x}'{y}'.{k} \\ $$$$\Rightarrow{d}={k}\left({x}'+{y}'\right) \\ $$$${let}\:{S}=\left\{{n}\in\mathbb{N}\:\:\:{n}\mid{d}\right\} \\ $$$${for}\:{all}\:{m}\in\mathbb{N}^{\ast} \:{we}\:{can}\:{Whrite}\:{m}={p}+{q}\:{withe}\:{p},{q}\:{coprim}\:{m}=\mathrm{1}+\left({m}−\mathrm{1}\right) \\ $$$${k}={m}\:{withe}\:{m}\in{S} \\ $$$${x}'+{y}'=\frac{{d}}{{m}}\in{S} \\ $$$$\left({x}',{y}'\right)\in\left\{\left({a},{b}\right)\mid{a}+{b}=\frac{{d}}{{m}},{and}\:{gcd}\left({a},{b}\right)=\mathrm{1}\right\} \\ $$$${x}={dx}'={da} \\ $$$${y}={dx}'={db} \\ $$$${z}={kx}'{y}'={mab} \\ $$$$ \\ $$
Commented by Prithwish sen last updated on 30/Sep/19

$$ \\ $$$$\mathrm{Given} \\ $$$$\mathrm{xy}=\mathrm{xz}+\mathrm{yz} \\ $$$$\Rightarrow\:\mathrm{2xy}−\mathrm{2xz}−\mathrm{2yz}\:=\:\mathrm{0}\:......\left(\mathrm{i}\right) \\ $$$$\mathrm{and}\:\mathrm{2xy}+\mathrm{2xz}+\mathrm{2yz}=\left(\mathrm{x}+\mathrm{y}+\mathrm{z}\right)^{\mathrm{2}} −\left(\mathrm{x}^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} +\mathrm{z}^{\mathrm{2}} \right).....\left(\mathrm{ii}\right) \\ $$$$\mathrm{Adding}\:\left(\mathrm{i}\right)\:\mathrm{and}\:\left(\mathrm{ii}\right) \\ $$$$\Rightarrow\mathrm{xy}=\frac{\left(\mathrm{x}+\mathrm{y}+\mathrm{z}\right)^{\mathrm{2}} −\left(\mathrm{x}^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} +\mathrm{z}^{\mathrm{2}} \right)}{\mathrm{4}}\:.....\left(\mathrm{iii}\right) \\ $$$$\boldsymbol{\mathrm{Now}}\:\boldsymbol{\mathrm{there}}\:\boldsymbol{\mathrm{are}}\:\boldsymbol{\mathrm{three}}\:\boldsymbol{\mathrm{possibilities}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\boldsymbol{\mathrm{x}}\:\:\:\:\:\:\:\:\:\:\:\:\boldsymbol{\mathrm{y}}\:\:\:\:\:\:\:\:\:\:\:\boldsymbol{\mathrm{z}} \\ $$$$\boldsymbol{\mathrm{Case}}\:\boldsymbol{\mathrm{I}}\:\:\:\:\:\boldsymbol{\mathrm{even}}\:\:\:\:\:\:\boldsymbol{\mathrm{odd}}\:\:\:\:\:\boldsymbol{\mathrm{even}} \\ $$$$\boldsymbol{\mathrm{Case}}\:\boldsymbol{\mathrm{I}}\mathrm{I}\:\:\:\boldsymbol{\mathrm{even}}\:\:\:\:\:\:\:\:\boldsymbol{\mathrm{even}}\:\:\:\boldsymbol{\mathrm{odd}} \\ $$$$\boldsymbol{\mathrm{CaseIII}}\:\:\:\boldsymbol{\mathrm{even}}\:\:\:\:\:\boldsymbol{\mathrm{even}}\:\:\:\:\boldsymbol{\mathrm{even}} \\ $$$$\boldsymbol{\mathrm{Now}}\:\boldsymbol{\mathrm{here}}\:\boldsymbol{\mathrm{I}}\:\boldsymbol{\mathrm{am}}\:\boldsymbol{\mathrm{considering}}\:\boldsymbol{\mathrm{only}}\:\boldsymbol{\mathrm{Case}}\:\boldsymbol{\mathrm{I}}\: \\ $$$$\mathrm{Let}\:\mathrm{x}=\:\mathrm{2m}\:\:\mathrm{y}=\:\mathrm{2n}+\mathrm{1}\:\:\mathrm{z}\:=\:\mathrm{2p} \\ $$$$\:\:\:\:\:\Rightarrow\:\:\mathrm{p}\:=\:\frac{\mathrm{m}\left(\mathrm{2n}+\mathrm{1}\right)}{\mathrm{2}\left(\mathrm{m}+\mathrm{n}\right)+\mathrm{1}} \\ $$$$\Rightarrow\:\mathrm{2}\boldsymbol{\mathrm{mp}}+\mathrm{2}\boldsymbol{\mathrm{np}}+\boldsymbol{\mathrm{p}}\:=\:\mathrm{2}\boldsymbol{\mathrm{mn}}\:+\boldsymbol{\mathrm{m}}\:........\left(\boldsymbol{\mathrm{iv}}\right) \\ $$$$\mathrm{Now}\:\mathrm{from}\:\left(\mathrm{iii}\right) \\ $$$$\:\:\boldsymbol{\mathrm{xy}}\:=\:\frac{\left(\mathrm{2}\boldsymbol{\mathrm{m}}+\mathrm{2}\boldsymbol{\mathrm{n}}+\mathrm{2}\boldsymbol{\mathrm{p}}+\mathrm{1}\right)^{\mathrm{2}} −\left\{\mathrm{4}\boldsymbol{\mathrm{m}}^{\mathrm{2}} +\left(\mathrm{2}\boldsymbol{\mathrm{n}}+\mathrm{1}\right)^{\mathrm{2}} +\mathrm{4}\boldsymbol{\mathrm{p}}^{\mathrm{2}} \right\}}{\mathrm{4}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:=\:\frac{\mathrm{8}\boldsymbol{\mathrm{mn}}+\mathrm{8}\boldsymbol{\mathrm{mp}}+\mathrm{8}\boldsymbol{\mathrm{np}}+\mathrm{4}\boldsymbol{\mathrm{m}}+\mathrm{4}\boldsymbol{\mathrm{p}}}{\mathrm{4}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:=\left(\:\mathrm{2}\boldsymbol{\mathrm{mp}}+\mathrm{2}\boldsymbol{\mathrm{np}}+\boldsymbol{\mathrm{p}}\right)+\mathrm{2}\boldsymbol{\mathrm{mn}}+\boldsymbol{\mathrm{m}}\:=\:\mathrm{4}\boldsymbol{\mathrm{mn}}\:+\mathrm{2}\boldsymbol{\mathrm{m}} \\ $$$$\:\:\:\mathrm{Now}\:\because\:\boldsymbol{\mathrm{p}}\:\boldsymbol{\mathrm{is}}\:\boldsymbol{\mathrm{an}}\:\boldsymbol{\mathrm{integer}} \\ $$$$\therefore\:\mathrm{p}\:=\:\mathrm{n}+\:\frac{\mathrm{m}−\mathrm{2n}^{\mathrm{2}} −\mathrm{n}}{\mathrm{2m}+\mathrm{2n}+\mathrm{1}} \\ $$$$\Rightarrow\mathrm{m}−\mathrm{2n}^{\mathrm{2}} −\mathrm{n}=\mathrm{0} \\ $$$$\Rightarrow\:\boldsymbol{\mathrm{n}}\:=\:\frac{\sqrt{\mathrm{1}+\mathrm{8}\boldsymbol{\mathrm{m}}}−\mathrm{1}}{\mathrm{4}}\:\:=\:\frac{\left(\mathrm{1}+\mathrm{4}\boldsymbol{\mathrm{q}}\right)−\mathrm{1}}{\mathrm{4}}\:=\:\boldsymbol{\mathrm{q}}\:\:\boldsymbol{\mathrm{putting}}\:\:\boldsymbol{\mathrm{m}}\:=\:\mathrm{2}\boldsymbol{\mathrm{q}}^{\mathrm{2}} +\boldsymbol{\mathrm{q}} \\ $$$$\mathrm{p}\:=\frac{\left(\mathrm{2}\boldsymbol{\mathrm{q}}^{\mathrm{2}} +\boldsymbol{\mathrm{q}}\right)\left(\mathrm{2}\boldsymbol{\mathrm{q}}+\mathrm{1}\right)}{\mathrm{2}\left\{\left(\mathrm{2}\boldsymbol{\mathrm{q}}^{\mathrm{2}} +\boldsymbol{\mathrm{q}}\right)+\boldsymbol{\mathrm{q}}\right\}+\mathrm{1}}\:=\:\frac{\boldsymbol{\mathrm{q}}\left(\mathrm{2}\boldsymbol{\mathrm{q}}+\mathrm{1}\right)^{\mathrm{2}} }{\mathrm{2}\boldsymbol{\mathrm{q}}\left(\mathrm{2}\boldsymbol{\mathrm{q}}+\mathrm{1}\right)+\mathrm{2}\boldsymbol{\mathrm{q}}+\mathrm{1}} \\ $$$$\:\:=\boldsymbol{\mathrm{q}} \\ $$$$\therefore\:\boldsymbol{\mathrm{x}}\:=\:\mathrm{2}\boldsymbol{\mathrm{q}}\left(\mathrm{2}\boldsymbol{\mathrm{q}}+\mathrm{1}\right)\:,\:\boldsymbol{\mathrm{y}}\:=\mathrm{2}\boldsymbol{\mathrm{q}}+\mathrm{1}\:\boldsymbol{\mathrm{and}}\:\boldsymbol{\mathrm{z}}\:=\:\mathrm{2}\boldsymbol{\mathrm{q}} \\ $$$$\:\:\:\:\:\:\:\boldsymbol{\mathrm{q}}\:\:\:\:\:\:\:\:\boldsymbol{\mathrm{x}}\:\:\:\:\:\:\:\:\:\:\:\boldsymbol{\mathrm{y}}\:\:\:\:\:\:\:\boldsymbol{\mathrm{z}} \\ $$$$\:\:\:\:\:\:\:\:\:\mathrm{1}\:\:\:\:\:\:\:\mathrm{6}\:\:\:\:\:\:\:\:\:\:\mathrm{3}\:\:\:\:\:\:\:\mathrm{2} \\ $$$$\:\:\:\:\:\:\:\:\:\mathrm{2}\:\:\:\:\:\:\mathrm{20}\:\:\:\:\:\:\:\:\:\mathrm{5}\:\:\:\:\:\:\:\:\mathrm{4} \\ $$$$\:\:\:\:\:\:\:\:\:\mathrm{3}\:\:\:\:\:\:\mathrm{42}\:\:\:\:\:\:\:\:\:\mathrm{7}\:\:\:\:\:\:\:\:\mathrm{6} \\ $$$$\:\:\:\:\:\:\:\:\:\:\mathrm{4}\:\:\:\:\:\:\mathrm{72}\:\:\:\:\:\:\:\:\mathrm{9}\:\:\:\:\:\:\:\mathrm{8} \\ $$$$\:\:\:\:\:\:\:\boldsymbol{\mathrm{and}}\:\boldsymbol{\mathrm{so}}\:\boldsymbol{\mathrm{on}}\:......... \\ $$$$\boldsymbol{\mathrm{m}},\boldsymbol{\mathrm{n}},\boldsymbol{\mathrm{p}}\:,\boldsymbol{\mathrm{q}}\:\boldsymbol{\mathrm{are}}\:\boldsymbol{\mathrm{integers}} \\ $$$$\boldsymbol{\mathrm{Mr}}.\:\boldsymbol{\mathrm{W}}\:\boldsymbol{\mathrm{Sir}}\:\boldsymbol{\mathrm{and}}\:\boldsymbol{\mathrm{Rasheed}}\:\boldsymbol{\mathrm{Sir}}\:\boldsymbol{\mathrm{please}}\:\boldsymbol{\mathrm{give}}\:\boldsymbol{\mathrm{your}} \\ $$$$\boldsymbol{\mathrm{valuable}}\:\boldsymbol{\mathrm{suggestions}}.\boldsymbol{\mathrm{Sir}}\:\boldsymbol{\mathrm{I}}\:\:\boldsymbol{\mathrm{make}}\:\boldsymbol{\mathrm{the}}\:\boldsymbol{\mathrm{whole}}\:\boldsymbol{\mathrm{thing}}\: \\ $$$$\boldsymbol{\mathrm{only}}\:\boldsymbol{\mathrm{dependent}}\:\boldsymbol{\mathrm{on}}\:\boldsymbol{\mathrm{q}}.\:\boldsymbol{\mathrm{By}}\:\boldsymbol{\mathrm{putting}}\:\boldsymbol{\mathrm{q}}=\mathrm{1},\mathrm{2},... \\ $$$$\boldsymbol{\mathrm{and}}\:\boldsymbol{\mathrm{you}}\:\boldsymbol{\mathrm{get}}\:\boldsymbol{\mathrm{the}}\:\boldsymbol{\mathrm{result}}. \\ $$
Commented by mr W last updated on 29/Sep/19
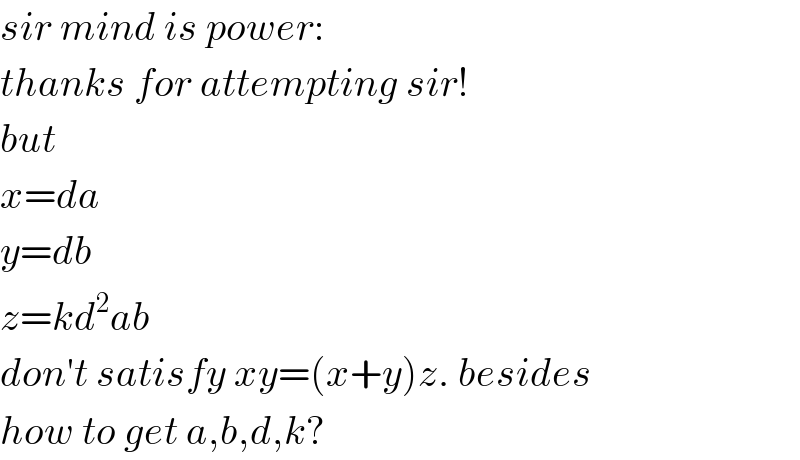
$${sir}\:{mind}\:{is}\:{power}: \\ $$$${thanks}\:{for}\:{attempting}\:{sir}! \\ $$$${but} \\ $$$${x}={da} \\ $$$${y}={db} \\ $$$${z}={kd}^{\mathrm{2}} {ab} \\ $$$${don}'{t}\:{satisfy}\:{xy}=\left({x}+{y}\right){z}.\:{besides} \\ $$$${how}\:{to}\:{get}\:{a},{b},{d},{k}? \\ $$
Commented by mind is power last updated on 29/Sep/19
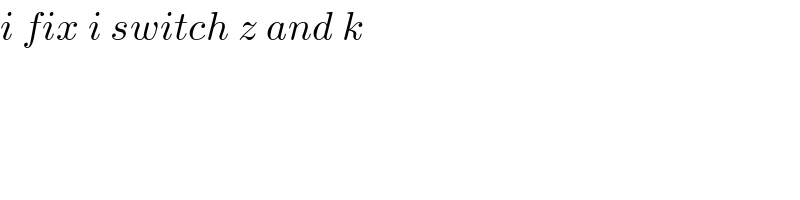
$${i}\:{fix}\:{i}\:{switch}\:{z}\:{and}\:{k}\: \\ $$
Commented by mr W last updated on 29/Sep/19
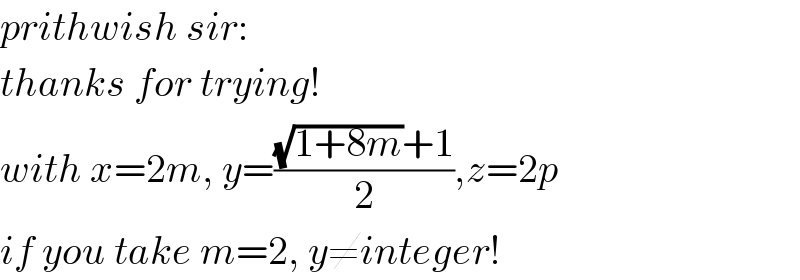
$${prithwish}\:{sir}: \\ $$$${thanks}\:{for}\:{trying}! \\ $$$${with}\:{x}=\mathrm{2}{m},\:{y}=\frac{\sqrt{\mathrm{1}+\mathrm{8}{m}}+\mathrm{1}}{\mathrm{2}},{z}=\mathrm{2}{p} \\ $$$${if}\:{you}\:{take}\:{m}=\mathrm{2},\:{y}\neq{integer}! \\ $$
Commented by mr W last updated on 29/Sep/19

$${there}\:{are}\:{three}\:{unknowns}\:{x},{y},{z}. \\ $$$${a}\:{general}\:{solution}\:{must}\:{have}\:{two} \\ $$$${parameters}\:{in}\:{the}\:{expression}.\:{this} \\ $$$${is}\:{like}\:{to}\:{find}\:{the}\:{general}\:{integer} \\ $$$${solution}\:{for}\:{x}+\mathrm{2}{y}+{z}=\mathrm{7}. \\ $$
Commented by mind is power last updated on 29/Sep/19

$${d}\:{given}\:{parameter} \\ $$$${z}={dab} \\ $$$${m}\:{divusor}\:{of}\:{d}\: \\ $$$${a}\:{and}\:{b}\:{are}\:{such}\:{a}+{b}=\frac{{d}}{{m}} \\ $$$${and}\:{gcd}\left({a},{b}\right)=\mathrm{1} \\ $$$${a}=\frac{{d}}{{m}}−{b} \\ $$$${gcd}\left({a},{b}\right)=\mathrm{1}\Rightarrow{gcd}\left(\frac{{d}}{{m}},{b}\right) \\ $$$${soit}\:{b}\:{is}\:{coprime}\:{withe}\:\frac{{d}}{{m}\:}\:{withe}\:{b}\leqslant\frac{{d}}{{m}} \\ $$$${same}\:{withe}\:{a}\:{coprime}\:{withe}\:\frac{{d}}{{m}} \\ $$$$\left({a},{b}\right)\ast{describe}\:{all}\:{integer}\:{withe}\:{a}+{b}=\frac{{d}}{{m}}\:{withe}\:{a}\:{and}\:{b}\:{coprime}\:{withe}\:\frac{{d}}{{m}} \\ $$$${exampl}\:{a}+{b}=\mathrm{6} \\ $$$$\left({a},{b}\right)\in\left\{\left(\mathrm{1},\mathrm{5}\right)\:\left(\mathrm{5},\mathrm{1}\right)\right\} \\ $$$${Sorry}\:{my}\:{english}\:{not}\:{Good} \\ $$$$ \\ $$$$ \\ $$
Answered by Rasheed.Sindhi last updated on 02/Oct/19

$${I}\:{have}\:{made}\:{a}\:{formula}\:{which}\:{produce} \\ $$$${a}\:{triplet}\:{satisfying}\:{the}\:{given}\:{equation} \\ $$$${for}\:{every}\:{pair}\:{of}\:{positive}\:{integers}: \\ $$$$\:{Let}\:{p},{q}\in\mathbb{Z}^{+} \\ $$$${x}={p}\left({p}+{q}\right) \\ $$$${y}={q}\left({p}+{q}\right) \\ $$$${z}={pq} \\ $$$${We}\:{can}\:{algebraically}\:{prove}\:{that} \\ $$$$\left({x},{y},{z}\right)=\left(\:{p}\left({p}+{q}\right)\:,\:{q}\left({p}+{q}\right)\:,\:{pq}\:\right)\:{is}\:{solution} \\ $$$${of}\:\:\boldsymbol{{xy}}=\left(\boldsymbol{{x}}+\boldsymbol{{y}}\right)\boldsymbol{{z}} \\ $$$${This}\:{proves}\:{that}\:{the}\:{solutions}\:{are} \\ $$$${infinite}. \\ $$$$\boldsymbol{{Claim}}: \\ $$$$\:^{\bullet} {If}\:\:{p}\:\&\:{q}\:{be}\:{coprime}\:{then} \\ $$$$\left({x},{y},{z}\right)\:{will}\:{be}\:{primitive}\:{triple}\:{satisfying} \\ $$$${xy}=\left({x}+{y}\right){z} \\ $$$$\:^{\bullet} {The}\:{above}\:{formulas}\:{can}\:{produce} \\ $$$$\:\:{all}\:{the}\:{possible}\:{primitive}\:{solutions} \\ $$$$\:^{\bullet} {Non}-{primitive}\:{solution}\:{are}\:{merely} \\ $$$$\:\:{integral}\:{multiples}\:{of}\:{primitive}\:{solutions}. \\ $$$$ \\ $$$$\:\:\:{Your}\:{offered}\:{example}\left(\:\left(\mathrm{8},\mathrm{24},\mathrm{6}\right)\right)\:{is} \\ $$$$\:\:\:\:{is}\:{non}-{primitive}\:{solution}\:{and}\:{its} \\ $$$$\:\:\:\:{corresponding}\:{primitive}\:{solution} \\ $$$$\:\:\:{is}\:\left(\mathrm{4},\mathrm{12},\mathrm{3}\right)\:{and}\:{this}\:{can}\:{be}\:{produced} \\ $$$$\:\:\:{by}\:{my}\:{formulas}\:\left({put}\:{p}=\mathrm{1},{q}=\mathrm{3}\right). \\ $$$${How}\:{do}\:{you}\:{see}\:{this}\:{claim}.{please} \\ $$$${give}\:{a}\:{counter}\:{example}\:{if}\:{you}\:{don}'{t} \\ $$$${agree}. \\ $$
Commented by Prithwish sen last updated on 30/Sep/19

$$\mathrm{As}\:\mathrm{a}\:\mathrm{whole} \\ $$$$\mathrm{for}\:\mathrm{the}\:\mathrm{expression}\: \\ $$$$\boldsymbol{\mathrm{xy}}=\left(\boldsymbol{\mathrm{x}}+\boldsymbol{\mathrm{y}}\right)\boldsymbol{\mathrm{z}}\:\:\:\:\boldsymbol{\mathrm{x}},\boldsymbol{\mathrm{y}},\boldsymbol{\mathrm{z}}\:\in\mathbb{Z}^{+} \\ $$$$\mathrm{we}\:\mathrm{have} \\ $$$$\boldsymbol{\mathrm{Case}}\:\boldsymbol{\mathrm{I}}\:\boldsymbol{\mathrm{x}}=\mathrm{2}\boldsymbol{\mathrm{q}}\left(\mathrm{2}\boldsymbol{\mathrm{q}}+\mathrm{1}\right)\:\:\boldsymbol{\mathrm{y}}\:=\:\left(\mathrm{2}\boldsymbol{\mathrm{q}}+\mathrm{1}\right)\:\:\boldsymbol{\mathrm{z}}=\mathrm{2}\boldsymbol{\mathrm{q}} \\ $$$$\boldsymbol{\mathrm{Case}}\:\boldsymbol{\mathrm{II}}\:\boldsymbol{\mathrm{x}}\:=\:\mathrm{2}\boldsymbol{\mathrm{q}}\:\:\:\:\:\boldsymbol{\mathrm{y}}\:=\:\mathrm{2}\boldsymbol{\mathrm{q}}\left(\mathrm{2}\boldsymbol{\mathrm{q}}−\mathrm{1}\right)\:\:\boldsymbol{\mathrm{z}}\:=\:\mathrm{2}\boldsymbol{\mathrm{q}}−\mathrm{1} \\ $$$$\boldsymbol{\mathrm{and}}\:\boldsymbol{\mathrm{for}}\:\boldsymbol{\mathrm{Case}}\:\boldsymbol{\mathrm{III}}\:\boldsymbol{\mathrm{no}}\:\boldsymbol{\mathrm{such}}\:\boldsymbol{\mathrm{expression}}\:\boldsymbol{\mathrm{found}}. \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\boldsymbol{\mathrm{x}}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\boldsymbol{\mathrm{y}}\:\:\:\:\:\:\:\:\:\:\:\:\boldsymbol{\mathrm{z}} \\ $$$$\boldsymbol{\mathrm{q}}=\mathrm{1}\:\:\:\:\:\:\:\:\:\:\:\mathrm{6}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{3}\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{2}\:\:\:\:−\boldsymbol{\mathrm{Case}}\:\boldsymbol{\mathrm{I}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{2}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{2}\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{1}−\boldsymbol{\mathrm{Case}}\:\boldsymbol{\mathrm{II}} \\ $$$$\boldsymbol{\mathrm{q}}=\mathrm{2}\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{20}\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{5}\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{4}\:\:−\:\boldsymbol{\mathrm{Case}}\:\boldsymbol{\mathrm{I}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{4}\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{12}\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{3}\:−\:\boldsymbol{\mathrm{Case}}\:\boldsymbol{\mathrm{II}}\:\:\:\left(\boldsymbol{\mathrm{value}}\:\boldsymbol{\mathrm{of}}\right. \\ $$$$\boldsymbol{\mathrm{q}}=\mathrm{3}\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{42}\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{7}\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{6}−\:\boldsymbol{\mathrm{Case}}\:\boldsymbol{\mathrm{I}}\:\:\:\:\:\:\:\boldsymbol{\mathrm{x}}\:\boldsymbol{\mathrm{and}}\:\boldsymbol{\mathrm{y}}\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{6}\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{30}\:\:\:\:\:\:\:\:\:\:\:\mathrm{5}\:−\:\boldsymbol{\mathrm{Case}}\:\boldsymbol{\mathrm{II}}\:\:\:\:\boldsymbol{\mathrm{can}}\:\boldsymbol{\mathrm{be}}\: \\ $$$$\left.\boldsymbol{\mathrm{q}}=\mathrm{4}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{72}\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{9}\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{8}\:−\:\boldsymbol{\mathrm{Case}}\:\boldsymbol{\mathrm{I}}\:\:\:\:\:\boldsymbol{\mathrm{altered}}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{8}\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{56}\:\:\:\:\:\:\:\:\:\:\:\mathrm{7}\:−\:\boldsymbol{\mathrm{Case}}\:\boldsymbol{\mathrm{II}} \\ $$$$\boldsymbol{\mathrm{and}}\:\boldsymbol{\mathrm{so}}\:\boldsymbol{\mathrm{on}}...... \\ $$$$\boldsymbol{\mathrm{It}}\:\boldsymbol{\mathrm{confirms}}\:\boldsymbol{\mathrm{that}}\:\boldsymbol{\mathrm{the}}\:\boldsymbol{\mathrm{expression}}\:\boldsymbol{\mathrm{has}}\:\boldsymbol{\mathrm{infinite}} \\ $$$$\boldsymbol{\mathrm{number}}\:\boldsymbol{\mathrm{of}}\:\boldsymbol{\mathrm{solutions}}\:. \\ $$
Commented by Rasheed.Sindhi last updated on 03/Oct/19

$${Sir}\:{how}\:{can}\:{we}\:{prove}\:{that}\:{the}\:{above} \\ $$$${formulas}\:{can}\:{produce}\:\boldsymbol{{all}}\:{possible} \\ $$$${solutions}? \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\& \\ $$$${What}'{s}\:{the}\:{sourse}\:{of}\:{problem}? \\ $$
Commented by mr W last updated on 29/Sep/19

$${that}'{s}\:{a}\:{nice}\:{way}\:{sir}! \\ $$$${from}\:{given}\:{p}\:{and}\:{q}\:{we}\:{can}\:{construct} \\ $$$${a}\:{solution}.\:{but}\:{there}\:{could}\:{be}\:{more} \\ $$$${than}\:{just}\:{one}\:{solution}\:{for}\:{given}\:{p},\:{q}. \\ $$$${e}.{g}.\:{z}=\mathrm{6} \\ $$$$\left({x},{y}\right)=\left(\mathrm{10},\mathrm{15}\right)\:{is}\:{a}\:{solution},{but} \\ $$$$\left(\mathrm{8},\mathrm{24}\right)\:{is}\:{also}\:{a}\:{solution}. \\ $$
Commented by Rasheed.Sindhi last updated on 30/Sep/19

$${Yes}\:{sir},{the}\:{formula}\:{doesn}'{t}\:{cover}\:{all} \\ $$$${possible}\:{solutions}.{However}\:{it}\:{assures} \\ $$$${that}\:{there}\:{are}\:{infinite}\:{solutions}. \\ $$$${For}\:{composite}\:{z},\:{the}\:{formula}\:{can} \\ $$$${give}\:{multiple}\:{solutions}.\:{For}\:{example} \\ $$$${z}=\mathrm{6}\Rightarrow{pq}=\mathrm{6}\Rightarrow\left({p},{q}\right)=\left(\mathrm{1},\mathrm{6}\right)\:{or}\:\left(\mathrm{2},\mathrm{3}\right) \\ $$$$\Rightarrow\left({x},\bar {{y}},{z}\right)=\left(\mathrm{7},\mathrm{42},\mathrm{6}\right)\:{or}\:\left(\mathrm{10},\mathrm{15},\mathrm{6}\right). \\ $$$${But}\:{afterall}\:{the}\:{formula}\:{doesn}'{t} \\ $$$${cover}\:{all}\:{possible}\:{solutions}. \\ $$
Commented by Prithwish sen last updated on 30/Sep/19

$$\mathrm{Mr}\:\mathrm{W}.\:\mathrm{Sir}\:\mathrm{please}\:\mathrm{see}\:\mathrm{my}\:\mathrm{solution}\:\mathrm{I}\:\mathrm{have}\: \\ $$$$\mathrm{fix}\:\mathrm{my}\:\mathrm{error}.\:\mathrm{I}\:\mathrm{think}\:\mathrm{I}\:\mathrm{get}\:\mathrm{a}\:\mathrm{general}\:\mathrm{formula}\:\: \\ $$$$\mathrm{with}\:\mathrm{a}\:\mathrm{single}\:\mathrm{parameter}\:\boldsymbol{\mathrm{q}}. \\ $$$$ \\ $$
Commented by Prithwish sen last updated on 30/Sep/19
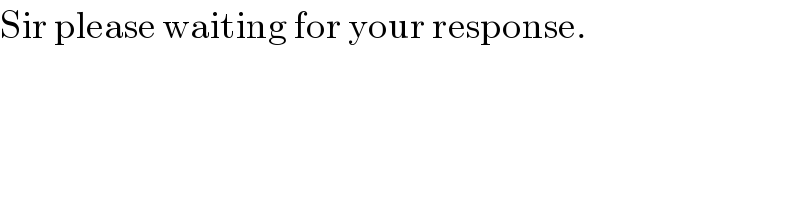
$$\mathrm{Sir}\:\mathrm{please}\:\mathrm{waiting}\:\mathrm{for}\:\mathrm{your}\:\mathrm{response}. \\ $$
Commented by mr W last updated on 30/Sep/19
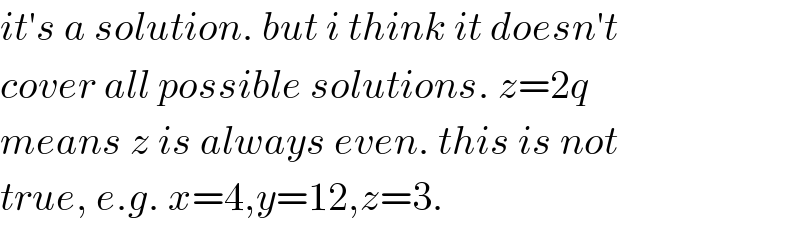
$${it}'{s}\:{a}\:{solution}.\:{but}\:{i}\:{think}\:{it}\:{doesn}'{t} \\ $$$${cover}\:{all}\:{possible}\:{solutions}.\:{z}=\mathrm{2}{q} \\ $$$${means}\:{z}\:{is}\:{always}\:{even}.\:{this}\:{is}\:{not} \\ $$$${true},\:{e}.{g}.\:{x}=\mathrm{4},{y}=\mathrm{12},{z}=\mathrm{3}. \\ $$
Commented by Rasheed.Sindhi last updated on 30/Sep/19

$${Prithwish}\:{sen}\:{sir} \\ $$$${Your}\:'{product}\:{machine}'\:{is}\:{wonderful}! \\ $$$${It}\:{produces}\:{solutions}\:{successfully}. \\ $$$${But}\:{there}\:{are}\:{some}\:{solutions}\:{which} \\ $$$${can}'{t}\:{be}\:{produced}\:{by}\:{your}\:{machine}. \\ $$$${Whereas}\:{mr}\:{W}\:{sir}\:{demands}\:{such} \\ $$$${machine}\:{which}\:{can}\:{produce}\:{all}\:{possible} \\ $$$${solutions}! \\ $$$${For}\:{example}\:{for}\:{z}=\mathrm{6}\:{your}\:{machine} \\ $$$$\left({farmula}\right)\:{produces}\:{single}\:{triplet} \\ $$$$\left({solution}\right):\left(\mathrm{42},\mathrm{7},\mathrm{6}\right)\:{by}\:{putting}\:{q}=\mathrm{3}. \\ $$$${Whereas}\:{many}\:{other}\:{triplets}\left({which}\right. \\ $$$$\left.{aren}'{t}\:{come}\:{from}\:{your}\:{machine}\right) \\ $$$${satisfy}\:{the}\:{equation}\:\boldsymbol{{xy}}=\left(\boldsymbol{{x}}+\boldsymbol{{y}}\right)\boldsymbol{{z}}. \\ $$$${Such}\:{as}\:\left(\mathrm{10},\mathrm{15},\mathrm{6}\right)\:{etc}\:\left({Can}\:{this}\:{be}\right. \\ $$$$\left.{produced}\:{by}\:{your}\:{formula}?\right) \\ $$
Commented by Prithwish sen last updated on 30/Sep/19

$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{sir}. \\ $$
Commented by mr W last updated on 30/Sep/19

$${thank}\:{you}\:{all}\:{sirs}! \\ $$
Commented by Prithwish sen last updated on 01/Oct/19

$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{sir}. \\ $$$$ \\ $$
Commented by Rasheed.Sindhi last updated on 01/Oct/19

$${An}\:\mathcal{E}{quivalent}\:\mathcal{E}{xpression}\:{of}\: \\ $$$$\boldsymbol{{xy}}=\left(\boldsymbol{{x}}+\boldsymbol{{y}}\right)\boldsymbol{{z}}. \\ $$$$\boldsymbol{{xy}}=\left(\boldsymbol{{x}}+\boldsymbol{{y}}\right)\boldsymbol{{z}}\Rightarrow\boldsymbol{{xy}}−\boldsymbol{{yz}}−\boldsymbol{{zx}}=\mathrm{0} \\ $$$$\Rightarrow\boldsymbol{{xy}}+\boldsymbol{{y}}\left(−\boldsymbol{{z}}\right)+\left(−\boldsymbol{{z}}\right)\boldsymbol{{x}}=\mathrm{0} \\ $$$${Now}, \\ $$$$\:\left(\boldsymbol{{x}}+\boldsymbol{{y}}−\boldsymbol{{z}}\right)^{\mathrm{2}} =\boldsymbol{{x}}^{\mathrm{2}} +\boldsymbol{{y}}^{\mathrm{2}} +\boldsymbol{{z}}^{\mathrm{2}} +\mathrm{2}\left(\boldsymbol{{xy}}+\boldsymbol{{y}}\left(−\boldsymbol{{z}}\right)+\left(−\boldsymbol{{z}}\right)\boldsymbol{{x}}\right) \\ $$$$\:\:\:\:\:\:\:=\boldsymbol{{x}}^{\mathrm{2}} +\boldsymbol{{y}}^{\mathrm{2}} +\boldsymbol{{z}}^{\mathrm{2}} +\mathrm{2}\left(\mathrm{0}\right) \\ $$$$\boldsymbol{{x}}^{\mathrm{2}} +\boldsymbol{{y}}^{\mathrm{2}} +\boldsymbol{{z}}^{\mathrm{2}} =\left(\boldsymbol{{x}}+\boldsymbol{{y}}−\boldsymbol{{z}}\right)^{\mathrm{2}} \\ $$$$\boldsymbol{{This}}\:\boldsymbol{{is}}\:\boldsymbol{{equivalent}}\:\boldsymbol{{to}}\:\boldsymbol{{xy}}=\left(\boldsymbol{{x}}+\boldsymbol{{y}}\right)\boldsymbol{{z}} \\ $$$$\boldsymbol{{i}}-\boldsymbol{{e}}\:\boldsymbol{{solutions}}\:\boldsymbol{{of}}\:\boldsymbol{{both}}\:\boldsymbol{{are}}\:\boldsymbol{{same}}. \\ $$$${Note}:{The}\:{idea}\:{raised}\:{in}\:{my}\:{mind}\:{after} \\ $$$${seeing}\:{a}\:{comment}\:{of}\:{Prithwish}\:{sen}\:{sir}. \\ $$
Commented by Rasheed.Sindhi last updated on 03/Oct/19
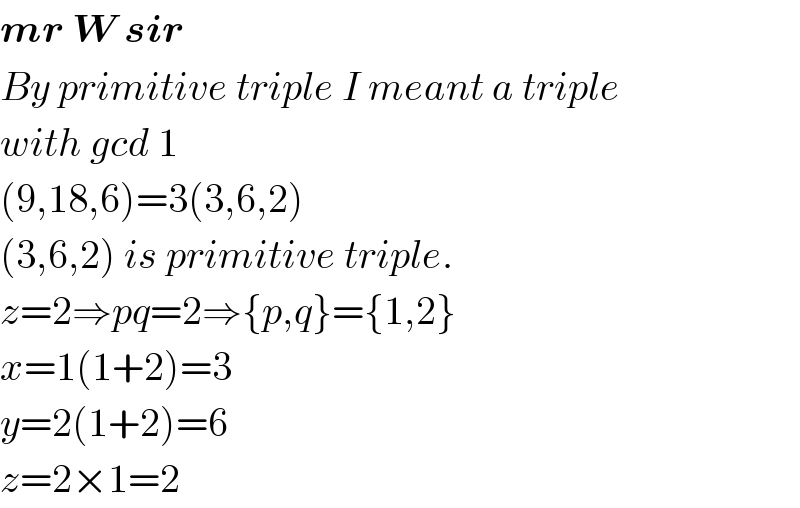
$$\boldsymbol{{mr}}\:\boldsymbol{{W}}\:\boldsymbol{{sir}} \\ $$$${By}\:{primitive}\:{triple}\:{I}\:{meant}\:{a}\:{triple} \\ $$$${with}\:{gcd}\:\mathrm{1} \\ $$$$\left(\mathrm{9},\mathrm{18},\mathrm{6}\right)=\mathrm{3}\left(\mathrm{3},\mathrm{6},\mathrm{2}\right) \\ $$$$\left(\mathrm{3},\mathrm{6},\mathrm{2}\right)\:{is}\:{primitive}\:{triple}. \\ $$$${z}=\mathrm{2}\Rightarrow{pq}=\mathrm{2}\Rightarrow\left\{{p},{q}\right\}=\left\{\mathrm{1},\mathrm{2}\right\} \\ $$$${x}=\mathrm{1}\left(\mathrm{1}+\mathrm{2}\right)=\mathrm{3} \\ $$$${y}=\mathrm{2}\left(\mathrm{1}+\mathrm{2}\right)=\mathrm{6} \\ $$$${z}=\mathrm{2}×\mathrm{1}=\mathrm{2} \\ $$
Commented by mr W last updated on 03/Oct/19
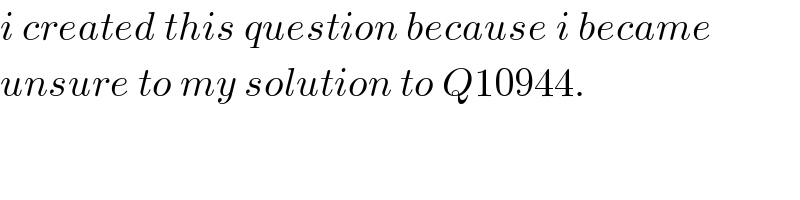
$${i}\:{created}\:{this}\:{question}\:{because}\:{i}\:{became} \\ $$$${unsure}\:{to}\:{my}\:{solution}\:{to}\:{Q}\mathrm{10944}. \\ $$
Commented by Rasheed.Sindhi last updated on 02/Oct/19
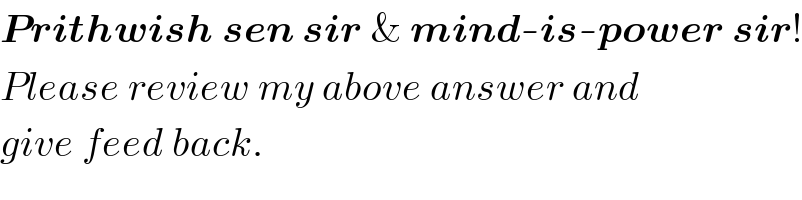
$$\boldsymbol{{Prithwish}}\:\boldsymbol{{sen}}\:\boldsymbol{{sir}}\:\&\:\boldsymbol{{mind}}-\boldsymbol{{is}}-\boldsymbol{{power}}\:\boldsymbol{{sir}}! \\ $$$${Please}\:{review}\:{my}\:{above}\:{answer}\:{and} \\ $$$${give}\:{feed}\:{back}. \\ $$
Commented by Rasheed.Sindhi last updated on 02/Oct/19

$$\boldsymbol{{Sir}}\:\boldsymbol{{mr}}\:\boldsymbol{{W}} \\ $$$${Please}\:{review}\:{my}\:{above}\:{answer}.{I}'{ve} \\ $$$${added}\:{some}\:{material}\:{in}\:{red}\:{lines}\:. \\ $$$${I}'{m}\:{anxiously}\:{waiting}\:{for}\:{your}\:{response}. \\ $$
Commented by mr W last updated on 02/Oct/19
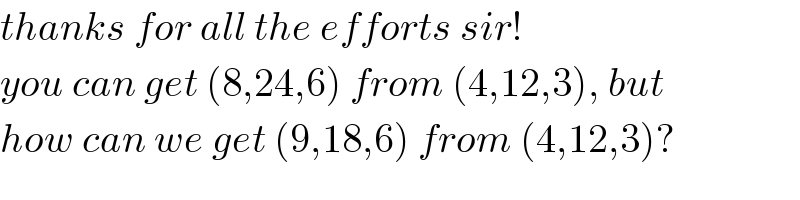
$${thanks}\:{for}\:{all}\:{the}\:{efforts}\:{sir}! \\ $$$${you}\:{can}\:{get}\:\left(\mathrm{8},\mathrm{24},\mathrm{6}\right)\:{from}\:\left(\mathrm{4},\mathrm{12},\mathrm{3}\right),\:{but} \\ $$$${how}\:{can}\:{we}\:{get}\:\left(\mathrm{9},\mathrm{18},\mathrm{6}\right)\:{from}\:\left(\mathrm{4},\mathrm{12},\mathrm{3}\right)? \\ $$
Commented by mr W last updated on 03/Oct/19

$${now}\:{i}\:{see}.\:{thanks}\:{sir}! \\ $$$${the}\:{task}\:{is}\:{now}\:{how}\:{to}\:{express}\:{x}\:{and}\:{y} \\ $$$${x}={f}\left({p},{q}\right) \\ $$$${y}={g}\left({p},{q}\right) \\ $$$${z}={pq} \\ $$$${such}\:{that}\:{x}\:{and}\:{y}\:{cover}\:{all}\:{possibilities}. \\ $$$${can}\:{we}\:{find}\:{the}\:{f}\left({p},{q}\right)\:{and}\:{g}\left({p},{q}\right)? \\ $$
Commented by Rasheed.Sindhi last updated on 03/Oct/19

$${x}={f}\left({p},{q}\right)={p}\left({p}+{q}\right) \\ $$$${y}={g}\left({p},{q}\right)={q}\left({p}+{q}\right) \\ $$$${z}={h}\left({p},{q}\right)={pq} \\ $$$${For}\:{a}\:{given}\:{z}=\mathrm{12}\left({say}\right) \\ $$$${z}=\mathrm{12}\Rightarrow{pq}=\mathrm{12}\:\left({for}\:{primitive}\:{solutions}\right. \\ $$$$\left.{take}\:{p}\:\&\:{q}\:{coprime}\right) \\ $$$$\left({p},{q}\right)=\:\left(\mathrm{1},\mathrm{12}\right),\left(\mathrm{3},\mathrm{4}\right),\left(\mathrm{4},\mathrm{3}\right),\left(\mathrm{12},\mathrm{1}\right) \\ $$$$\left(\mathrm{1},\mathrm{12}\right):\:{x}=\mathrm{1}\left(\mathrm{1}+\mathrm{12}\right)=\mathrm{13} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{y}=\mathrm{12}\left(\mathrm{1}+\mathrm{12}\right)=\mathrm{156} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{z}=\mathrm{12} \\ $$$${All}\:{possible}\:{primitive}\:{solutions}\:{with} \\ $$$${z}=\mathrm{12}\:{are}:\:\left(\mathrm{13},\mathrm{156},\mathrm{12}\right),\left(\mathrm{21},\mathrm{28},\mathrm{12}\right), \\ $$$$\left(\mathrm{28},\mathrm{21},\mathrm{12}\right)\:\&\:\left(\mathrm{156},\mathrm{13},\mathrm{12}\right) \\ $$$${For}\:{primitive}\:{solutions}\:{with}\:{z}=\mathrm{12} \\ $$$${x}\:\&\:{y}\:{can}'{t}\:{take}\:{other}\:{values}\: \\ $$$$\left({If}\:{my}\:{claim}\:{is}\:{right}\right).{If}\:{x}\:\&\:{y}\:{have} \\ $$$${values}\:{other}\:{than}\:{above},\:{then}\:{the} \\ $$$${that}\:{solution}\:{must}\:{be}\:{non}-{primitive}. \\ $$$${please}\:{try}\:{counter}\:{example}:\left({a},{b},\mathrm{12}\right) \\ $$$${such}\:{that}\:{gcd}\left({a},{b},\mathrm{12}\right)=\mathrm{1}\:{and}\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{ab}=\mathrm{12}\left({a}+{b}\right) \\ $$
Commented by mr W last updated on 03/Oct/19
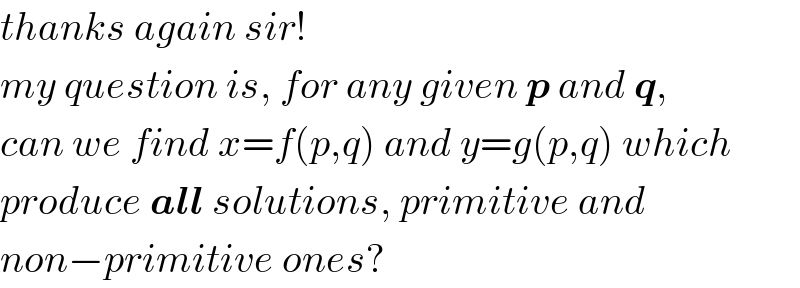
$${thanks}\:{again}\:{sir}! \\ $$$${my}\:{question}\:{is},\:{for}\:{any}\:{given}\:\boldsymbol{{p}}\:{and}\:\boldsymbol{{q}}, \\ $$$${can}\:{we}\:{find}\:{x}={f}\left({p},{q}\right)\:{and}\:{y}={g}\left({p},{q}\right)\:{which} \\ $$$${produce}\:\boldsymbol{{all}}\:{solutions},\:{primitive}\:{and} \\ $$$${non}−{primitive}\:{ones}? \\ $$
Commented by Rasheed.Sindhi last updated on 03/Oct/19

$${By}\:{adding}\:{one}\:{additional}\:{parameter}\:{k}: \\ $$$${x}={kp}\left({p}+{q}\right) \\ $$$${y}={kq}\left({p}+{q}\right) \\ $$$${z}={kpq} \\ $$$${p}\:\&\:{q}\:{being}\:{coprime}\:{and}\:{k}\:{any}\:{positive} \\ $$$${integer}.\:{I}\:{think}\:{sir}\:{these}\:{formulas} \\ $$$${can}\:{cover}\:\boldsymbol{{all}}\:{primitive}\:{as}\:{well}\:{as} \\ $$$${non}-{primitive}\:{solutions}. \\ $$
Commented by mr W last updated on 03/Oct/19

$${big}\:{big}\:{thanks}\:{sir}! \\ $$
Answered by Rasheed.Sindhi last updated on 02/Oct/19
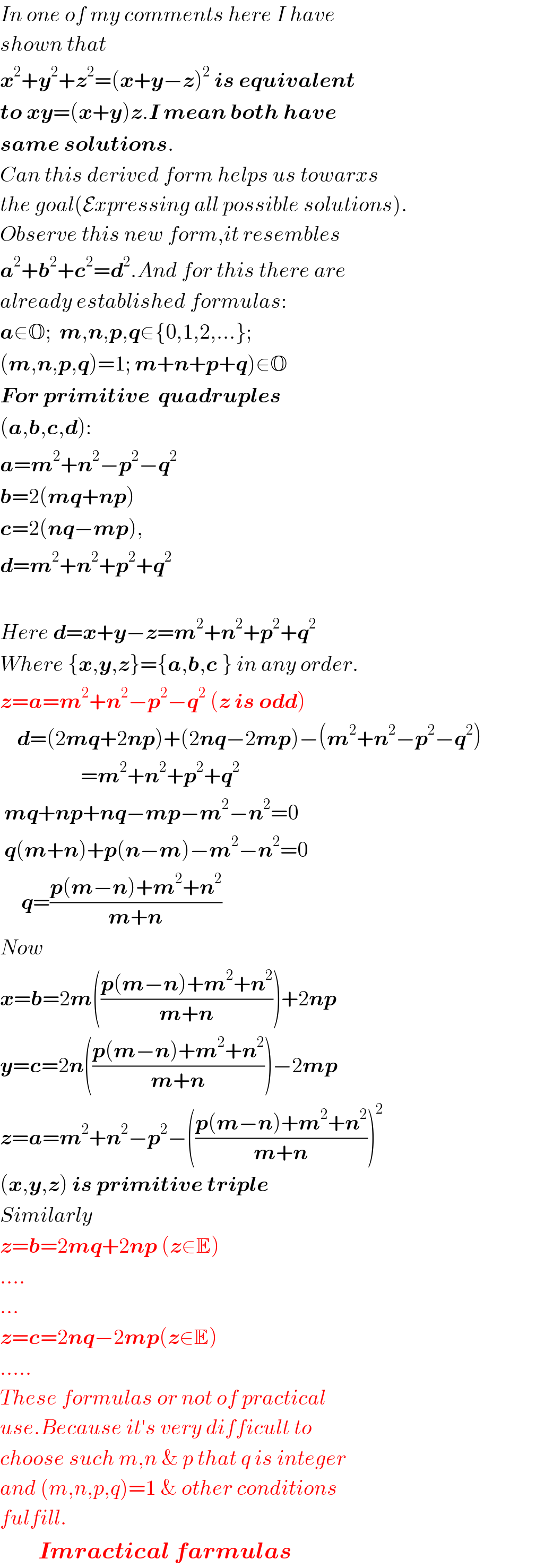
$${In}\:{one}\:{of}\:{my}\:{comments}\:{here}\:{I}\:{have} \\ $$$${shown}\:{that}\: \\ $$$$\boldsymbol{{x}}^{\mathrm{2}} +\boldsymbol{{y}}^{\mathrm{2}} +\boldsymbol{{z}}^{\mathrm{2}} =\left(\boldsymbol{{x}}+\boldsymbol{{y}}−\boldsymbol{{z}}\right)^{\mathrm{2}} \:\boldsymbol{{is}}\:\boldsymbol{{equivalent}} \\ $$$$\boldsymbol{{to}}\:\boldsymbol{{xy}}=\left(\boldsymbol{{x}}+\boldsymbol{{y}}\right)\boldsymbol{{z}}.\boldsymbol{{I}}\:\boldsymbol{{mean}}\:\boldsymbol{{both}}\:\boldsymbol{{have}} \\ $$$$\boldsymbol{{same}}\:\boldsymbol{{solutions}}. \\ $$$${Can}\:{this}\:{derived}\:{form}\:{helps}\:{us}\:{towarxs} \\ $$$${the}\:{goal}\left(\mathcal{E}{xpressing}\:{all}\:{possible}\:{solutions}\right). \\ $$$${Observe}\:{this}\:{new}\:{form},{it}\:{resembles} \\ $$$$\boldsymbol{{a}}^{\mathrm{2}} +\boldsymbol{{b}}^{\mathrm{2}} +\boldsymbol{{c}}^{\mathrm{2}} =\boldsymbol{{d}}^{\mathrm{2}} .{And}\:{for}\:{this}\:{there}\:{are} \\ $$$${already}\:{established}\:{formulas}: \\ $$$$\boldsymbol{{a}}\in\mathbb{O};\:\:\boldsymbol{{m}},\boldsymbol{{n}},\boldsymbol{{p}},\boldsymbol{{q}}\in\left\{\mathrm{0},\mathrm{1},\mathrm{2},...\right\}; \\ $$$$\left.\left(\boldsymbol{{m}},\boldsymbol{{n}},\boldsymbol{{p}},\boldsymbol{{q}}\right)=\mathrm{1};\:\boldsymbol{{m}}+\boldsymbol{{n}}+\boldsymbol{{p}}+\boldsymbol{{q}}\right)\in\mathbb{O} \\ $$$$\boldsymbol{{For}}\:\boldsymbol{{primitive}}\:\:\boldsymbol{{quadruples}}\: \\ $$$$\left(\boldsymbol{{a}},\boldsymbol{{b}},\boldsymbol{{c}},\boldsymbol{{d}}\right): \\ $$$$\boldsymbol{{a}}=\boldsymbol{{m}}^{\mathrm{2}} +\boldsymbol{{n}}^{\mathrm{2}} −\boldsymbol{{p}}^{\mathrm{2}} −\boldsymbol{{q}}^{\mathrm{2}} \\ $$$$\boldsymbol{{b}}=\mathrm{2}\left(\boldsymbol{{mq}}+\boldsymbol{{np}}\right) \\ $$$$\boldsymbol{{c}}=\mathrm{2}\left(\boldsymbol{{nq}}−\boldsymbol{{mp}}\right), \\ $$$$\boldsymbol{{d}}=\boldsymbol{{m}}^{\mathrm{2}} +\boldsymbol{{n}}^{\mathrm{2}} +\boldsymbol{{p}}^{\mathrm{2}} +\boldsymbol{{q}}^{\mathrm{2}} \\ $$$$ \\ $$$${Here}\:\boldsymbol{{d}}=\boldsymbol{{x}}+\boldsymbol{{y}}−\boldsymbol{{z}}=\boldsymbol{{m}}^{\mathrm{2}} +\boldsymbol{{n}}^{\mathrm{2}} +\boldsymbol{{p}}^{\mathrm{2}} +\boldsymbol{{q}}^{\mathrm{2}} \\ $$$${Where}\:\left\{\boldsymbol{{x}},\boldsymbol{{y}},\boldsymbol{{z}}\right\}=\left\{\boldsymbol{{a}},\boldsymbol{{b}},\boldsymbol{{c}}\:\right\}\:{in}\:{any}\:{order}. \\ $$$$\boldsymbol{{z}}=\boldsymbol{{a}}=\boldsymbol{{m}}^{\mathrm{2}} +\boldsymbol{{n}}^{\mathrm{2}} −\boldsymbol{{p}}^{\mathrm{2}} −\boldsymbol{{q}}^{\mathrm{2}} \:\left(\boldsymbol{{z}}\:\boldsymbol{{is}}\:\boldsymbol{{odd}}\right) \\ $$$$\:\:\:\:\boldsymbol{{d}}=\left(\mathrm{2}\boldsymbol{{mq}}+\mathrm{2}\boldsymbol{{np}}\right)+\left(\mathrm{2}\boldsymbol{{nq}}−\mathrm{2}\boldsymbol{{mp}}\right)−\left(\boldsymbol{{m}}^{\mathrm{2}} +\boldsymbol{{n}}^{\mathrm{2}} −\boldsymbol{{p}}^{\mathrm{2}} −\boldsymbol{{q}}^{\mathrm{2}} \right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\boldsymbol{{m}}^{\mathrm{2}} +\boldsymbol{{n}}^{\mathrm{2}} +\boldsymbol{{p}}^{\mathrm{2}} +\boldsymbol{{q}}^{\mathrm{2}} \\ $$$$\:\boldsymbol{{mq}}+\boldsymbol{{np}}+\boldsymbol{{nq}}−\boldsymbol{{mp}}−\boldsymbol{{m}}^{\mathrm{2}} −\boldsymbol{{n}}^{\mathrm{2}} =\mathrm{0} \\ $$$$\:\boldsymbol{{q}}\left(\boldsymbol{{m}}+\boldsymbol{{n}}\right)+\boldsymbol{{p}}\left(\boldsymbol{{n}}−\boldsymbol{{m}}\right)−\boldsymbol{{m}}^{\mathrm{2}} −\boldsymbol{{n}}^{\mathrm{2}} =\mathrm{0} \\ $$$$\:\:\:\:\:\boldsymbol{{q}}=\frac{\boldsymbol{{p}}\left(\boldsymbol{{m}}−\boldsymbol{{n}}\right)+\boldsymbol{{m}}^{\mathrm{2}} +\boldsymbol{{n}}^{\mathrm{2}} }{\boldsymbol{{m}}+\boldsymbol{{n}}} \\ $$$${Now} \\ $$$$\boldsymbol{{x}}=\boldsymbol{{b}}=\mathrm{2}\boldsymbol{{m}}\left(\frac{\boldsymbol{{p}}\left(\boldsymbol{{m}}−\boldsymbol{{n}}\right)+\boldsymbol{{m}}^{\mathrm{2}} +\boldsymbol{{n}}^{\mathrm{2}} }{\boldsymbol{{m}}+\boldsymbol{{n}}}\right)+\mathrm{2}\boldsymbol{{np}} \\ $$$$\boldsymbol{{y}}=\boldsymbol{{c}}=\mathrm{2}\boldsymbol{{n}}\left(\frac{\boldsymbol{{p}}\left(\boldsymbol{{m}}−\boldsymbol{{n}}\right)+\boldsymbol{{m}}^{\mathrm{2}} +\boldsymbol{{n}}^{\mathrm{2}} }{\boldsymbol{{m}}+\boldsymbol{{n}}}\right)−\mathrm{2}\boldsymbol{{mp}} \\ $$$$\boldsymbol{{z}}=\boldsymbol{{a}}=\boldsymbol{{m}}^{\mathrm{2}} +\boldsymbol{{n}}^{\mathrm{2}} −\boldsymbol{{p}}^{\mathrm{2}} −\left(\frac{\boldsymbol{{p}}\left(\boldsymbol{{m}}−\boldsymbol{{n}}\right)+\boldsymbol{{m}}^{\mathrm{2}} +\boldsymbol{{n}}^{\mathrm{2}} }{\boldsymbol{{m}}+\boldsymbol{{n}}}\right)^{\mathrm{2}} \:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\: \\ $$$$\left(\boldsymbol{{x}},\boldsymbol{{y}},\boldsymbol{{z}}\right)\:\boldsymbol{{is}}\:\boldsymbol{{primitive}}\:\boldsymbol{{triple}} \\ $$$${Similarly} \\ $$$$\boldsymbol{{z}}=\boldsymbol{{b}}=\mathrm{2}\boldsymbol{{mq}}+\mathrm{2}\boldsymbol{{np}}\:\left(\boldsymbol{{z}}\in\mathbb{E}\right) \\ $$$$.... \\ $$$$... \\ $$$$\boldsymbol{{z}}=\boldsymbol{{c}}=\mathrm{2}\boldsymbol{{nq}}−\mathrm{2}\boldsymbol{{mp}}\left(\boldsymbol{{z}}\in\mathbb{E}\right) \\ $$$$..... \\ $$$${These}\:{formulas}\:{or}\:{not}\:{of}\:{practical} \\ $$$${use}.{Because}\:{it}'{s}\:{very}\:{difficult}\:{to} \\ $$$${choose}\:{such}\:{m},{n}\:\&\:{p}\:{that}\:{q}\:{is}\:{integer} \\ $$$${and}\:\left({m},{n},{p},{q}\right)=\mathrm{1}\:\&\:{other}\:{conditions} \\ $$$${fulfill}. \\ $$$$\:\:\:\:\:\:\:\:\:\boldsymbol{{Imractical}}\:\boldsymbol{{farmulas}} \\ $$
Commented by Rasheed.Sindhi last updated on 01/Oct/19

$${I}\:{hope}\:{these}\:{formulas}\:{cover}\:{all}\: \\ $$$${possible}\:{primitive}\:{solutions}.{Non}- \\ $$$${primitive}\:{solutions}\:{are}\:{integral}\: \\ $$$${multiple}\:{of}\:{primitive}\:{solutions}. \\ $$
Commented by Prithwish sen last updated on 01/Oct/19

$$\mathrm{Sir}\:\mathrm{the}\:\mathrm{primitive}\:\mathrm{quadruples}\:\mathrm{which}\:\mathrm{you}\: \\ $$$$\mathrm{derived}\:\mathrm{from}\:\mathrm{the}\:\mathrm{lebesgue}'\mathrm{s}\:\mathrm{identity}.\:\mathrm{Are}\: \\ $$$$\mathrm{you}\:\mathrm{sure}\:\mathrm{that}\:\mathrm{it}\:\mathrm{covers}\:\mathrm{all}\:\mathrm{the}\:\mathrm{possible}\: \\ $$$$\mathrm{primitive}\:\mathrm{quadruples}\:?\: \\ $$
Commented by Prithwish sen last updated on 01/Oct/19

$$\mathrm{I}\:\mathrm{think}\:\mathrm{these}\:\mathrm{are}\:\mathrm{the}\:\mathrm{nessecary}\:\mathrm{but}\:\mathrm{not}\:\mathrm{the} \\ $$$$\mathrm{sufficient}\:\mathrm{condition}. \\ $$
Commented by Rasheed.Sindhi last updated on 01/Oct/19

Commented by Rasheed.Sindhi last updated on 01/Oct/19

$$``{Thus},\:{all}\:{primitivePythagorean}\:{quadruplesu} \\ $$$${are}\:{characterized}\:{by}\:{Lebsgue}'{s}\:{identity}...'' \\ $$$${Sir}\:{I}\:{meant}\:{by}\:{above}\:{that}\:{all}\:{possible} \\ $$$${primitive}\:{roots}\:{can}\:{be}\:{derived}.{May}\:{be} \\ $$$${I}\:{am}\:{wrong}. \\ $$
Commented by Prithwish sen last updated on 01/Oct/19

$$\mathrm{Actually}\:\mathrm{sir}\:\mathrm{I}\:\mathrm{have}\:\mathrm{some}\:\mathrm{doubt}\:\mathrm{to}\:\mathrm{clear}.\:\mathrm{By}\: \\ $$$$\mathrm{the}\:\mathrm{way}\:\mathrm{you}\:\mathrm{have}\:\mathrm{done}\:\mathrm{an}\:\mathrm{outstanding}\:\mathrm{work}. \\ $$$$\mathrm{Excellent}\:\mathrm{thinking}. \\ $$
Commented by Rasheed.Sindhi last updated on 03/Oct/19

$$\mathcal{THANKS}\:{in}\:{advance}\:{sir}!\:{My}\:{email} \\ $$$$\:{is}\:{below}: \\ $$$$\:\:\:\boldsymbol{{rasheedsindhi}}@\boldsymbol{{yahoo}}.\boldsymbol{{com}} \\ $$
Commented by Prithwish sen last updated on 03/Oct/19

$$\mathrm{Sir}\:\mathrm{I}\:\mathrm{have}\:\mathrm{already}\:\mathrm{sentyou}\:\mathrm{the}\:\mathrm{pdf}.\:\mathrm{If}\:\mathrm{you}\: \\ $$$$\mathrm{received}\:\mathrm{that}\:\mathrm{please}\:\mathrm{give}\:\mathrm{a}\:\mathrm{feedback}. \\ $$
Commented by Prithwish sen last updated on 03/Oct/19

$$\mathrm{Sir}\:\mathrm{actually}\:\mathrm{I}\:\mathrm{find}\:\mathrm{something}\:\mathrm{on}\:\mathrm{net}\:\mathrm{regarding} \\ $$$$\mathrm{pythagorean}\:\mathrm{quadruples}\:\mathrm{very}\:\mathrm{interesting}.\:\mathrm{I}\:\mathrm{will}\:\mathrm{post}\:\mathrm{it}\:\mathrm{later}.\: \\ $$$$\mathrm{Now}\:\mathrm{I}\:\mathrm{am}\:\mathrm{little}\:\mathrm{busy}.\:\mathrm{So}\:\mathrm{please}\:\mathrm{wait}. \\ $$
Commented by Prithwish sen last updated on 03/Oct/19

Commented by Prithwish sen last updated on 03/Oct/19

Commented by Prithwish sen last updated on 03/Oct/19

Commented by Rasheed.Sindhi last updated on 03/Oct/19

$$\mathcal{T}{h}\alpha{n}\mathcal{X}\:{Prithwish}\:{sen}\:{sir}\:{for}\:{this} \\ $$$${precious}\:{information}!\:{pl}\:{share}\:{web} \\ $$$${url}\:{also}! \\ $$
Commented by Prithwish sen last updated on 03/Oct/19

$$\mathrm{Sir}\:\mathrm{I}\:\mathrm{am}\:\mathrm{not}\:\mathrm{so}\:\mathrm{good}\:\mathrm{at}\:\mathrm{using}\:\mathrm{gadgets}.\:\mathrm{If}\:\mathrm{you} \\ $$$$\mathrm{send}\:\mathrm{your}\:\mathrm{mail}\:\mathrm{then}\:\mathrm{I}\:\mathrm{can}\:\mathrm{send}\:\mathrm{you}\:\mathrm{the}\:\mathrm{entire} \\ $$$$\mathrm{pdf}. \\ $$
Commented by Rasheed.Sindhi last updated on 03/Oct/19

$${Sir}\:{I}\:{recieved}\:{the}\:{pdf}.{I}'{ll}\:{study}\:{it}. \\ $$$${Thanks}\:{again}.{We}\:{should}\:{think}\:{how} \\ $$$${can}\:{we}\:{relate}\:{pythagoren}\:{quadruples} \\ $$$${to}\:{the}\:{question}\:{above}.{My}\:{attempt}\:{in} \\ $$$${this}\:{connection}\:{nearly}\:{failed}... \\ $$$$\:{Pl}\:{sir}\:{study}\:{my}\:{first}\:{answer}\:{again}. \\ $$$${I}\:{think}\:{formulas}\:{there}\:{can}\:{be}\:{used} \\ $$$${to}\:{produce}\:{all}\:{possible}\:{solutions}\:{of} \\ $$$$\boldsymbol{{xy}}=\left(\boldsymbol{{x}}+\boldsymbol{{y}}\right)\boldsymbol{{z}} \\ $$
Commented by Prithwish sen last updated on 03/Oct/19

$$\mathrm{Excellent}\:\mathrm{work}\:\mathrm{sir}.\:\mathrm{If}\:\mathrm{all}\:\mathrm{the}\:\mathrm{possible}\: \\ $$$$\mathrm{primitive}\:\mathrm{solutions}\:\mathrm{can}\:\mathrm{be}\:\mathrm{produced}\:\mathrm{then} \\ $$$$\mathrm{the}\:\mathrm{all}\:\mathrm{non}\:\mathrm{primitive}\:\mathrm{solutions}\:\mathrm{also}\:\mathrm{can}\:\mathrm{be} \\ $$$$\mathrm{produced}.\:\mathrm{Great}\:\mathrm{work}\:\mathrm{Sir}. \\ $$
Commented by Rasheed.Sindhi last updated on 03/Oct/19
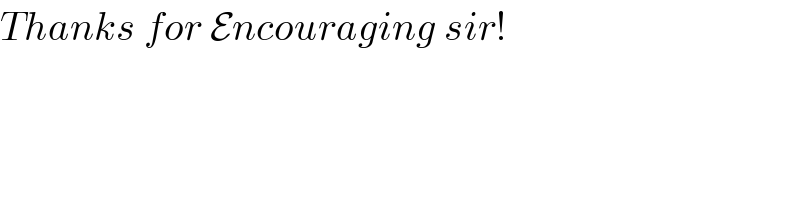
$${Thanks}\:{for}\:\mathcal{E}{ncouraging}\:{sir}! \\ $$
