
Question Number 69871 by Shamim last updated on 28/Sep/19
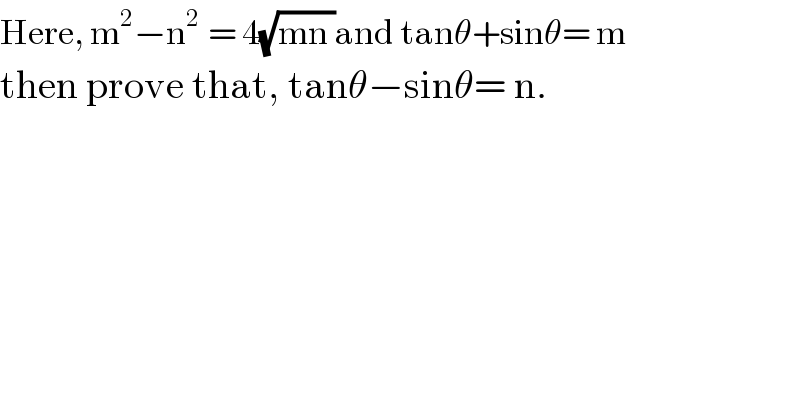
$$\mathrm{Here},\:\mathrm{m}^{\mathrm{2}} −\mathrm{n}^{\mathrm{2}\:\:} =\:\mathrm{4}\sqrt{\mathrm{mn}\:}\mathrm{and}\:\mathrm{tan}\theta+\mathrm{sin}\theta=\:\mathrm{m} \\ $$$$\mathrm{then}\:\mathrm{prove}\:\mathrm{that},\:\mathrm{tan}\theta−\mathrm{sin}\theta=\:\mathrm{n}. \\ $$
Answered by MJS last updated on 29/Sep/19

$$\mathrm{first}\:\mathrm{how}\:\mathrm{to}\:\mathrm{solve} \\ $$$${m}^{\mathrm{2}} −{n}^{\mathrm{2}} =\mathrm{4}\sqrt{{mn}} \\ $$$$\mathrm{for}\:{n} \\ $$$$\mathrm{squaring}\:\mathrm{is}\:\mathrm{a}\:\mathrm{bad}\:\mathrm{idea},\:\mathrm{it}\:\mathrm{leads}\:\mathrm{to} \\ $$$${n}^{\mathrm{4}} −\mathrm{2}{m}^{\mathrm{2}} {n}^{\mathrm{2}} −\mathrm{16}{mn}+{m}^{\mathrm{4}} =\mathrm{0} \\ $$$$\mathrm{and}\:\mathrm{it}'\mathrm{s}\:\mathrm{hard}\:\mathrm{to}\:\mathrm{solve} \\ $$$$\mathrm{instead}\:\mathrm{put}\:{m}={p}+{q},\:{n}={p}−{q} \\ $$$$\mathrm{4}{pq}=\mathrm{4}\sqrt{{p}^{\mathrm{2}} −{q}^{\mathrm{2}} } \\ $$$${p}^{\mathrm{2}} {q}^{\mathrm{2}} ={p}^{\mathrm{2}} −{q}^{\mathrm{2}} \\ $$$$\Rightarrow\:{q}=\pm\frac{{p}}{\sqrt{{p}^{\mathrm{2}} +\mathrm{1}}} \\ $$$$\Rightarrow\:{m}={p}\pm\frac{{p}}{\sqrt{{p}^{\mathrm{2}} +\mathrm{1}}},\:{n}={p}\mp\frac{{p}}{\sqrt{{p}^{\mathrm{2}} +\mathrm{1}}} \\ $$$$\mathrm{but}\:{m}=\mathrm{tan}\:\theta\:+\mathrm{sin}\:\theta \\ $$$$\mathrm{with}\:{p}=\mathrm{tan}\:\theta\:\mathrm{we}\:\mathrm{get}\:\frac{{p}}{\sqrt{{p}^{\mathrm{2}} +\mathrm{1}}}=\pm\mathrm{sin}\:\theta \\ $$$$\Rightarrow\:{n}=\mathrm{tan}\:\theta\:−\mathrm{sin}\:\theta \\ $$
Commented by $@ty@m123 last updated on 29/Sep/19

$${Wonderful}! \\ $$
Commented by Rasheed.Sindhi last updated on 29/Sep/19

$$\mathcal{X}{cellent}\:\mathcal{S}{ir}! \\ $$
