
Question Number 69778 by Rio Michael last updated on 27/Sep/19
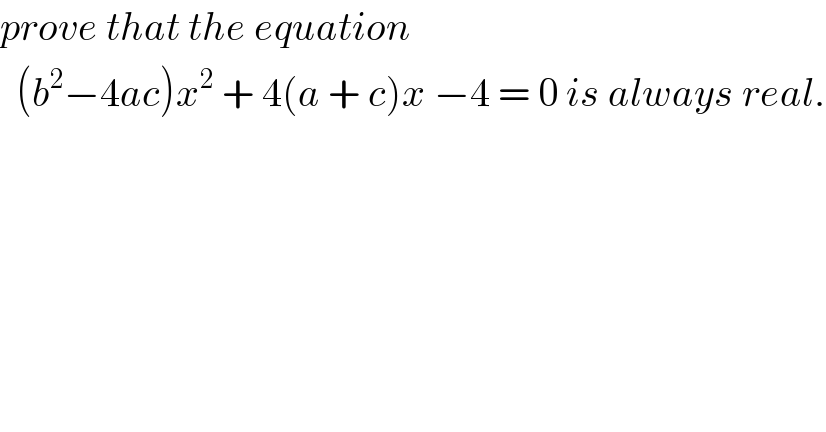
$${prove}\:{that}\:{the}\:{equation}\: \\ $$$$\:\:\left({b}^{\mathrm{2}} −\mathrm{4}{ac}\right){x}^{\mathrm{2}} \:+\:\mathrm{4}\left({a}\:+\:{c}\right){x}\:−\mathrm{4}\:=\:\mathrm{0}\:{is}\:{always}\:{real}. \\ $$
Commented by prakash jain last updated on 28/Sep/19
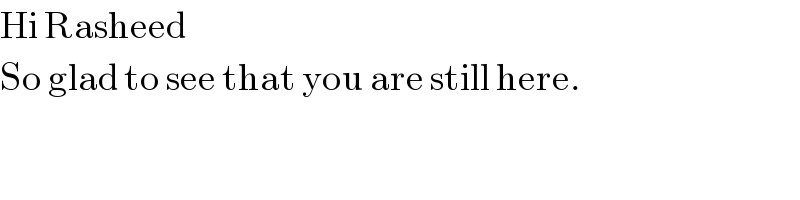
$$\mathrm{Hi}\:\mathrm{Rasheed} \\ $$$$\mathrm{So}\:\mathrm{glad}\:\mathrm{to}\:\mathrm{see}\:\mathrm{that}\:\mathrm{you}\:\mathrm{are}\:\mathrm{still}\:\mathrm{here}. \\ $$
Commented by prakash jain last updated on 27/Sep/19
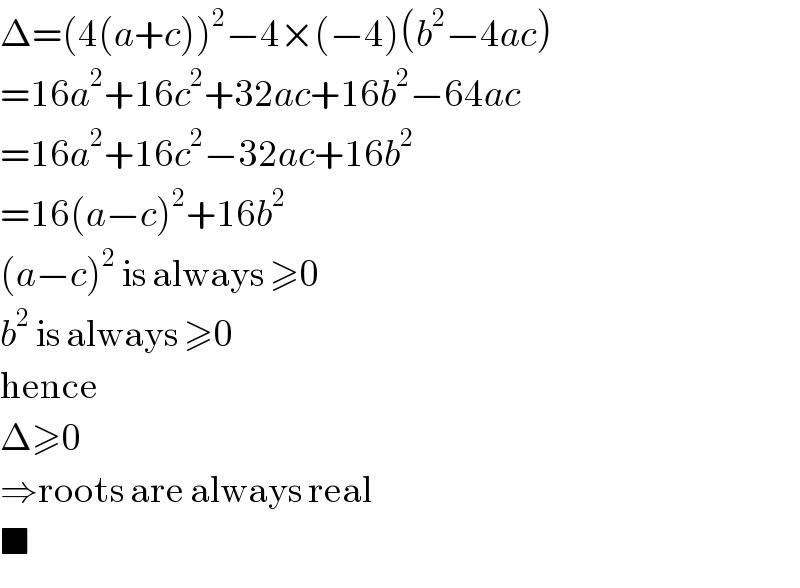
$$\Delta=\left(\mathrm{4}\left({a}+{c}\right)\right)^{\mathrm{2}} −\mathrm{4}×\left(−\mathrm{4}\right)\left({b}^{\mathrm{2}} −\mathrm{4}{ac}\right) \\ $$$$=\mathrm{16}{a}^{\mathrm{2}} +\mathrm{16}{c}^{\mathrm{2}} +\mathrm{32}{ac}+\mathrm{16}{b}^{\mathrm{2}} −\mathrm{64}{ac} \\ $$$$=\mathrm{16}{a}^{\mathrm{2}} +\mathrm{16}{c}^{\mathrm{2}} −\mathrm{32}{ac}+\mathrm{16}{b}^{\mathrm{2}} \\ $$$$=\mathrm{16}\left({a}−{c}\right)^{\mathrm{2}} +\mathrm{16}{b}^{\mathrm{2}} \\ $$$$\left({a}−{c}\right)^{\mathrm{2}} \:\mathrm{is}\:\mathrm{always}\:\geqslant\mathrm{0} \\ $$$${b}^{\mathrm{2}} \:\mathrm{is}\:\mathrm{always}\:\geqslant\mathrm{0} \\ $$$$\mathrm{hence} \\ $$$$\Delta\geqslant\mathrm{0} \\ $$$$\Rightarrow\mathrm{roots}\:\mathrm{are}\:\mathrm{always}\:\mathrm{real} \\ $$$$\blacksquare \\ $$
Commented by Abdo msup. last updated on 28/Sep/19

$${hello}\:{prakash}\:{you}\:{are}\:{absent}\:{for}\:{a}\:{long}\:{time}... \\ $$
Commented by Rasheed.Sindhi last updated on 28/Sep/19

$${Welcome}\:\boldsymbol{{sir}}\:\boldsymbol{{prakash}}.{Happy}\:{to}\:{see} \\ $$$${you}\:{in}\:{the}\:{forum}!\:{The}\:{forum}\:{needs}\:{you}. \\ $$
Commented by Rio Michael last updated on 28/Sep/19

$${thanks}\:{sir} \\ $$
Answered by mind is power last updated on 27/Sep/19

$${a}={b}={c}=\mathrm{0}\:{false} \\ $$$$ \\ $$
Commented by Rio Michael last updated on 27/Sep/19
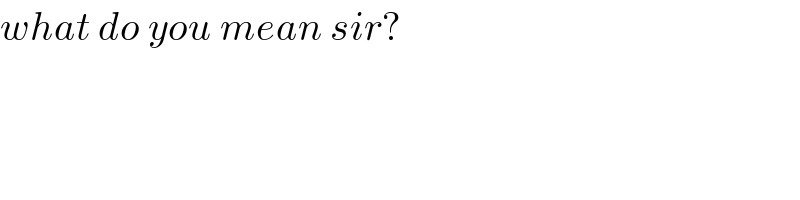
$${what}\:{do}\:{you}\:{mean}\:{sir}? \\ $$
Commented by mind is power last updated on 27/Sep/19
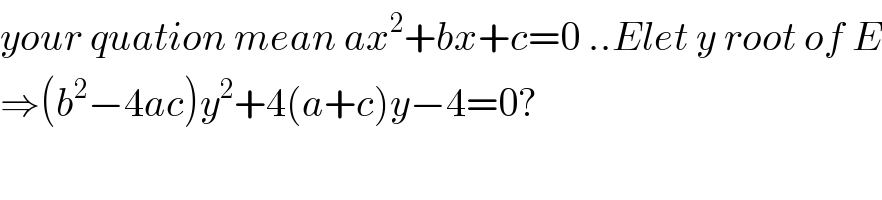
$${your}\:{quation}\:{mean}\:{ax}^{\mathrm{2}} +{bx}+{c}=\mathrm{0}\:..{Elet}\:{y}\:{root}\:{of}\:{E} \\ $$$$\Rightarrow\left({b}^{\mathrm{2}} −\mathrm{4}{ac}\right){y}^{\mathrm{2}} +\mathrm{4}\left({a}+{c}\right){y}−\mathrm{4}=\mathrm{0}? \\ $$
Commented by JDamian last updated on 28/Sep/19
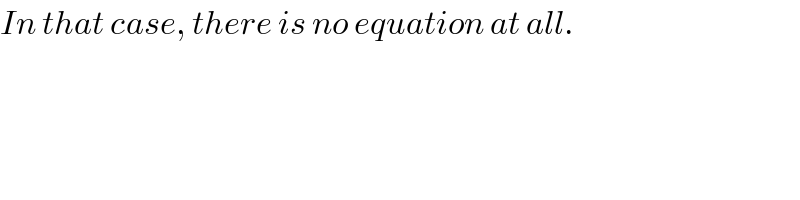
$${In}\:{that}\:{case},\:{there}\:{is}\:{no}\:{equation}\:{at}\:{all}. \\ $$
Answered by MJS last updated on 27/Sep/19

$$\mathrm{usually}\:\mathrm{when}\:\mathrm{dealing}\:\mathrm{with} \\ $$$${ax}^{\mathrm{2}} +{bx}+{c}=\mathrm{0} \\ $$$$\mathrm{it}\:\mathrm{is}\:\mathrm{clearly}\:\mathrm{implied}\:\mathrm{that}\:{a}\neq\mathrm{0} \\ $$$$\Rightarrow \\ $$$${x}^{\mathrm{2}} +\frac{\mathrm{4}\left({a}+{c}\right)}{{b}^{\mathrm{2}} −\mathrm{4}{ac}}{x}−\frac{\mathrm{4}}{{b}^{\mathrm{2}} −\mathrm{4}{ac}}=\mathrm{0};\:{a},\:{b},\:{c}\:\in\mathbb{R}\wedge{b}^{\mathrm{2}} −\mathrm{4}{ac}\neq\mathrm{0} \\ $$$${x}^{\mathrm{2}} +{px}+{q}=\mathrm{0}\:\Leftrightarrow\:{x}=−\frac{{p}}{\mathrm{2}}\pm\sqrt{\frac{{p}^{\mathrm{2}} }{\mathrm{4}}−{q}} \\ $$$$\mathrm{this}\:\mathrm{is}\:\mathrm{real}\:\mathrm{for}\:{D}=\frac{{p}^{\mathrm{2}} }{\mathrm{4}}−{q}\geqslant\mathrm{0} \\ $$$$\Rightarrow\:{D}=\mathrm{4}\frac{{a}^{\mathrm{2}} −\mathrm{2}{ac}+{b}^{\mathrm{2}} +{c}^{\mathrm{2}} }{\left({b}^{\mathrm{2}} −\mathrm{4}{ac}\right)^{\mathrm{2}} }=\mathrm{4}\frac{\left({a}−{c}\right)^{\mathrm{2}} +{b}^{\mathrm{2}} }{\left({b}^{\mathrm{2}} −\mathrm{4}{ac}\right)^{\mathrm{2}} }>\mathrm{0}\:\Rightarrow \\ $$$$\Rightarrow\:{x}\in\mathbb{R} \\ $$
Commented by Rio Michael last updated on 27/Sep/19

$${thank}\:{you}\:{sir} \\ $$
