
Question Number 69765 by Rio Michael last updated on 27/Sep/19
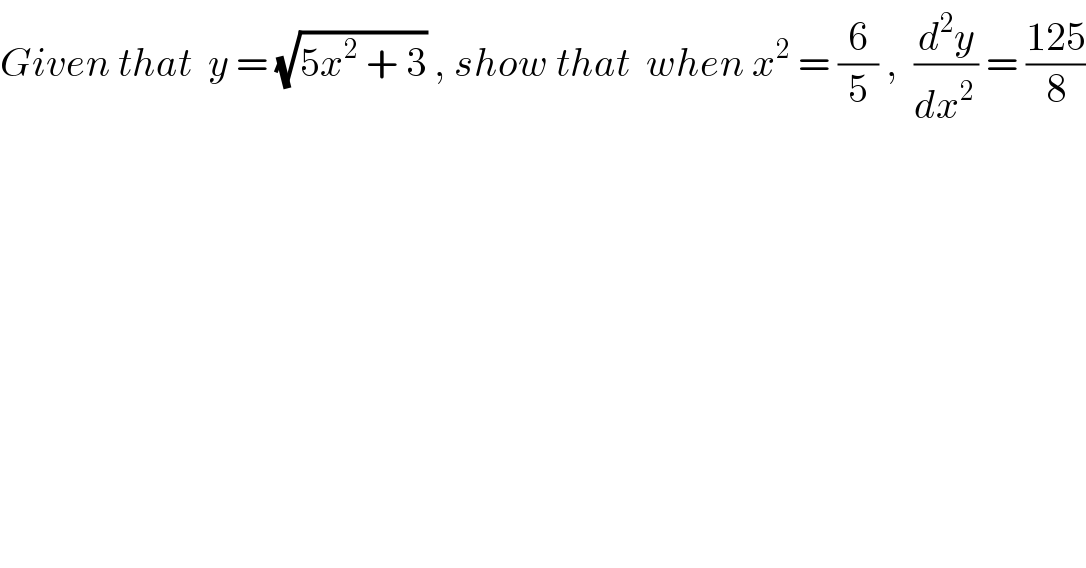
$${Given}\:{that}\:\:{y}\:=\:\sqrt{\mathrm{5}{x}^{\mathrm{2}} \:+\:\mathrm{3}}\:,\:{show}\:{that}\:\:{when}\:{x}^{\mathrm{2}} \:=\:\frac{\mathrm{6}}{\mathrm{5}}\:,\:\:\frac{{d}^{\mathrm{2}} {y}}{{dx}^{\mathrm{2}\:} }\:=\:\frac{\mathrm{125}}{\mathrm{8}} \\ $$
Answered by MJS last updated on 27/Sep/19
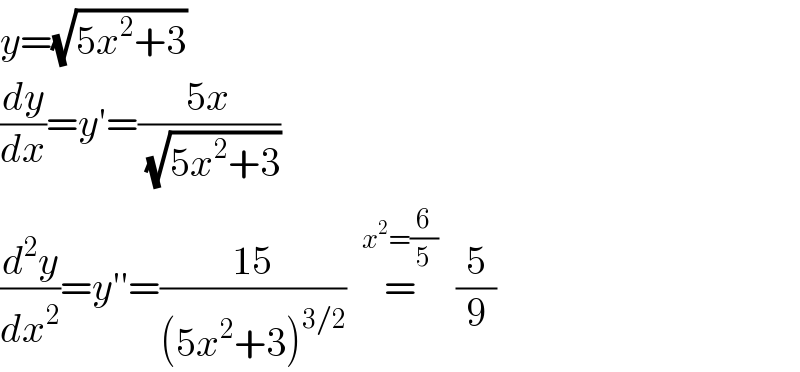
$${y}=\sqrt{\mathrm{5}{x}^{\mathrm{2}} +\mathrm{3}} \\ $$$$\frac{{dy}}{{dx}}={y}'=\frac{\mathrm{5}{x}}{\sqrt{\mathrm{5}{x}^{\mathrm{2}} +\mathrm{3}}} \\ $$$$\frac{{d}^{\mathrm{2}} {y}}{{dx}^{\mathrm{2}} }={y}''=\frac{\mathrm{15}}{\left(\mathrm{5}{x}^{\mathrm{2}} +\mathrm{3}\right)^{\mathrm{3}/\mathrm{2}} }\:\:\overset{{x}^{\mathrm{2}} =\frac{\mathrm{6}}{\mathrm{5}}} {=}\:\:\:\:\:\frac{\mathrm{5}}{\mathrm{9}} \\ $$
