
Question Number 69763 by Rio Michael last updated on 27/Sep/19
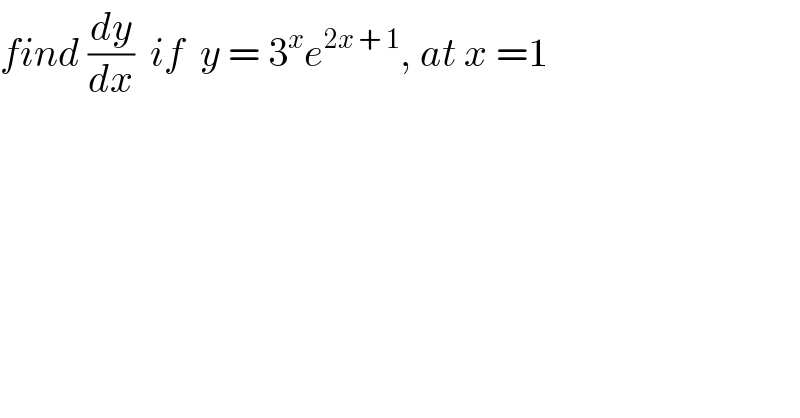
$${find}\:\frac{{dy}}{{dx}}\:\:{if}\:\:{y}\:=\:\mathrm{3}^{{x}} {e}^{\mathrm{2}{x}\:+\:\mathrm{1}} ,\:{at}\:{x}\:=\mathrm{1} \\ $$
Commented by mathmax by abdo last updated on 16/Oct/19
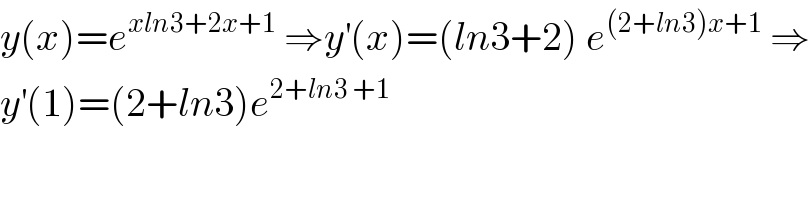
$${y}\left({x}\right)={e}^{{xln}\mathrm{3}+\mathrm{2}{x}+\mathrm{1}} \:\Rightarrow{y}^{'} \left({x}\right)=\left({ln}\mathrm{3}+\mathrm{2}\right)\:{e}^{\left(\mathrm{2}+{ln}\mathrm{3}\right){x}+\mathrm{1}} \:\Rightarrow \\ $$$${y}^{'} \left(\mathrm{1}\right)=\left(\mathrm{2}+{ln}\mathrm{3}\right){e}^{\mathrm{2}+{ln}\mathrm{3}\:+\mathrm{1}} \\ $$
Commented by $@ty@m123 last updated on 16/Oct/19

$${It}\:{has}\:{minor}\:{typo}\:{error}. \\ $$
Answered by $@ty@m123 last updated on 27/Sep/19
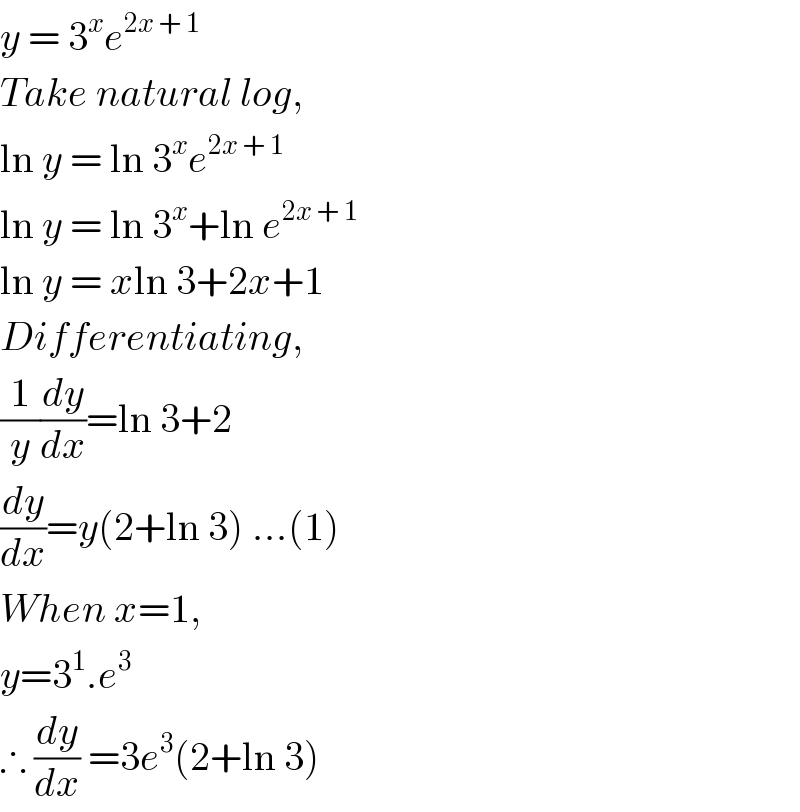
$${y}\:=\:\mathrm{3}^{{x}} {e}^{\mathrm{2}{x}\:+\:\mathrm{1}} \\ $$$${Take}\:{natural}\:{log}, \\ $$$$\mathrm{ln}\:{y}\:=\:\mathrm{ln}\:\mathrm{3}^{{x}} {e}^{\mathrm{2}{x}\:+\:\mathrm{1}} \\ $$$$\mathrm{ln}\:{y}\:=\:\mathrm{ln}\:\mathrm{3}^{{x}} +\mathrm{ln}\:{e}^{\mathrm{2}{x}\:+\:\mathrm{1}} \\ $$$$\mathrm{ln}\:{y}\:=\:{x}\mathrm{ln}\:\mathrm{3}+\mathrm{2}{x}+\mathrm{1} \\ $$$${Differentiating}, \\ $$$$\frac{\mathrm{1}}{{y}}\frac{{dy}}{{dx}}=\mathrm{ln}\:\mathrm{3}+\mathrm{2} \\ $$$$\frac{{dy}}{{dx}}={y}\left(\mathrm{2}+\mathrm{ln}\:\mathrm{3}\right)\:...\left(\mathrm{1}\right) \\ $$$${When}\:{x}=\mathrm{1}, \\ $$$${y}=\mathrm{3}^{\mathrm{1}} .{e}^{\mathrm{3}} \\ $$$$\therefore\:\frac{{dy}}{{dx}}\:=\mathrm{3}{e}^{\mathrm{3}} \left(\mathrm{2}+\mathrm{ln}\:\mathrm{3}\right) \\ $$
Commented by Rio Michael last updated on 27/Sep/19

$${thanks}\:{sir} \\ $$
