
Question Number 69662 by aliesam last updated on 26/Sep/19
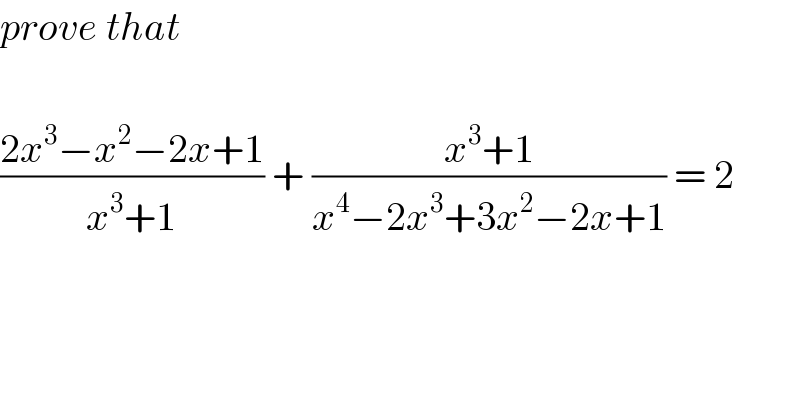
$${prove}\:{that} \\ $$$$ \\ $$$$\frac{\mathrm{2}{x}^{\mathrm{3}} −{x}^{\mathrm{2}} −\mathrm{2}{x}+\mathrm{1}}{{x}^{\mathrm{3}} +\mathrm{1}}\:+\:\frac{{x}^{\mathrm{3}} +\mathrm{1}}{{x}^{\mathrm{4}} −\mathrm{2}{x}^{\mathrm{3}} +\mathrm{3}{x}^{\mathrm{2}} −\mathrm{2}{x}+\mathrm{1}}\:=\:\mathrm{2} \\ $$
Answered by MJS last updated on 26/Sep/19
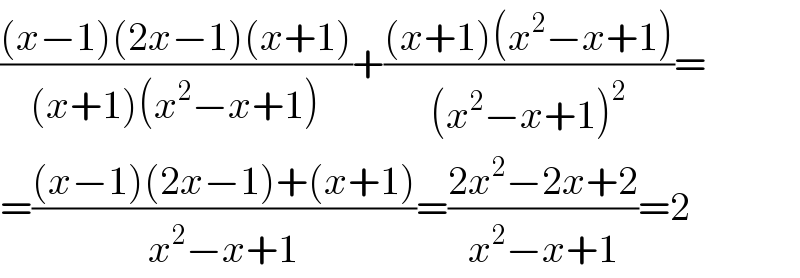
$$\frac{\left({x}−\mathrm{1}\right)\left(\mathrm{2}{x}−\mathrm{1}\right)\left({x}+\mathrm{1}\right)}{\left({x}+\mathrm{1}\right)\left({x}^{\mathrm{2}} −{x}+\mathrm{1}\right)}+\frac{\left({x}+\mathrm{1}\right)\left({x}^{\mathrm{2}} −{x}+\mathrm{1}\right)}{\left({x}^{\mathrm{2}} −{x}+\mathrm{1}\right)^{\mathrm{2}} }= \\ $$$$=\frac{\left({x}−\mathrm{1}\right)\left(\mathrm{2}{x}−\mathrm{1}\right)+\left({x}+\mathrm{1}\right)}{{x}^{\mathrm{2}} −{x}+\mathrm{1}}=\frac{\mathrm{2}{x}^{\mathrm{2}} −\mathrm{2}{x}+\mathrm{2}}{{x}^{\mathrm{2}} −{x}+\mathrm{1}}=\mathrm{2} \\ $$
Commented by aliesam last updated on 26/Sep/19

$${thank}\:{you}\:{sir}\: \\ $$
