
Question Number 69644 by ahmadshahhimat775@gmail.com last updated on 26/Sep/19
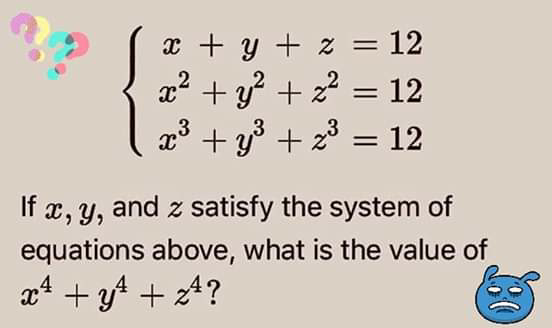
Answered by MJS last updated on 26/Sep/19
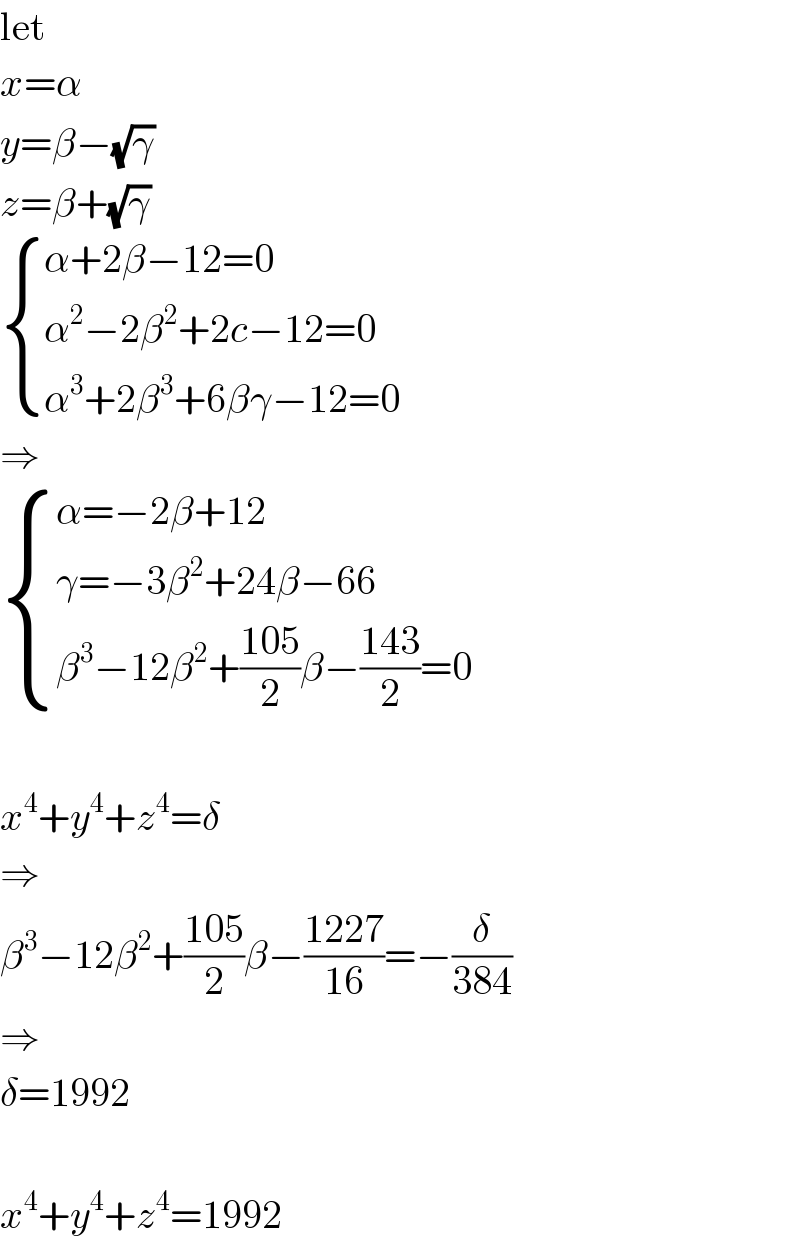
$$\mathrm{let} \\ $$$${x}=\alpha \\ $$$${y}=\beta−\sqrt{\gamma} \\ $$$${z}=\beta+\sqrt{\gamma} \\ $$$$\begin{cases}{\alpha+\mathrm{2}\beta−\mathrm{12}=\mathrm{0}}\\{\alpha^{\mathrm{2}} −\mathrm{2}\beta^{\mathrm{2}} +\mathrm{2}{c}−\mathrm{12}=\mathrm{0}}\\{\alpha^{\mathrm{3}} +\mathrm{2}\beta^{\mathrm{3}} +\mathrm{6}\beta\gamma−\mathrm{12}=\mathrm{0}}\end{cases} \\ $$$$\Rightarrow \\ $$$$\begin{cases}{\alpha=−\mathrm{2}\beta+\mathrm{12}}\\{\gamma=−\mathrm{3}\beta^{\mathrm{2}} +\mathrm{24}\beta−\mathrm{66}}\\{\beta^{\mathrm{3}} −\mathrm{12}\beta^{\mathrm{2}} +\frac{\mathrm{105}}{\mathrm{2}}\beta−\frac{\mathrm{143}}{\mathrm{2}}=\mathrm{0}}\end{cases} \\ $$$$ \\ $$$${x}^{\mathrm{4}} +{y}^{\mathrm{4}} +{z}^{\mathrm{4}} =\delta \\ $$$$\Rightarrow \\ $$$$\beta^{\mathrm{3}} −\mathrm{12}\beta^{\mathrm{2}} +\frac{\mathrm{105}}{\mathrm{2}}\beta−\frac{\mathrm{1227}}{\mathrm{16}}=−\frac{\delta}{\mathrm{384}} \\ $$$$\Rightarrow \\ $$$$\delta=\mathrm{1992} \\ $$$$ \\ $$$${x}^{\mathrm{4}} +{y}^{\mathrm{4}} +{z}^{\mathrm{4}} =\mathrm{1992} \\ $$
Commented by mind is power last updated on 26/Sep/19
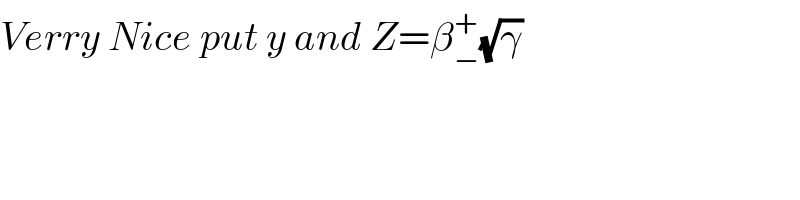
$${Verry}\:{Nice}\:{put}\:{y}\:{and}\:{Z}=\beta_{−} ^{+} \sqrt{\gamma} \\ $$$$ \\ $$
Answered by ajfour last updated on 26/Sep/19
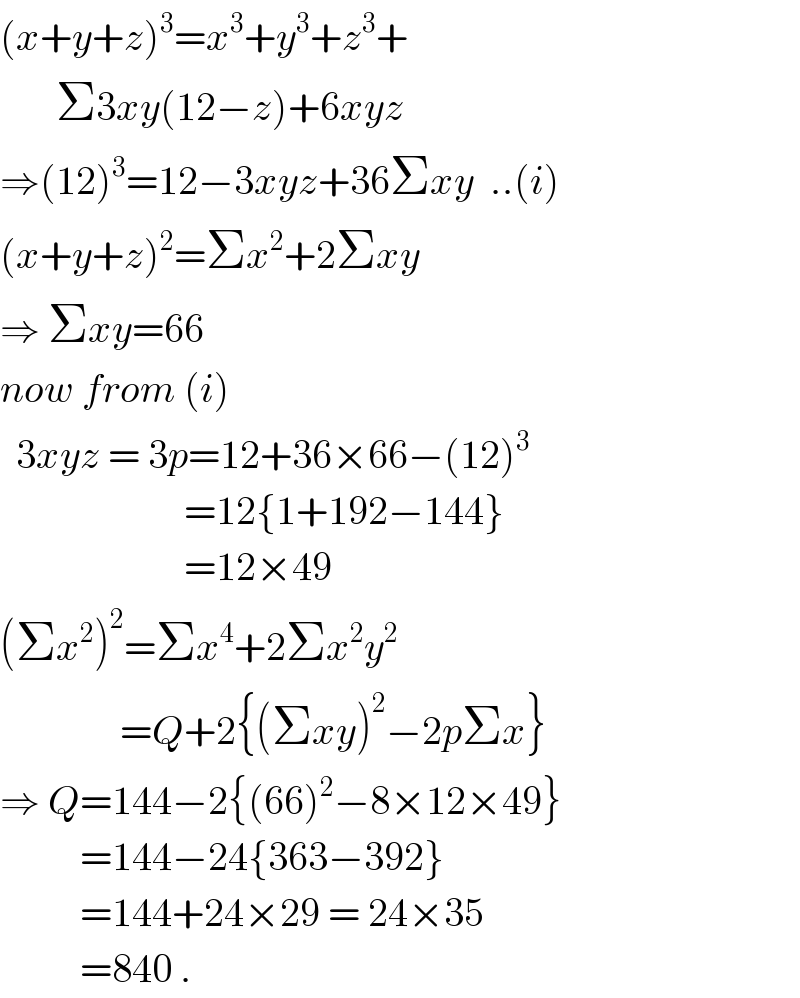
$$\left({x}+{y}+{z}\right)^{\mathrm{3}} ={x}^{\mathrm{3}} +{y}^{\mathrm{3}} +{z}^{\mathrm{3}} + \\ $$$$\:\:\:\:\:\:\:\Sigma\mathrm{3}{xy}\left(\mathrm{12}−{z}\right)+\mathrm{6}{xyz} \\ $$$$\Rightarrow\left(\mathrm{12}\right)^{\mathrm{3}} =\mathrm{12}−\mathrm{3}{xyz}+\mathrm{36}\Sigma{xy}\:\:..\left({i}\right) \\ $$$$\left({x}+{y}+{z}\right)^{\mathrm{2}} =\Sigma{x}^{\mathrm{2}} +\mathrm{2}\Sigma{xy} \\ $$$$\Rightarrow\:\Sigma{xy}=\mathrm{66} \\ $$$${now}\:{from}\:\left({i}\right) \\ $$$$\:\:\mathrm{3}{xyz}\:=\:\mathrm{3}{p}=\mathrm{12}+\mathrm{36}×\mathrm{66}−\left(\mathrm{12}\right)^{\mathrm{3}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{12}\left\{\mathrm{1}+\mathrm{192}−\mathrm{144}\right\} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{12}×\mathrm{49} \\ $$$$\left(\Sigma{x}^{\mathrm{2}} \right)^{\mathrm{2}} =\Sigma{x}^{\mathrm{4}} +\mathrm{2}\Sigma{x}^{\mathrm{2}} {y}^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:={Q}+\mathrm{2}\left\{\left(\Sigma{xy}\right)^{\mathrm{2}} −\mathrm{2}{p}\Sigma{x}\right\} \\ $$$$\Rightarrow\:{Q}=\mathrm{144}−\mathrm{2}\left\{\left(\mathrm{66}\right)^{\mathrm{2}} −\mathrm{8}×\mathrm{12}×\mathrm{49}\right\} \\ $$$$\:\:\:\:\:\:\:\:\:\:=\mathrm{144}−\mathrm{24}\left\{\mathrm{363}−\mathrm{392}\right\} \\ $$$$\:\:\:\:\:\:\:\:\:\:=\mathrm{144}+\mathrm{24}×\mathrm{29}\:=\:\mathrm{24}×\mathrm{35} \\ $$$$\:\:\:\:\:\:\:\:\:\:=\mathrm{840}\:. \\ $$
