
Question Number 69608 by TawaTawa last updated on 25/Sep/19
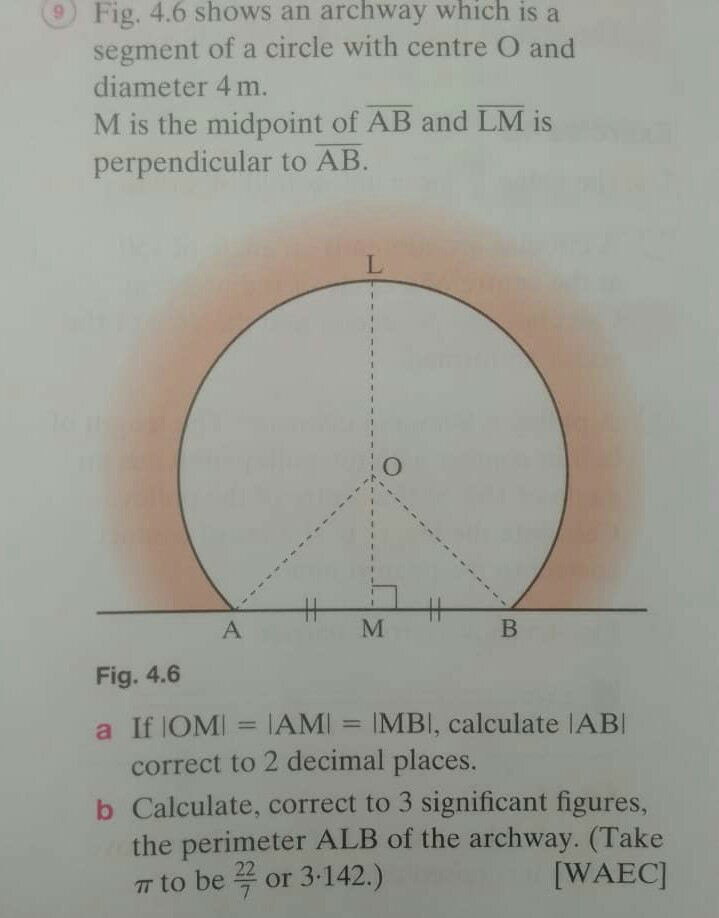
Commented by Prithwish sen last updated on 27/Sep/19
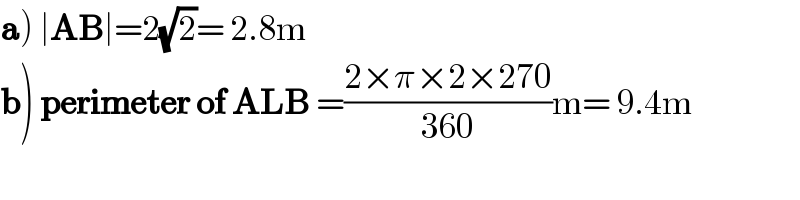
$$\left.\boldsymbol{\mathrm{a}}\right)\:\mid\boldsymbol{\mathrm{AB}}\mid=\mathrm{2}\sqrt{\mathrm{2}}=\:\mathrm{2}.\mathrm{8m} \\ $$$$\left.\boldsymbol{\mathrm{b}}\right)\:\boldsymbol{\mathrm{perimeter}}\:\boldsymbol{\mathrm{of}}\:\boldsymbol{\mathrm{ALB}}\:=\frac{\mathrm{2}×\pi×\mathrm{2}×\mathrm{270}}{\mathrm{360}}\mathrm{m}=\:\mathrm{9}.\mathrm{4m} \\ $$
Commented by TawaTawa last updated on 25/Sep/19
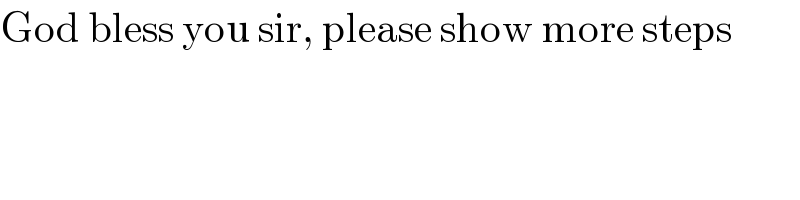
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir},\:\mathrm{please}\:\mathrm{show}\:\mathrm{more}\:\mathrm{steps} \\ $$
Answered by mind is power last updated on 25/Sep/19
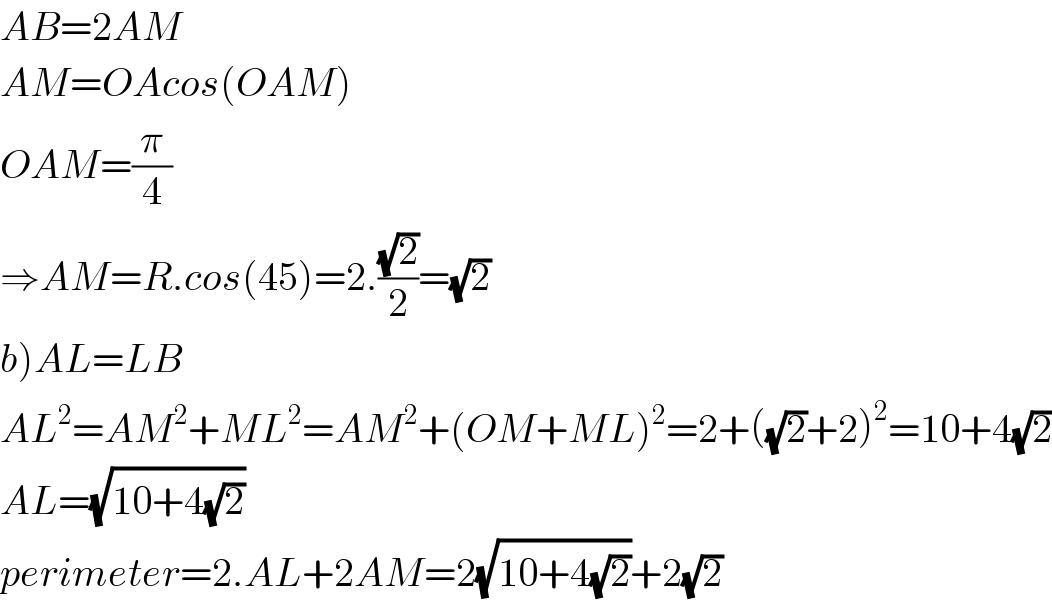
$${AB}=\mathrm{2}{AM} \\ $$$${AM}={OAcos}\left({OAM}\right) \\ $$$${OAM}=\frac{\pi}{\mathrm{4}} \\ $$$$\Rightarrow{AM}={R}.{cos}\left(\mathrm{45}\right)=\mathrm{2}.\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}=\sqrt{\mathrm{2}} \\ $$$$\left.{b}\right){AL}={LB} \\ $$$${AL}^{\mathrm{2}} ={AM}^{\mathrm{2}} +{ML}^{\mathrm{2}} ={AM}^{\mathrm{2}} +\left({OM}+{ML}\right)^{\mathrm{2}} =\mathrm{2}+\left(\sqrt{\mathrm{2}}+\mathrm{2}\right)^{\mathrm{2}} =\mathrm{10}+\mathrm{4}\sqrt{\mathrm{2}} \\ $$$${AL}=\sqrt{\mathrm{10}+\mathrm{4}\sqrt{\mathrm{2}}} \\ $$$${perimeter}=\mathrm{2}.{AL}+\mathrm{2}{AM}=\mathrm{2}\sqrt{\mathrm{10}+\mathrm{4}\sqrt{\mathrm{2}}}+\mathrm{2}\sqrt{\mathrm{2}} \\ $$
Commented by TawaTawa last updated on 25/Sep/19
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$
Commented by mind is power last updated on 26/Sep/19

$${y}'{re}\:{welcom} \\ $$
Commented by TawaTawa last updated on 26/Sep/19

$$\mathrm{Sir},\:\mathrm{please}\:\mathrm{help}\:\mathrm{me}\:\mathrm{check}.\:\mathrm{the}\:\mathrm{perimeter}\:\mathrm{here}\:\mathrm{is}\:\:\mathrm{9}.\mathrm{4}\:\:\mathrm{but}\:\mathrm{your}\:\mathrm{annswer} \\ $$$$\mathrm{is}\:\:\mathrm{10}.\mathrm{7} \\ $$
