
Question Number 69603 by Mikael last updated on 25/Sep/19
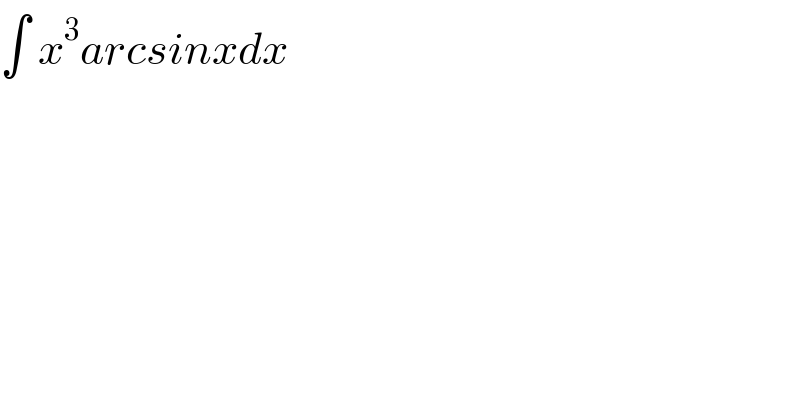
$$\int\:{x}^{\mathrm{3}} {arcsinxdx} \\ $$
Answered by MJS last updated on 25/Sep/19
![by parts ∫u′v=uv−∫uv′ u′=x^3 → u=(x^4 /4) v=arcsin x → v′=(1/(√(1−x^2 ))) ∫x^3 arcsin x dx=(x^4 /4)arcsin x −(1/4)∫(x^4 /(√(1−x^2 )))dx ∫(x^4 /(√(1−x^2 )))dx= [t=arcsin x → dx=(√(1−x^2 ))dt] =∫sin^4 t dt=(1/8)∫cos 4t dt −(1/2)∫cos 2t dt+(3/8)∫dt= =(1/(32))sin 4t −(1/4)sin 2t +(3/8)t= =−((1/4)x^3 −(3/8)x)(√(1−x^2 ))+(3/8)arcsin x ∫x^3 arcsin x dx=((1/4)x^4 −(3/(32)))arcsin x +(1/(32))x(2x^2 +3)(√(1−x^2 ))+C](Q69605.png)
$$\mathrm{by}\:\mathrm{parts} \\ $$$$\int{u}'{v}={uv}−\int{uv}' \\ $$$${u}'={x}^{\mathrm{3}} \:\rightarrow\:{u}=\frac{{x}^{\mathrm{4}} }{\mathrm{4}} \\ $$$${v}=\mathrm{arcsin}\:{x}\:\rightarrow\:{v}'=\frac{\mathrm{1}}{\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }} \\ $$$$\int{x}^{\mathrm{3}} \mathrm{arcsin}\:{x}\:{dx}=\frac{{x}^{\mathrm{4}} }{\mathrm{4}}\mathrm{arcsin}\:{x}\:−\frac{\mathrm{1}}{\mathrm{4}}\int\frac{{x}^{\mathrm{4}} }{\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}{dx} \\ $$$$\int\frac{{x}^{\mathrm{4}} }{\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}{dx}= \\ $$$$\:\:\:\:\:\left[{t}=\mathrm{arcsin}\:{x}\:\rightarrow\:{dx}=\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }{dt}\right] \\ $$$$=\int\mathrm{sin}^{\mathrm{4}} \:{t}\:{dt}=\frac{\mathrm{1}}{\mathrm{8}}\int\mathrm{cos}\:\mathrm{4}{t}\:{dt}\:−\frac{\mathrm{1}}{\mathrm{2}}\int\mathrm{cos}\:\mathrm{2}{t}\:{dt}+\frac{\mathrm{3}}{\mathrm{8}}\int{dt}= \\ $$$$=\frac{\mathrm{1}}{\mathrm{32}}\mathrm{sin}\:\mathrm{4}{t}\:−\frac{\mathrm{1}}{\mathrm{4}}\mathrm{sin}\:\mathrm{2}{t}\:+\frac{\mathrm{3}}{\mathrm{8}}{t}= \\ $$$$=−\left(\frac{\mathrm{1}}{\mathrm{4}}{x}^{\mathrm{3}} −\frac{\mathrm{3}}{\mathrm{8}}{x}\right)\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }+\frac{\mathrm{3}}{\mathrm{8}}\mathrm{arcsin}\:{x} \\ $$$$ \\ $$$$\int{x}^{\mathrm{3}} \mathrm{arcsin}\:{x}\:{dx}=\left(\frac{\mathrm{1}}{\mathrm{4}}{x}^{\mathrm{4}} −\frac{\mathrm{3}}{\mathrm{32}}\right)\mathrm{arcsin}\:{x}\:+\frac{\mathrm{1}}{\mathrm{32}}{x}\left(\mathrm{2}{x}^{\mathrm{2}} +\mathrm{3}\right)\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }+{C} \\ $$
Commented by Mikaell last updated on 27/Sep/19
$${great}\:{Sir}.\:{thank}\:{you}. \\ $$
